Les ondes stationnaires sphériques.

Il s'agit d'un électron, qui possède la propriété remarquable de se déplacer grâce à l'effet Doppler.

L'électron est une onde.

Cette étude affirme que la matière est faite exclusivement d'ondes stationnaires sphériques et que l'univers matériel est composé uniquement d'éther. Cela confirme et explique les prévisions de Lorentz, qui conduisent à la Relativité.

Si vous possédez un minimum de sens critique, vous devriez penser que ces affirmations sont suspectes. Mais d'un autre côté vous devriez admettre que malgré toutes les découvertes de la physique, la mécanique de la matière nous échappe encore totalement. Par exemple, personne n'a jamais décrit l'électron d'une manière précise.

Devant l'inconnu, il nous faut élaborer des hypothèses et les évaluer.

Un domaine ignoré et méprisé.

Ne cherchez pas de renseignements sur l'Internet à propos des ondes stationnaires sphériques. Il est probable que vous ne trouverez que mes propres pages. Ces ondes ont certainement été étudiées par quelques physiciens, mais je n'ai jamais réussi à en retracer un seul, sauf bien entendu M. Milo Wolff que j'ai cité plus haut. Il semble bien qu'il s'agisse de l'un des domaines les plus ignorés et méprisés de toute la physique.

Cette attitude est incompréhensible. Des milliers de spécialistes en physique nucléaire savent que la matière possède des propriétés ondulatoires. Les ondes planes étant tout à fait exclues, il ne peut s'agir que d'ondes sphériques ; et comme l'a si bien écrit Louis de Broglie, ce sont sans doute des ondes stationnaires. De plus la mobilité de la matière suggère fortement que ces ondes devraient subir l'effet Doppler.

Ce cheminement est élémentaire. Il devrait inciter les scientifiques à étudier plus à fond les propriétés des ondes stationnaires sphériques. Et pourtant ils négligent complètement cette avenue. Ils la méprisent même. Pourtant on pourrait facilement vérifier au moyen d'expériences relativement simples que les ondes stationnaires sphériques présentent toutes les propriétés de l'électron.

On peut même faire mieux, car depuis l'invention d'un médium informatique par M. Philippe Delmotte en juin 2005, ces ondes peuvent maintenant être vérifiées de manière virtuelle. Mais là encore, cette invention tarde à être reconnue, même si les opticiens et les acousticiens en particulier pourraient en bénéficier largement.

LES ONDES STATIONNAIRES CIRCULAIRES

Avant d'aborder les ondes stationnaires sphériques, il serait utile de rappeler qu'il existe aussi des ondes stationnaires circulaires. Les "ronds dans l'eau" obtenus à l'aide d'un grand cerceau en sont un bon exemple, mais leurs propriétés sont différentes. On peut obtenir des ondes stationnaires circulaires sonores entre deux disques espacés d'une fraction de longueur d'onde seulement. On pourrait même en faire un jeu d'orgue au timbre très particulier, puisque le ventre central mesure trois-quarts d'onde. Il en résulterait des harmoniques très inhabituels puisque la taille de ce ventre varie avec la fréquence !

Grâce au principe de Huygens, j'ai pu retracer la configuration de ces ondes stationnaires circulaires. Je répète que le diamètre du noyau central mesure trois-quarts d'onde, et non l'onde entière des ondes sphériques :

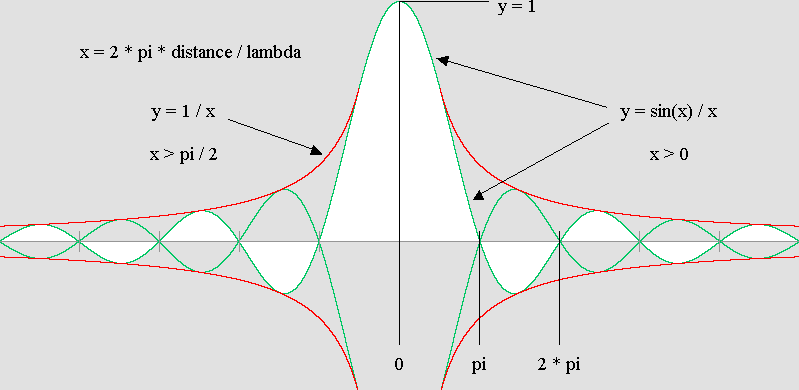
Les ondes stationnaires circulaires. Le diamètre du noyau central mesure trois-quarts d'onde.

La distance « x » est exprimée en radians : x = 2 * pi * distance / lambda

L'amplitude « y » des sinusoïdes vaut approximativement, avec avec x > pi / 3 :

y = sin(x + pi / 4) / (Sqr(x * pi / 2))

L'amplitude générale des ondes décroît avec la distance selon :

y = 1 / Sqr(x * pi / 2))

L'amplitude au centre du noyau (le lobe central ci-dessus) étant normalisée à 1, la variable y désigne l'amplitude comparativement à ce centre selon la distance « x » exprimée en radians. Grâce au programme Ether06.exe Ether06.bas, j'ai déjà pu vérifier que cette configuration est correcte.

Qu'il s'agisse des ondes circulaires progressives ou stationnaires, ce programme en montre tous les aspects. Il faut souligner qu'il utilise mon algorithme sur la tache d'Airy en effectuant la sommation d'un grand nombre d'ondelettes de Huygens. Je remercie chaleureusement M. Jocelyn Marcotte d'avoir accéléré les calculs en obtenant toutes les étapes d'une période à l'aide de deux résultats seulement, soit la phase et la quadrature.

Pour peu que je sache, ces renseignements pourtant élémentaires ne sont disponibles nulle part. Je rêve naïvement que je pourrais avoir été le premier à les rendre publics, soit en septembre 2005, mais c'est très improbable.

Il faut noter que l'amplitude est inversement proportionnelle à la racine carrée de la distance. Mes premières vérifications à l'aide du médium virtuel de M. Delmotte montrent que si l'effet Doppler intervient, l'amplitude des ondes est la même vers l'avant et vers l'arrière pour une distance donnée. C'est vrai aussi dans un système en trois dimensions, le rapport des amplitudes avant et arrière valant : R = (1+bêta)/(1–bêta) pour une même onde sphérique. Mais dans le cas des ondes circulaires, puisque l'amplitude est inversement proportionnelle à la racine carrée de la distance, ce rapport vaut plutôt :

R = Sqr( (1 + bêta) / (1 – bêta) )

LES ONDES PROGRESSIVES SPHÉRIQUES

On sait depuis longtemps que l'amplitude des ondes sphériques est inversement proportionnelle à la distance au centre. L'énergie valant le carré de l'amplitude, elle est donc inversement proportionnelle au carré de la distance.

En réalité, ce n'est pas si simple. La raison véritable de ce comportement, c'est que le médium dans lequel les ondes se déploient doit subir une compression puis une dilatation à chaque cycle. Or ces modifications ne peuvent s'étendre au-delà d'une demi-longueur d'onde. L'énergie que transmet chaque front d'onde est répartie d'une manière sinusoïdale dans une sorte de « couche d'oignon » sphérique dont le volume « v » correspond au grand rayon moins le petit rayon. On sait que le volume « V » d'une sphère vaut :

V = 4 * pi * r ^ 3 / 3

C'est donc le volume v de la couche, qui près du centre ne correspond pas exactement à sa distance, qui détermine de façon précise la courbe générale d'amplitude des ondes sphériques. C'est donc au voisinage du centre que la différence devient évidente, car autrement l'amplitude devrait être infinie comme l'indique la courbe bleue (y = 1 / x) sur cette animation :

Le programme generateur_d_ondes_spheriques.bas generateur_d_ondes_spheriques.exe qui a produit ces images ne montre qu'une courbe approchée (c'est la courbe noire selon y = 1 / v). Le volume v doit être normalisé à 1 au centre, soit avec x = 0. Le calcul utilisé est discutable mais efficace, car autrement il faudrait effectuer la sommation des couches successives selon une distribution sinusoïdale. J'ai échoué en tentant d'effectuer une sommation sinusoïdale simple, ce qui indique que la répartition est plus complexe que prévu. J'ai de bonnes raisons de penser qu'une répartition selon la distribution normale y = pi ^ (–x ^ 2) donnerait des résultats encore plus précis. Je lance donc un défi aux mathématiciens de trouver la formule élémentaire v = ? qui indique le volume de la couche d'oignon selon la distance du centre (selon l'analogie de M. Milo Wolff) et qui manque à cette étude.

Le générateur Marcotte.

En ce qui concerne la période de l'onde au voisinage du centre, j'ai réussi à mettre au point en mai 2007 une formule qui tienne compte de la réflexion dure, qui se traduit par des ondes qui se superposent en opposition de phase (je dois préciser ici que c'est M. Jocelyn Marcotte qui m'a informé de ce comportement en observant des ondes convergentes dans le médium virtuel de son invention). Lorsque x est inférieur à pi, une partie de la moitié intérieure de la couche dont dépend v devient négative, et il faut alors postuler qu'elle est réfléchie en opposition de phase. Il se produit finalement un retard de phase d'un quart de période (pi / 2) au centre, d'où une correction progressive valant :

correction = (pi / 2) * (1 – x / pi) ^ 2

Je crois utile de signaler que les radioélectriciens parlent parfois d'une "sphère de Poynting" entourant une antenne d'émission. Ils font valoir que les champs au voisinage de cette antenne ont pour effet de produire de la self-induction, d'où une "réactance" qui fait en sorte que la période au voisinage de l'antenne est finalement modifiée d'une manière semblable.

Le calcul du volume v de chaque "couche d'oignon" se révélant plus complexe que prévu, j'ai dû me rabattre sur une autre approche pour montrer le comportement d'un émetteur d'ondes progressives. Dans ce cas particulier, l'amplitude dans la sphère intérieure n'est pas nécessairement celle de l'électron, puisque l'énergie (distribuée idéalement d'une manière sinusoïdale) s'échappe progressivement sans rencontrer d'opposition au premier nœud d'amplitude. Puisqu'il n'y a pas d'ondes stationnaires, ce nœud n'existe plus.

J'ai donc cherché comment exprimer le tout au moyen d'une formule simple et ce n'est que le 26 septembre 2007 que j'ai réalisé que la correction indiquée ci-dessus pouvait être appliquée à la variable x dans le cas où elle était inférieure à pi.

Le programme « Le Générateur d'Ondes Marcotte ».

Voici comment le programme peut afficher ces ondes. La période vaut :

x = 2 * pi * distance / lambda

La variable x représente plus exactement le délai en raison de la distance, en radians. Toutefois, il faut appliquer la correction indiquée plus haut si ce délai est inférieur à pi. Le but est de simuler la manière dont l'électron émet ses ondes, sachant qu'il présente un retard de phase de pi / 2 en son centre et que son noyau émetteur mesure une onde entière de diamètre. Cette particularité est capitale. En langage Basic ou FreeBasic, cela se traduit par l'instruction suivante:

If x < pi Then x = x + (pi / 2) * (1 – x / pi) ^ 2

Non seulement la période au centre s'en trouvera corrigée, mais la courbe obtenue sera étonnamment fluide et esthétique.

J'ai donné le nom de M. Jocelyn Marcotte à ce générateur d'ondes sphériques. En effet, c'est lui qui a découvert en mars 2006 que la formule bien connue sin(x) / x correspondait aux ondes stationnaires de l'électron. Il en a même fait la preuve à l'aide de son médium virtuel informatique en 3-D. Sa formule est remarquablement simple et elle fonctionne ici n'importe où sur la courbe, du centre à l'infini. Il suffit de lui ajouter un temps t pour obtenir une rotation :

t = 2 * pi * No. de l'image / nombre d'images par cycle

y = sin (x – t) / x

Bien sûr, il faut prévoir la singularité si x = 0. Alors a y = 1 ou sin(–t). Voici le programme qui le démontre (je regrette qu'il soit en anglais, mais je dois me tourner du côté anglophone puisque vous persistez à bouder mes découvertes !) :

Marcotte_Wave_Generator.bas Marcotte_Wave_Generator.exe

Le générateur d'ondes sphériques Marcotte.

Remarquez comment les ondes sont déportées au centre d'une distance additionnelle valant lambda / 4.

C'est la règle dans le cas de l'électron.

Le réseau d'interférences entre deux électrons ou positrons se transforme en puissant champ de force, car il est fait d'ondes stationnaires qui sont à leur tour amplifiées par les ondes de l'éther, de la même manière que celles de l'électron. Ce réseau doit être reproduit en tenant compte non seulement de la distance, mais aussi des deux spins et donc des quatre phases propres aux électrons et aux positrons. Mais surtout, il est capital d'ajouter le quart d'onde indiqué ci-dessus.

Le champ de force « biconvexe » est fait d'ondes stationnaires hyperboliques-elliptiques.

Chaque section ressemble à la lentille diffractive et devrait donc produire une tache d'Airy de part et d'autre.

La période sur l'axe varie en fonction de la distance et du spin des deux particules impliquées.

Rappelons que la correction de phase au centre éloigne chaque onde sphérique d'une distance additionnelle valant un quart d'onde. C'est capital ici, car au moment où ces ondes se rencontrent, leur période et donc celle du champ de force qui en résulte en est également affectée.

La moitié de l'énergie générée par leur amplification se traduit par un faisceau d'ondes convergentes qui est retourné vers les électrons ou les positrons qui leur ont donné naissance. J'ai déjà pu vérifier au moyen du principe de Huygens que ce faisceau convergent devrait produire une figure d'Airy sur le plan focal, mais aussi la diffraction de Fresnel qui lui est associée partout dans les environs. On sait que seuls, les faisceaux apodisés ne produisent pas la tache d'Airy classique (les anneaux sont absents), mais ce n'est pas le cas ici.

Par ailleurs, si les électrons sont très près l'un de l'autre, même leurs ondes stationnaires (et pas seulement les ondes qu'ils émettent) se composent. Alors les parties du champ de force situées au-delà d'eux se mettent à rayonner une tache d'Airy exactement au centre de l'axe qui les unit, ce qui produit un puissant champ gluonique, c'est à dire un quark dans lequel des électrons ou des positrons se dissimulent.

Le point important, c'est que la période des ondes du champ de force, sur l'axe, explique comment la pression de radiation agit. C'est pourquoi il était capital de trouver un générateur d'ondes qui reproduise le comportement de l'électron, sans aucun doute le plus parfait des générateurs d'ondes sphériques. Il sera très utiles aux chercheurs qui s'intéressent à la mécanique de la matière, mais aussi à ceux qui voudront imiter des vagues en travaillant sur des animations générées par ordinateur. Il sera même utile pour des tas d'autres applications !

Le programme suivant affiche des vagues artificielles en 3-D. C'est spectaculaire !

Marcotte_Wave_Generator_3D.bas Marcotte_Wave_Generator_3D.exe

Les ondes stationnaires sphériques.

Dans le cas des ondes stationnaires sphériques, le diamètre du noyau central fait une onde entière et non la demi-onde normale des « ventres » des ondes stationnaires planes. Il s'agit donc d'un ventre tout à fait particulier. Il y a inversion de phase par ajout d'une demi-longueur d'onde d'un côté à l'autre de ce noyau, ce qu'il fallait justifier.

L'animation d'un électron montrée plus haut a été réalisée par ordinateur en appliquant le principe de Huygens et elle montre pourquoi ce phénomène se produit. On présume que des milliers d'ondelettes de Huygens sont émises à partir de la surface interne d'une très grande sphère, puis on évalue de quelle manière elles se composent près du centre. Si les ondelettes proviennent d'une moitié seulement de la sphère, on obtient l'équivalent d'une tache d'Airy à pleine ouverture, soit sur 180°.

Si vous souhaitez étudier cette tache d'Airy, vous pouvez télécharger mon programme Ether16.exe Ether16.bas, qui en montre tous les aspects, l'angle d'ouverture pouvant atteindre 360°. Alors les ondelettes proviennent de la sphère en entier et l'on obtient plutôt des ondes stationnaires sphériques et concentriques, telles que décrites dans cette page.

On constate que les ondes progressives qui traversent (théoriquement) le noyau central rencontrent alternativement, à chaque demi-période, une zone comprimée puis dilatée. C'est pourquoi les ondes sont déportées alternativement dans la zone positive puis dans la zone négative, en haut puis en bas de l'axe horizontal. Cette pression et cette dilatation sont causées par les ondelettes de Huygens qui proviennent des directions transversales.

Ainsi, le passage d'une zone à l'autre a pour effet d'ajouter une demi-onde à la période, ce qui explique parfaitement pourquoi le noyau central d'un électron fait une onde entière et non pas la demi-onde normale des ventres des ondes stationnaires. Même si c'est difficile à croire, on constate que la vitesse des ondes, au moment précis où elles traversent le centre, est deux fois plus rapide que la vitesse de la lumière. D'ailleurs, ce phénomène s'observe aussi de part et d'autre de la tache d'Airy, mais dans une moindre mesure ; j'ose donc présumer que c'est un phénomène connu.

On en conclut que si les ondes provenant de deux électrons voisins sont en phase si elles se situent entre eux, elles seront en opposition de phase au-delà d'eux, et vice versa. Cette particularité est capitale et elle permettra de mieux expliquer leur comportement mutuel. Elle a un effet décisif sur la mécanique ondulatoire.

Une enveloppe caractéristique.

Le tableau suivant montre qu'on peut calculer très simplement l'amplitude relative des ondes stationnaires sphériques, et leur "enveloppe" caractéristique. Comme on l'a dit plus haut à propos des ondes sphériques, la courbe générale d'amplitude devrait être non pas y = 1 / x, mais plutôt y = 1 / v en tenant compte du volume v d'une couche sphérique du médium où l'onde peut se déployer. Malheureusement, ce volume est difficile à calculer.

La structure des ondes stationnaires sphériques.

En juillet 2006, M. Jocelyn Marcotte a réussi à établir les formules complètes qui permettent de reproduire les ondes stationnaires sphériques, et donc l'électron. Auparavant, je devais recourir au principe de Huygens, ce qui requiert des calculs longs et complexes. En particulier, la mise en place d'un électron dans un médium informatique en trois dimensions sera beaucoup plus simple et rapide. Il s'agit d'une découverte de la plus haute importance. Ci-dessous, la variable x doit être exprimée en radians selon x = 2 * pi * distance / lambda :

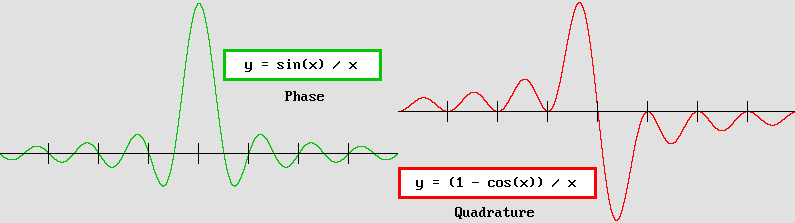
Les formules de M. Jocelyn Marcotte et les courbes correspondantes.

En fusionnant les deux équations et en introduisant un temps t, on peut réaliser une rotation complète :

y = (cos(t) * sin(x) – sin(t) * (1 – cos(x) ) ) / x

M. Philippe Delmotte a trouvé la simplification suivante en septembre 2006 :

y = (sin(t + x) – sin(t) ) / x

L'effet Doppler.

On a montré à la page d'accueil que, dans le but de provoquer un effet Doppler dans les ondes convergentes, il faudrait déplacer à vitesse constante un cerceau en forme d'ellipsoïde aplati tout en provoquant des ondulation de manière à respecter les transformations de Lorentz. Alors les vagues convergentes culminent au centre et sont ensuite réfléchies de manière à produire cette onde extraordinaire, qui n'est plus stationnaire :

Les ondes stationnaires sphériques non concentriques (v = 0,5 c).

C'est « l'Onde de LaFrenière » : l'électron est maintenant mobile.

Ce système se déplace vers la droite. Vous devez donc considérer que vous le suivez à la même vitesse.


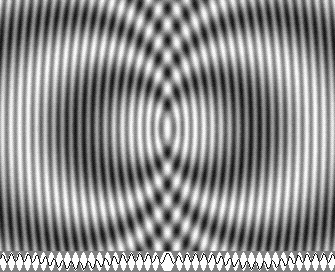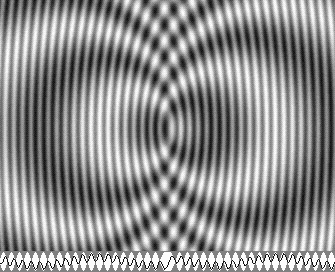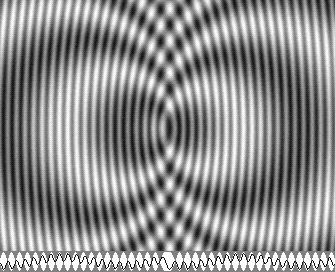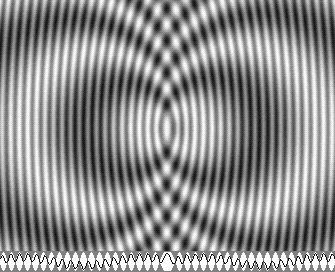v = 0,5 c	v = 0,866 c

Voici deux animations montrant l'onde à 50 % (à gauche) et à 86,6 % (à droite) de la vitesse de la lumière.

Ci-dessus, la vitesse de l'onde augmente à chaque image.

La contraction des ondes stationnaires sur l'axe est évidente.

Notez aussi que l'effet Doppler vers l'avant et vers l'arrière est étonnamment réciproque :

lambda ' = 1 / lambda


v = 0 c	v = 0,1 c

À gauche, l'onde est au repos. À droite, elle avance à 10 % de la vitesse de la lumière.

À faible vitesse, les inversions de phase selon l'équation du temps de Lorentz sont très perceptibles.

Elles produisent des bandes verticales qui défilent vers la droite à la vitesse de c / bêta longueurs d'ondes par période.

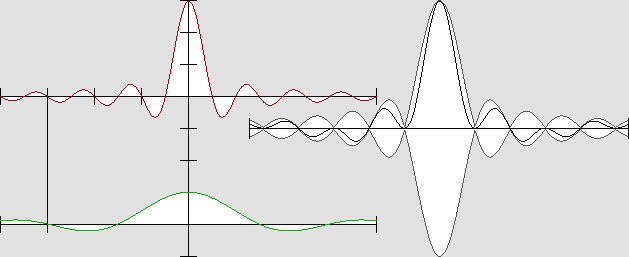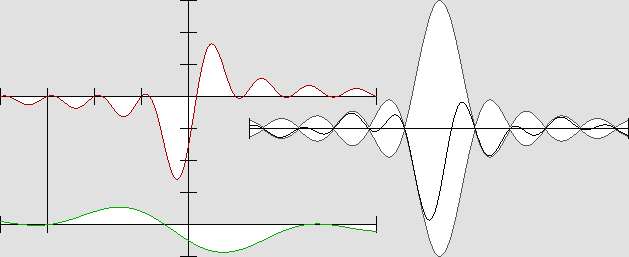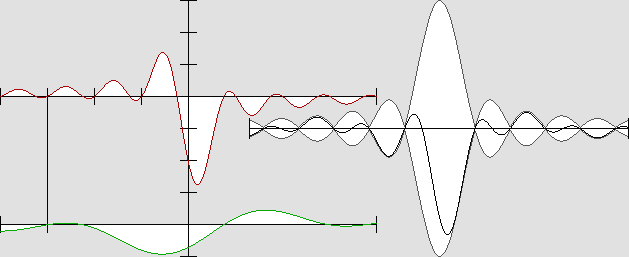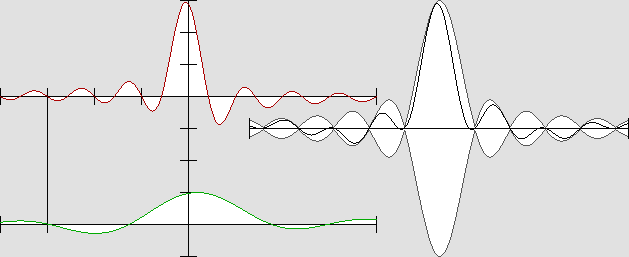
L'onde « stationnaire mobile », ou pseudo-stationnaire, lorsque v = 0,5 c.

Sur l'axe du déplacement, elle conserve l'enveloppe caractéristique qu'elle présentait au repos.

On peut alors parler d'ondes "stationnaires mobiles". À la différence des vagues, cette onde s'étend plutôt dans un espace en trois dimensions. Elle est toujours faite d'ondes sphériques, mais celles-ci ne sont plus concentriques à cause de l'effet Doppler. Elle est représentée ici dans son système de référence mobile, là où sa vitesse relative est nulle. Mais en fait elle est hautement mobile et sa vitesse ou sa direction peuvent varier.

Trois types d'ondes.

L'animation ci-dessous montre à quoi devrait ressembler un électron au repos. Près du noyau, l'intensité des ondes convergentes et divergentes est la même. Il s'agit véritablement d'ondes stationnaires. Un peu plus loin, à cause d'un phénomène d'amplification, l'intensité des ondes divergentes devient supérieure. On parle alors d'ondes partiellement stationnaires. Et enfin, beaucoup plus loin, les ondes sont uniquement divergentes. Ce sont des ondes simples ordinaires, dites progressives. La transition entre ces trois types peut se faire graduellement, et c'est effectivement ce qui se passe dans le cas d'un électron :

L'électron présente trois types d'ondes, selon la distance du centre.

Ses ondes stationnaires sont limitées à un faible espace : elles ne s'étendent pas à l'infini.

Les ondes stationnaires sphériques théoriques ne présentent pas cette particularité.

La science des ondes.

Cette étude affirme que la matière est faite d'ondes stationnaires. Pour y comprendre quelque chose, il est donc essentiel de bien connaître les ondes stationnaires. Et il ne faut pas les étudier longtemps pour réaliser que dans la plupart des cas, ces ondes ne sont pas stationnaires. Leur nom est très mal choisi car il prête à confusion.

En principe les ondes stationnaires résultent de la superposition de deux trains d'ondes progressives circulant en sens opposé. D'un point de vue mathématique, c'est très commode pour en expliquer le fonctionnement, et d'ailleurs je ne m'en prive pas moi-même. Mais il faut avoir très clairement à l'esprit que dans les faits, il s'agit d'une structure ondulatoire complètement différente. Un tel système n'a rien à voir avec les ondes progressives.

Par exemple, on peut considérer que les ondes progressives convergentes traversent le noyau central et deviennent alors divergentes. Mais on peut tout aussi bien penser qu'elles subissent une réflexion au centre et qu'elles rebroussent chemin, comme le montre l'animation suivante :

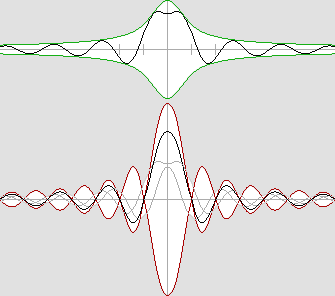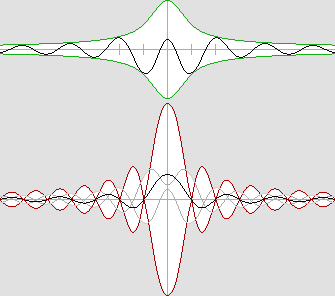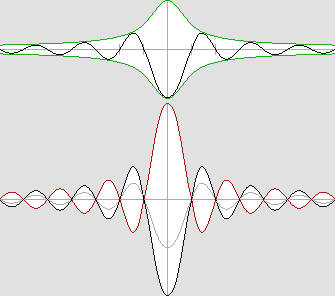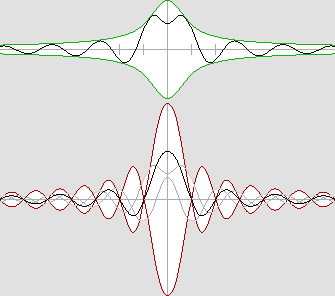
Une meilleure interprétation : les ondes sont réfléchies au centre du noyau.

M. Jocelyn Marcotte a observé qu'il s'agissait d'une réflexion dite "dure".

Ce qui se passe vraiment, d'un point de vue mécanique, c'est que les ondes stationnaires théoriquement parfaites rebondissent sans fin les unes sur les autres. Alors il n'y a pas de transport d'énergie. Toutefois l'électron ne se comporte pas ainsi parce qu'il est amplifié ; l'énergie acquise doit ensuite être rayonnée, et c'est pourquoi l'amplitude de ses ondes divergentes est supérieure à celle de ses ondes convergentes, surtout si la distance du centre devient importante.

On peut aussi considérer que l'électron absorbe de l'énergie et qu'il la véhicule ensuite vers l'extérieur à travers ses ondes stationnaires.

Des applications étonnantes.

Les ondes stationnaires sphériques seront certainement exploitées dans le futur, car elles présentent des propriétés uniques. Je citerai ici deux exemples, que j'ai mentionnés sur mon blog les 15 et 21 février 2007.

La centrale à « fusion nucléaire acoustique ».

La pression très élevée à l'intérieur du noyau central peut être utilisée pour confiner le processus de fusion nucléaire à l'intérieur d'un espace restreint libre de toute matière solide.

En fait, il faut à la fois une pression et une température considérables pour que la fusion de l'hydrogène en hélium s'opère spontanément. C'est ainsi que la Russie a réussi à expérimenter en 1961 une bombe de 57 mégatonnes (57 millions de tonnes de TNT !) en ayant recours à une bombe au plutonium en guise de détonateur.

Le projet international ITER, basé à Cadarache, y arrivera sans doute par des moyens magnétiques, mais au prix d'un matériel extrêmement complexe et coûteux. On sait que la fusion nucléaire s'opère spontanément à l'intérieur du Soleil, et qu'on y a détecté depuis longtemps des champs magnétiques formidables. Mon modèle de l'atome d'hydrogène indique qu'il s'agit véritablement d'un aimant minuscule qui a besoin d'un autre atome d'hydrogène contenant un électron et un proton de spin opposé pour produire aussi bien une molécule d'hydrogène qu'un atome d'hélium. Selon le spin des électrons et des protons, il peut exister quatre sortes d'atomes d'hydrogène, et l'expérience de Stern et Gerlach montre qu'on ne peut les séparer qu'en deux groupes. Cela constitue tout de même un progrès, puisque l'atome d'hélium contient forcément les quatre spins à lui seul dans ses deux électrons et ses deux protons. Les champs magnétiques ont ainsi pour effet de faciliter la fusion en plus de la contenir dans un espace restreint.

Selon moi, des ondes stationnaires sphériques produites à l'intérieur d'une très grande sphère fortement chauffée et pressurisée suffiraient à réaliser la fusion nucléaire. Mais puisque l'un n'empêche pas l'autre, le fait de produire des ondes stationnaires concentriques à l'intérieur du dispositif mis au point à Cadarache ne pourrait que faciliter le processus.

De plus, on a inauguré en 2009, en Californie, USA, un laser à faisceaux multiples capable de réaliser la fusion nucléaire uniquement par ce moyen. Là encore, j'affirme qu'on pourrait améliorer le processus à l'aide d'ondes stationnaires sphériques. On pourrait même superposer aux lasers un grand nombre de magnétrons synchronisés dirigeant leur faisceau au même endroit de manière à produire encore plus de chaleur grâce aux micro-ondes. Il se peut même que les champs magnétiques ainsi produits permettent d'améliorer encore les résultats.

La formule magique.

Ceux qui prendront la peine d'étudier un peu plus attentivement la formule de l'électron que M. Jocelyn Marcotte a donnée comprendront vite que la pression d'un gaz enfermé dans une sphère gigantesque peut atteindre des valeurs énormes si la longueur d'onde est relativement courte. Comme on l'a vu plus haut, cette formule se lit comme suit :

y = sin(x) / x

avec x = 2 * pi * distance / lambda

Le noyau des ondes stationnaires sphériques peut produire un pression considérable.

La cinquième calotte sphérique (en vert) se situe à cinq longueur d'ondes et quart du centre.

La pression au centre est : 5 * 2 * pi + (pi / 2) = 33 fois plus forte que dans cette calotte, soit: 1 / (sin 33 radians / 33).

Mais elle serait 66 fois plus forte pour une même distance si on doublait la fréquence.

La variable x valant : 2 * pi * distance / lambda, on voit bien que la longueur d'onde est déterminante. Au centre, malgré la division de zéro par zéro, on a en réalité la pression de référence : y = 1. À partir de la pression requise pour que la fusion nucléaire s'opère, on peut facilement calculer la pression des ondelettes de Huygens sonores qu'il faut générer à la périphérie d'une sphère.

Le moteur à piston acoustique.

Ce moteur n'est peut-être pas véritablement une invention, car je suppose que quelqu'un, quelque part, a déjà songé à un tel dispositif. En fait, mon but est de montrer une fois de plus que les ondes stationnaires sphériques présentent des propriétés étonnantes. En particulier, la pression du gaz à l'emplacement des nœuds de pression ne varie jamais ; c'est pourquoi la présence de soupapes y devient inutile pourvu que les ondes soient suffisamment stationnaires. De plus, puisque la pression à l'échappement est constante, le moteur est remarquablement silencieux malgré l'absence de pot d'échappement.

Le vert représente une pression inférieure à la pression atmosphérique.

Le rouge et en particulier le rouge clair indique que la pression sur le piston est plus forte.

Ce moteur doit tourner en régime constant, ce qui est un inconvénient majeur. Il serait néanmoins possible de l'utiliser dans une centrale électrique au gaz naturel, par exemple. Un moteur dont le régime serait de 60 Hz n'aurait pas besoin de roue à erre car une simple bobine d'induction faisant l'aller et retour dans un champ magnétique suffirait pour produire un courant de 60 Hz. Cette fréquence suppose une longueur d'onde de 5,6 m à la pression atmosphérique, d'où une chambre à combustion conique relativement grande faisant aussi 5,6 mètres. La pression au troisième ventre de pression situé sur la surface sphérique est de 2 * pi = 6 fois plus faible que celle qui s'exerce sur le piston.

La forme conique a un effet multiplicateur important, comme c'est le cas pour la centrale nucléaire proposée plus haut. Il est possible de varier l'angle du cône de manière à ajuster la compression sans avoir recours aux mélanges anti-détonants des moteurs à haute compression : ainsi la pression réelle sur le piston est ajustable et différente de celle où a lieu l'explosion. Même si la cylindrée se limite en principe au volume du ventre situé côté piston, d'autres ventres peuvent participer à la combustion tout en achevant celle du cycle précédent. Des bougies d'allumage peuvent être installées à chacun des ventres de pression, mais elles ne sont pas nécessaires dans la mesure où l'explosion peut s'effectuer spontanément par compression et par chaleur comme dans un diesel. Ce système offre donc plus de latitude pour réduire les émissions nuisibles, ce qui signifie qu'il n'aurait pas besoin non plus de convertisseur catalytique.

Puisque le piston bouge, la réflexion dure est remplacée par une réflexion molle. Il peut exister un espace étanche (facultatif) à l'arrière du piston, mais dont les dimensions devraient être très faibles. Ceux qui connaissent le fonctionnement des haut-parleurs de type "bass reflex" comprendront que le poids du piston et de son entraînement doit s'ajouter au poids de l'air dans l'espace vide de manière à obtenir une résonance maximum à 60 Hz dans le cas présent, compte tenu des pulsations qui s'exercent de l'autre côté.

Voici aussi un modèle de fusée tout à fait original :

Veuillez noter que la pression moyenne est affichée en noir ; le vert représente le vide.

Les ondes stationnaires à l'intérieur du cône produisent de fortes pulsations à la sortie.

Les gaz ne sont expulsés que pendant la moitié d'un cycle, mais à une vitesse supérieure. Pour une quantité donnée d'oxygène et de carburant, la poussée est donc supérieure, du moins en principe. Il est clair que ce modèle serait extrêmement bruyant et que la chambre à combustion détruit l'aérodynamisme de la fusée, de telle sorte qu'elle ne serait utile que dans l'espace. J'ai aussi songé à une turbine acoustique, les pulsations montrées ci-dessus agissant comme des engrenages sur ses ailettes. Ces dispositifs sont intéressants du point de vue de la physique, mais peut-être aussi peu avantageux que le moteur montré plus haut d'un point de vue pratique. Ça reste à vérifier.

Je crois fermement que les ondes stationnaires sphériques permettront un jour de réaliser des dispositifs fabuleux.

J'y travaille !

Les transformations de Lorenz.

Pour terminer, il faut souligner que, dans le cas de l'électron mobile, qui subit l'effet Doppler, on assiste en plus à une réduction de la fréquence, qu'on a interprétée à tort comme un ralentissement du temps. Il faut donc tenir compte d'une dilatation de la longueur d'onde de référence quand vient le temps de déterminer l'effet Doppler selon la direction des ondes.

Il s'agit en pratique de satisfaire aux équations complémentaires des transformations de Lorentz : y' = y ; z' = z. Si la fréquence demeurait stable, il se produirait une contraction de la longueur d'onde dans les directions orthogonales selon l'inverse du facteur gamma. L'allongement de la longueur d'onde de référence selon le facteur gamma a pour conséquence de neutraliser cette contraction dans les directions orthogonales.

C'est en effet l'une des conclusions les plus étonnantes de cette étude : les transformations de Lorentz ne concernent rien d'autre et rien de plus que l'effet Doppler très particulier que subissent les ondes stationnaires sphériques de l'électron, comme le montre incontestablement le programme Ether17.exe Ether17.bas.

La Relativité.

On a eu tort d'attribuer aux transformations de Lorentz des propriétés tout à fait hallucinantes et délirantes telles que la transformation de l'espace et du temps. On peut beaucoup plus facilement et raisonnablement invoquer une transformation de la longueur d'onde et de la période des ondes stationnaires de l'électron. Il est clair que si l'électron assemble les molécules selon un multiple d'une longueur d'onde bien définie, les proportions de la matière qui en résulte en sont affectées.

Il est tout aussi clair que si la fréquence de l'électron diminue, c'est toute la vitesse d'évolution de la matière qui ralentit. Par exemple, à grande vitesse, le temps de vie d'un muon ou d'un isotope radioactif en sera prolongé, et les horloges indiqueront des heures plus lentes. Bien évidemment, des horloges qui ralentissent n'ont pas le pouvoir de "dilater le temps" !

Alors on comprend que les transformations de Lorentz sont absolues. L'éther constitue non seulement un référentiel privilégié, mais c'est aussi le seul référentiel acceptable. Les transformations de Galilée étant inexactes, il ne peut exister de référentiels galiléens. Tout est là : l'unique référentiel que constitue l'éther est cartésien, et ses coordonnées sont absolues. Bien sûr, nous ne saurons peut-être jamais comment le repérer, mais ce n'est pas bien grave. Il suffit de considérer qu'il existe. On sait qu'Henri Poincaré a hélas ! mis l'existence de l'éther en doute, mais il a aussi écrit, avec beaucoup d'à propos :

« ...l'essentiel pour nous c'est que tout se passe comme s'il existait et que cette hypothèse est commode pour l'explication des phénomènes. »

La Relativité d'Albert Einstein, publiée en 1905, est désespérément illogique et dogmatique.

Au contraire, la Relativité que Lorentz a découverte vers 1904 et même avant est remarquablement cohérente. Depuis peu, elle présente un autre avantage, et il est immense : on peut désormais l'expliquer, grâce aux propriétés étonnantes des ondes stationnaires sphériques.

| 01 | 02 | 03 | Vous êtes ici. | 05 | 06 | 07 | 08 | 09 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |

| 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 |

Gabriel LaFrenière,

Bois-des-Filion en Québec.

Sur l'Internet depuis septembre 2002.

Dernière mise à jour le 17 décembre 2009.

Courrier électronique : veuillez consulter cet avis.