LE SCANNER DU TEMPS

|
|
|
Le Scanner du Temps provoque un effet Doppler s'il traite des ondes normales.
Inversement, il peut aussi annuler l'effet Doppler, selon l'intention initiale de Woldemar Voigt en 1887.
Ce dispositif reproduit donc les transformations de Lorentz, car ce n'est rien d'autre qu'un calcul de l'effet Doppler.
Il en résulte une contraction des distances, un ralentissement des horloges et un décalage horaire.
Cela permet d'expliquer la Relativité.
Voici des vidéos qui montrent ce phénomène avec plus de précision :
Vous pouvez aussi examiner les programmes FreeBASIC qui ont produit ces images :
![]()
![]() Page
d'accueil : La matière
est faite d'ondes.
Page
d'accueil : La matière
est faite d'ondes.
|
J'ai inventé en mars 2004 un procédé qui permet de reproduire les transformations de Lorentz. Il s'agit d'un scanner qui balaie un espace contenant des objets, et qui en produit une image d'autant plus contractée que leur vitesse approche celle de la lumière. On comprendra qu'un scanner produit d'une scène animée une image où les événements n'ont pas eu lieu au même instant. J'ai donc eu l'idée de faire coïncider ce temps local avec celui qui a été découvert par Lorentz et c'est pourquoi j'ai appelé ce dispositif "le Scanner du Temps". L'animation ci-dessus montre clairement que si les objets sont des émetteurs d'ondes, on obtient un effet Doppler. Pourtant, le même dispositif peut au contraire corriger l'effet Doppler, selon la vitesse de déplacement de l'émetteur ou le sens du balayage. On retrouve la même réciprocité dans les équations des transformations de Lorentz telles que présentées par Henri Poincaré en 1904. Cette animation montre aussi que si les objets sont des horloges, celles-ci affichent sur l'image finale des heures différentes selon l'emplacement qu'elles occupent sur l'axe du déplacement. Il s'agit du célèbre "temps local" découvert par Lorentz lui-même. De plus, si ce dispositif produit de nombreuses images successives, et si on affiche celles-ci en succession comme les images d'un film, ces horloges indiquent des heures plus lentes. Grâce à l'échelle verticale, on peut vérifier que la longueur d'onde demeure constante sur les axes orthogonaux. On a donc, comme le prévoyait Lorentz: y' = y; z' = z. Il faut savoir que l'effet Doppler normal provoque une contraction de la longueur d'onde sur ces axes. Cette longueur d'onde constante ne peut s'expliquer que si la fréquence d'un émetteur en mouvement ralentit selon les prévisions de Lorentz. Et enfin, si le scanner balaye de nombreux objets dont la vitesse et la direction n'est pas la même, il produira de ces objets une image telle qu'elle apparaîtrait dans un référentiel dont la vitesse est différente. Ainsi, le Scanner du Temps est bien plus polyvalent, bien plus versatile que les équations de Lorentz. Il est capable de réaliser un nombre illimité de transformations en une seule opération et sur la totalité des coordonnées au lieu d'une seule à la fois. Il peut même réaliser des images en trois dimensions, le scanner balayant alors la scène sur toute la surface d'un plan mobile. Il s'agit donc d'un outil indispensable pour étudier la mécanique du mouvement, l'optique du mouvement, les transformations de Lorentz et la Relativité. Un observateur en mouvement se méprend sur ce qu'il voit. On comprendra facilement qu'à cause de l'effet Doppler, à distance égale, les événements qu'un observateur en mouvement voit se sont déroulés plus tard à l'avant qu'à l'arrière. Le temps local de Lorentz n'existe pas vraiment, il est simplement le résultat d'une méprise. En corrigeant cette distorsion, le Scanner du Temps permet de montrer très facilement ce qui se passe en réalité. Inversement, en introduisant cette distorsion, il peut tout aussi bien montrer ce qu'un observateur en mouvement voit d'un système parfaitement au repos. Les équations réversibles de Poincaré sur les transformations de Lorentz avaient le même but. Le Scanner du Temps est éminemment utile car il n'existe pas d'autre manière de montrer comment un observateur en mouvement perçoit un phénomène optique dans son environnement. Étrangement, celui-ci perçoit un effet Doppler dans les ondes d'un système au repos, même si cet effet Doppler n'existe pas. Mais il n'en perçoit pas dans les ondes qui sont émises dans son propre environnement, et qui pourtant sont bel et bien affectées par l'effet Doppler. Et puisque la matière est faite d'ondes, ce qu'un observateur en mouvement perçoit de la matière au repos suit les mêmes règles. Les transformations de Lorentz. Hendrik Antoon Lorentz a découvert que la matière doit se transformer à grande vitesse : 1 – Elle se contracte sur l'axe du déplacement. 2 – Elle évolue plus lentement, les horloges affichant alors des heures plus lentes. 3 – Ces horloges présentent aussi un décalage horaire, celles situées à l'avant affichant un retard. Un bref rappel s'impose. On aura vu à la page précédente que Lorentz a présenté ses équations en précisant qu'il ne s'agissait que d'un artifice mathématique. Leur fonction était de modifier les équations de Maxwell de manière à ce qu'elles annulent l'effet Doppler et les rendent invariantes peu importe la vitesse d'un système de référence. Mais Lorentz avait expliqué que l'interféromètre de Michelson devait se contracter de manière à annuler la différence de vitesse de la lumière sur deux trajets orthogonaux. D'ailleurs, même la théorie de la Relativité d'Albert Einstein parle d'une contraction et d'un "ralentissement du temps". Bref, lorsque le temps t est à zéro, la valeur de la variable x' doit être inférieure, et non pas supérieure à celle de x. Il faut en effet convenir que les variables x et t devraient logiquement s'appliquer au référentiel au repos. Pour que les équations de Lorentz produisent réellement cet effet, j'ai donc dû les inverser comme ceci:
Les transformations de Lorentz inversées, à gauche. Si l'on extrait x, on retrouve la forme originale de Lorentz: x = (x' – bêta * t) / g Il faut toutefois permuter x et x' pour obtenir l'équation proposée par Lorentz: x' = (x – bêta * t) / g Les équations symétriques inversées montrées à droite correspondent plutôt à celles de Henri Poincaré.
Ces équations inversées sont bien plus limpides que celles données par Lorentz. En omettant la translation qui correspond à bêta * t et le décalage horaire qui est donné par –bêta * x, la matière se contracte selon g * x et les heures ralentissent selon g * t. Ça ne pourrait pas être plus clair. Dans le cadre d'une Relativité mal comprise, le facteur gamma prêtait à confusion et il vaut donc mieux l'éviter la plupart du temps. Son utilisation en mécanique ondulatoire demeure valable puisque ces phénomènes vont bien au delà de la Relativité. En général, il faudra lui préférer le facteur de contraction de Lorentz puisqu'il est effectivement question d'une contraction et d'un ralentissement: x' = g * x + bêta * t t' = g * t – bêta * x
Les effets des transformations de Lorentz sont absolus. Voilà donc la version véritable des transformations de Lorentz, celle qui correspond à la pensée de Lorentz, et qu'il était essentiel de bien saisir avant d'aborder le Scanner du Temps. Rappelons que l'idée d'une transformation de l'espace et du temps est ridicule. Tout cela se produit uniquement parce que la fréquence des électrons ralentit. À cause de l'effet Doppler, cela entraîne malgré tout une contraction de ses ondes stationnaires uniquement sur l'axe du déplacement, et donc une contraction de la matière dont la structure dépend des électrons. Même les espaces vides d'une structure matérielle se contractent parce que les ondes stationnaires des champs de force qui en assurent les propriétés mécaniques se contractent. Bien évidemment, les horloges n'ont pas le pouvoir de transformer le temps. C'est plutôt la mécanique de la matière en mouvement qui ralentit en fonction de la fréquence de l'électron. Les horloges en mouvement ne font qu'afficher des heures plus lentes qui sont tout simplement inexactes comparativement à l'heure absolue décrétée par convention, quelle qu'elle soit. Ce n'est que très récemment que nous avons pu convenir que la longueur du mètre devait correspondre à un multiple d'une certaine longueur d'onde, et que le temps pouvait être établi selon une certaine fréquence, le tout par convention de manière à exclure toute transformation ultérieure de ces valeurs. Peu importe notre vitesse réelle à travers l'éther, elles deviennent alors absolues. Dans ce contexte, il convient de préciser que les variables x et x' des transformations de Lorentz ne s'appliquent pas à l'espace mais bien à une certaine longueur d'onde, celle de l'électron; les variables t et t' ne s'appliquent pas au temps, mais bien à une certaine fréquence, celle de l'électron. Or ces grandeurs varient selon la vitesse d'un système ondulatoire à travers l'éther à cause de l'effet Doppler. De plus, la théorie de la Relativité d'Albert Einstein ne pouvait traiter que deux référentiels à la fois, et elle aboutissait de toutes façons à des paradoxes, qui avouons-le n'étaient que des contradictions. Le Scanner du Temps ne présente pas cet inconvénient. Il permet de traiter simultanément des dizaines de référentiels, comme si on les accélérait ou les ralentissait dans leur ensemble. Mais surtout, l'animation qui figure au début de cette page montre de manière spectaculaire qu'il existe toujours un référentiel privilégié où la contraction n'intervient pas. En effet, à la condition d'avoir recours à un référentiel dont la vitesse est intermédiaire (voir "la vitesse de déplacement alpha" plus bas), le texte et les graphiques stationnaires ne sont aucunement modifiés. Il est donc faux de prétendre que l'espace doive obligatoirement se transformer car ce n'est pas nécessairement le cas. |
![]()
CALCUL ET PROCÉDURE
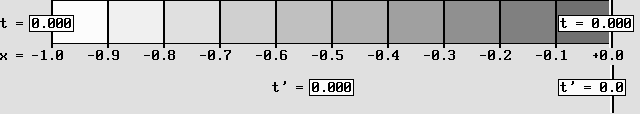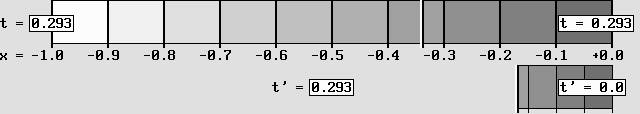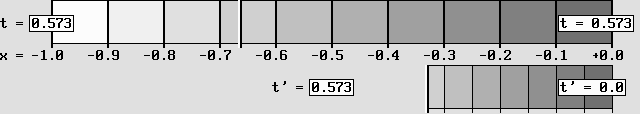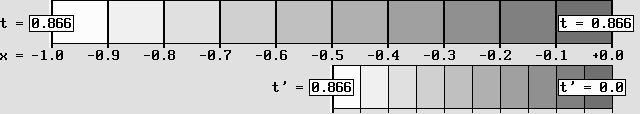
Ici, on obtient une contraction parce que la vitesse d'impression est plus lente que la vitesse de balayage.
Cette méthode alternative reproduit tout aussi bien les transformations de Lorentz.
La contraction atteint 50%, soit selon le facteur de contraction de Lorentz: g = 0,5 avec bêta = 0,866.
Le décalage horaire équivaut à – bêta, soit 0,866 secondes lentes de retard à l'horloge située à l'avant (à droite).
|
On peut obtenir une contraction en déplaçant peu à peu le référentiel à transformer à la "vitesse alpha" (voir plus bas), et alors la vitesse de balayage est la même que la vitesse d'impression. Mais l'animation ci-dessus a plutôt recours à une vitesse d'impression plus lente que la vitesse de balayage. Dans ce cas, il ne faut pas déplacer le référentiel. Le diagramme animé montré ci-dessus est conforme aux transformations de Lorentz. Le point situé en x = –1 seconde-lumière se contracte vis-à vis la coordonnée x' = –0,5 en mesures absolues selon le facteur de contraction g. Peu importe le temps t écoulé, l'horloge située à l'avant retarde toujours sur celle qui est à l'arrière. Ce "temps local" correspond à une décalage horaire égal à –bêta, donc ici –0,866 seconde lente pour chaque seconde-lumière d'écart avant contraction. Il faut garder à l'esprit que les horloges en mouvement indiquent des secondes plus lentes en plus de présenter un temps local. La vitesse de balayage correspond à celle de l'onde de phase. Le
principe du Scanner du Temps est vraiment très simple puisqu'il table
sur la vitesse de "l'onde de phase" dont parle Louis de
Broglie et qu'il a établie à: V = c ^ 2 / v. Cette vitesse vaut plus
simplement 1 / bêta si elle se mesure
en secondes-lumière par seconde ou encore en longueurs d'onde par
période d'onde. Pour ceux qui ne l'auraient
pas encore observée, cette onde de phase est très visible dans la
partie de droite de l'animation
montrée ci-dessous. Elle se manifeste par des
bandes verticales sombres régulièrement espacées qui défilent vers
la droite.
L'onde de phase est très visible dans mon électron
mobile. Vous pouvez aussi examiner la séquence suivante, qui montre d'abord des ondes planes, puis des ondes courbées qui entrent in interférence. Le curseur mobile suit l'onde de phase qui en résulte: Le programme : Phase_Wave.bas Phase_Wave.exe Voilà donc l'effet le plus évident d'un scanner : si la scène est animée, il produit d'elle une image sur laquelle les événements ne se sont pas produits au même instant. Le Scanner du Temps balaie véritablement le temps. Dans l'animation montrée an début de cette page, on observe qu'il transforme des ondes concentriques de manière à ce qu'elles semblent subir l'effet Doppler. Mais on observe aussi que la règle graduée mobile de même que les deux horloges subissent une contraction tout en indiquant finalement un "temps local", le tout conformément aux prévisions de Lorentz. Ceux qui prendront la peine de bien mesurer la longueur d'onde avant et arrière sur cette animation constateront que ces ondes n'ont pas subi l'effet Doppler normal, qui ont le sait s'effectue selon 1 + bêta et 1 – bêta. On a plutôt (1 + bêta) / g et (1 – bêta) / g. C'est que la fréquence de l'émetteur ralentit selon le facteur g. Je répète ici que pour la même raison, la longueur d'onde est demeurée inchangée sur l'axe transversal selon les prévisions de Lorentz: y' = y; z' = z. Sachant que l'effet Doppler normal comprime la longueur d'onde selon le facteur g sur un plan orthogonal, on a ici un indice que les événements dans un tel système se déroulent plus lentement selon le facteur g. La vitesse de balayage. En procédant par tâtonnements, on se rend compte qu'il n'existe qu'une seule vitesse de balayage capable de reproduire l'effet Doppler caractéristique d'une vitesse d'entraînement donnée. Que la fréquence ralentisse ou non, on sait que le rapport de longueur R entre les ondes comprimées et dilatées vaut toujours : R = (1 + bêta) / (1 – bêta) Selon notre exemple (bêta = 0,866 et g = 0,5), ce rapport vaut : R = 13,928. La vitesse de balayage sera notée ici par la majuscule V. Il s'agit d'une vitesse normalisée et elle se mesure donc en secondes-lumières par seconde ou encore en longueurs d'onde par période. Au début du balayage, le scanner va au devant des ondes, dont la vitesse est celle de la lumière : c = 1 selon Poincaré. Leur vitesse relative vaut donc: V + 1. Mais dès qu'il a dépassé l'émetteur d'ondes, cette vitesse relative vaut V – 1. Il s'agit bien sûr de reproduire le même rapport R indiqué ci-dessus, et donc de respecter l'équation: (V + 1) / (V – 1) = (1 + bêta) / (1 – bêta) En simplifiant : V = 1 / bêta = 1,1547 On trouve par ce moyen que dans notre exemple, la vitesse de balayage doit être égale 1,1547 seconde-lumière par seconde (ou longueurs d'onde par période). Le but de cet exercice est de montrer qu'on peut retrouver sans peine les grandeurs des transformations de Lorentz grâce au Scanner du Temps, donc par un chemin différent de celui suivi par Lorentz, Larmor ou Poincaré. On verra plus loin que la vitesse de balayage peut être la même que la vitesse d'impression, soit g / bêta, à la condition de déplacer tout le référentiel qu'on veut transformer à la vitesse moyenne intermédiaire "alpha" donnée par (1 – g) / bêta de manière à compenser ce déplacement. La vitesse d'impression. Si le référentiel n'est pas déplacé, la vitesse d'impression "Vi" doit être plus lente que la vitesse de balayage afin d'obtenir une contraction selon le facteur g. Vi = g / bêta Vi = 0,577 seconde-lumière par seconde (ou longueur d'onde par période). Il s'agit en pratique de repérer la vitesse d'impression qui produit des ondes sphériques, ce qui conduit tout droit au facteur de contraction g sans même l'aide de Lorentz. Il faut se rappeler l'une des propriétés remarquables des ondes stationnaires, à savoir leur contraction. On aura vu que ces ondes, si la fréquence d'émission demeure inchangée, donc selon Michelson, se contractent même sur un axe transversal y ou z selon le facteur de contraction g de Lorentz. Leur contraction est encore plus sévère sur l'axe du déplacement, soit selon le carré de ce facteur:
La contraction selon Michelson est trop sévère. Pour l'éviter, il faut ralentir la fréquence des ondes stationnaires. On a ici bêta = 0,866 et g = 0,5 selon notre exemple.
Cette contraction trop sévère correspond aux calculs de Michelson, faits avant 1887. Il est donc probable que Woldemar Voigt se soit inspiré de ces calculs pour présenter ses propres transformations cette année-là, et qu'il appliquait aux équations de Maxwell dans le but de compenser l'effet Doppler. Or non seulement ces équations étaient imprécises à cause de la présence d'une constante indéterminée, mais elles étaient franchement erronées. Je présente ci-dessous la version corrigée, et dans laquelle les variables x et x' sont inversées. La valeur de la constante de Voigt k doit être égale au facteur g s'il faut reproduire l'effet Doppler normal (donc sans ralentissement de la fréquence) prévu par Michelson:
Les transformations de Voigt revues et corrigées. Si k est égal à g, l'effet Doppler est normal car il n'y a pas de ralentissement de la fréquence. On a tout simplement: t' = t avec x = 0
Les transformations de Lorentz inversées. On voit bien qu'il s'agit à toutes fins pratiques des équations de Voigt, la constante en moins. Les équations symétriques montrées à droite sont celles de Henri Poincaré, mais dans leur forme inversée.
Selon Lorentz, la fréquence du système ondulatoire montré en début de page doit ralentir de manière à allonger la longueur d'onde. Il savait sûrement que l'effet Doppler normal comprime les ondes transversales selon le facteur g. C'est pourquoi le ralentissement de la fréquence provoque une dilatation de la longueur d'onde qui annule cette contraction. Au début, Woldemar Voigt avait indiqué une correction sur les axes y et z, selon une constante indéterminée. Lorentz avait montré dès 1895 qu'il aurait pu s'agir aussi bien d'une contraction que d'une dilatation indéterminées; dans tous les cas, l'interféromètre de Michelson aurait présenté un résultat nul. Il semble que Joseph Larmor fut le premier à proposer l'invariance transversale dès 1897 mais les chiffres qu'on cite dans les comptes rendus ne correspondent pas à cette solution. Pour autant que je sache, c'est Lorentz qui a proposé le premier les formules correctes. Il l'a fait avant 1901 puisque Poincaré les mentionne cette année-là et les approuve en invoquant le principe de moindre action qui se vérifie si la constante de Voigt est égale à 1. Mais Lorentz ne les a publiées qu'en 1904. Le Scanner du Temps confirme que Lorentz et Poincaré avaient raison d'éliminer cette constante, qui n'est plus utile puisqu'elle doit être égale à 1. Finalement, il ne se produit pas de contraction des ondes sur les axes orthogonaux : y ' = y z ' = z Tout bon programmeur sait bien que la moindre erreur dans un programme produit le plus souvent des résultats anormaux très perceptibles, souvent même catastrophiques. L'avantage d'un ordinateur, c'est qu'il vérifie les équations. Si celles-ci sont erronées, le programmeur en est généralement informé brutalement. Or l'ordinateur montre que les équations de Voigt et de Lorentz telles qu'indiquées plus haut dans leur forme inversée sont correctes. Elles ne fonctionnent pas dans leur forme originale, qui implique une "transformation de l'espace-temps" tout à fait inutile, arbitraire et irréalisable que l'ordinateur refuse (fort heureusement!) de montrer. Doppler_Voigt_transformations.bas Doppler_Voigt_transformations.exe On pourrait aussi invoquer le principe de moindre action comme l'a fait Henri Poincaré. Ce dernier mentionne que Lorentz est parvenu à déterminer que la constante de Voigt (notée par la lettre l dans le texte) devait être égale à 1 en procédant "par tâtonnements". Cela ressemblait assez à un reproche. Le simple fait d'attribuer à la constante de Voigt une grandeur différente de 1 introduit effectivement une "action" supplémentaire qui se traduit par des effets anormaux qui deviennent vite très perceptibles et qui font en sorte que la Relativité ne peut plus se justifier. On peut dire qu'au lieu de démontrer pourquoi la Relativité est vraie, Poincaré a pris pour acquis qu'elle était vraie, quitte à attendre que les preuves s'accumulent ensuite. Même s'il a vu juste à propos de l'absence de contraction transversale, ce n'était pas un argument très convaincant. Personnellement, en tant que chercheur, j'évite les principes le plus possible surtout lorsqu'ils s'appliquent à n'importe quoi sans règles bien définies. J'ai toujours préféré suivre un fil d'Ariane, plus exactement une extrapolation faite à partir de quelques observations plus ou moins précises. Il en va des principes comme des balises. Avant de les poser, il faut d'abord connaître l'emplacement de l'écueil, du précipice, etc. Les balises et donc les principes ne seront utiles qu'à ceux qui suivent, et encore faut-il qu'ils soient correctement posés! Si donc une vérité nous échappe, il est rare qu'un principe puisse nous la faire découvrir. Dans ce contexte, le Scanner du Temps est bien plus efficace et versatile que les équations de Lorentz. Il montre beaucoup mieux comment les ondes et même la matière réagissent au mouvement, et le résultat confirme la Relativité. Or cela implique une contraction des objets, qui s'avère obligatoire. En particulier, j'ai pu démontrer grâce au médium virtuel Delmotte-Marcotte que la parabole d'un émetteur en mouvement doit se contracter pour continuer de produire des ondes planes. En voici un exemple: Bradley_Aberration_Plain.5c.mkv La contraction de la matière ne peut plus être considérée comme une simple hypothèse plus ou moins farfelue. Il s'agit là d'un fait réel dont il faut prendre acte. Ceux qui prendront la peine de le vérifier confirmeront que ceux qui ont rejeté cette idée, à commencer par Poincaré et Einstein, ont commis une erreur grave. Le Scanner du Temps et le médium virtuel Delmotte-Marcotte sont deux outils puissants qui faisaient cruellement défaut à l'époque. Désormais, ils apportent des preuves bien plus solides que Lorentz a vu juste. La vitesse de déplacement "alpha". La contraction
peut avantageusement être obtenue en déplaçant tout le
référentiel qu'on désire transformer à la
vitesse du référentiel privilégié, qui est le propre de la
Relativité de Lorentz. Il s'agit de la vitesse intermédiaire,
qui se
situe entre zéro et la vitesse bêta à obtenir. J'ai choisi de
l'appeler "alpha" puisqu'elle est inférieure à bêta. L'échelle des
vitesses n'étant pas linéaire, alpha ne correspond pas à la moitié de
bêta. Pour la trouver, il faut plutôt recourir à la loi de l'addition des vitesses de Poincaré :
bêta'' = (bêta + bêta') / (1 + bêta * bêta') Cette formule peut être simplifiée puisqu'on considère que deux référentiels se déplacent en sens opposé et à la même vitesse alpha comparativement à l'éther. De son point de vue, l'observateur présent dans l'un de ces deux référentiels en mouvement se pense au repos et c'est plutôt l'autre référentiel qui semble se déplacer à la vitesse bêta. Les deux observateurs impliqués obtiennent ainsi des résultats contradictoires qui conduisent au paradoxe des jumeaux. Mais du point de vue d'un observateur au repos intermédiaire, leur vitesse et donc leur contraction est la même. Leurs mesures du temps sont également les mêmes. Sous les transformations de Lorenz (et donc encore mieux après un balayage par le Scanner du Temps), ces grandeurs ne sont aucunement modifiées et peuvent donc servir de référence absolue même si le référentiel concerné (et privilégié) alpha se déplace. Le Scanner du Temps transformera le référentiel qu'on déplace à la vitesse alpha (mais qui n'est pas transformé) tel qu'il apparaîtrait s'il se déplaçait à la vitesse bêta. Mais il ne transformera pas le référentiel qui ne bouge pas car sa vitesse présumée –alpha deviendra + alpha, ce qui n'implique aucun changement dans les longueurs ni dans la mesure de l'écoulement du temps. Toutefois, le décalage horaire s'en trouvera inversé. Pour obtenir la valeur de la vitesse intermédiaire alpha, la formule de Poincaré peut être simplifiée ainsi: bêta = (2 * alpha) / (1 + alpha ^ 2) bêta = 2 / (1 / alpha + alpha) alpha = (1 – racine(1 – bêta ^ 2)) / bêta En intégrant le facteur de contraction de Lorentz g : alpha = (1 – g) / bêta
Tous les autres référentiels doivent présenter un effet Doppler, une contraction et une heure locale qui conviennent à leur vitesse telle qu'elle est observée dans le référentiel alpha. Ce dernier doit donc être représenté comme s'il était au repos, même s'il se déplace sur l'image. Et enfin, pour compenser ce déplacement, il faut modifier la vitesse de balayage. D'une manière remarquable, et c'est éminemment pratique, la vitesse de balayage devient la même que la vitesse d'impression qu'on a déterminée plus haut: V = Vi = g / bêta secondes-lumière par seconde. On aura remarqué que l'animation qui figure au début de cette page a été réalisée de cette manière. En premier lieu, puisque l'échelle des abscisses ne bouge pas, elle ne se transforme pas et les mesures qu'elle indique deviennent absolues. De plus, les variables x et x' des transformations de Lorentz inversées (montrées plus haut) font référence à cette même échelle et donc à un même espace cartésien invariable, alors que les équations originales de Lorentz avaient pour effet de définir un deuxième espace transformé et inconciliable. Désormais, on peut donc passer d'un référentiel à l'autre en emportant avec soi une échelle des longueurs et une mesure du temps qui ne varient jamais. Et enfin, même si elle se situe sur l'axe du déplacement x, l'échelle des longueurs correspond à la longueur d'onde transversale, qui on l'a vu ne varie jamais. Elle aussi est absolue.
Un autre avantage intéressant de la "méthode alpha", c'est qu'on peut ajouter plus facilement du texte et des graphiques statiques aux images. Le balayage ne fait que les reproduire intégralement, ce qui évite de provoquer des artéfacts ennuyeux. Le référentiel privilégié et la fin des paradoxes. Cette méthode qui consiste à privilégier un référentiel qui se déplace à la vitesse moyenne intermédiaire alpha est à mon sens beaucoup plus intuitive. L'observateur qui s'y trouve peut concilier les résultats à la satisfaction de chacun. Au contraire, la Relativité d'Einstein conduisait à des résultats contradictoires, qu'on avait essayé de tempérer en les appelant des "paradoxes". C'était le cas en particulier du paradoxe du train et du tunnel. Le tunnel étant présumé au repos, un train en mouvement semble plus court aux yeux d'un observateur également au repos. C'est apparemment le contraire si c'est le tunnel qui semble se déplacer, l'observateur étant alors dans le train qui lui semble au repos. Mais si l'observateur se déplace à la vitesse moyenne alpha, le train et le tunnel semblent se déplacer en sens inverse, mais à la même vitesse. Ils ont donc selon lui la même longueur. Les secondes s'y écoulent à la même cadence. Il n'y a plus de contradiction, et c'est pourquoi les mesures de temps et d'espace du référentiel alpha peuvent avantageusement être proclamées par convention à la satisfaction de tous. D'une manière encore plus évidente, lorsque des électrons ou des protons qui se déplacent en sens contraire entrent en collision dans un grand accélérateur, le référentiel privilégié est celui de l'accélérateur, où se situent les observateurs. Personne ne songerait à se préoccuper des deux observateurs qui se déplaceraient en sens contraire à la vitesse de ces particules, et qui auraient de cette scène une vision totalement différente. Leur vitesse relative leur apparaîtrait inférieure à celle de la lumière, alors que l'observateur privilégié sait bien que cette vitesse relative atteint près du double de celle de la lumière. Pour la même raison, les astronomes ont intérêt à présumer que notre galaxie se situe au centre de l'univers et qu'elle est au repos, même si c'est sans doute inexact. Autrement, ils pourraient difficilement concevoir que la vitesse de deux galaxies très éloignées puisse approcher celle de la lumière dans deux directions opposées. Même si la loi de la Relativité indique que tout observateur peut se considérer au repos, il vaut quand même mieux privilégier l'observateur qui, parmi plusieurs autres, obtient les résultats les plus acceptables pour tous. À défaut de certitude, le consensus a ses avantages. La vitesse alpha et la Relativité Générale. La vitesse alpha constitue en fait une innovation majeure en ce qui concerne la mécanique de la matière en mouvement, qu'on nommera éventuellement la mécanique du mouvement. Elle sera à la base d'une nouvelle "Relativité selon Lorentz" encore plus complète qui remplacera certainement la Relativité Générale d'Albert Einstein en faisant disparaître toute allusion à une prétendue transformation de l'espace-temps. Le point important, c'est que cette vitesse est réelle, car elle correspond en particulier à celle des champs de force électrostatiques, qui se situent entre les électrons et qui se déplacent donc à la vitesse intermédiaire. Il faudra aussi chiffrer les effets temporels d'une accélération et de la gravité, qui sont équivalents selon Einstein. Ce n'est pas un problème puisque ces effets sont mesurables. Plutôt que de prétendre que la gravité courbe l'espace, il faudrait d'abord connaître ses effets. Ensuite, il faudra invoquer des raisons mécaniques plus acceptables qu'une courbure de l'espace. La vitesse alpha permet d'expliquer en particulier pourquoi les électrons en mouvement continuent de se comporter comme si leur charge était négative. Puisque leur fréquence ralentit, ils deviennent en effet périodiquement des positrons comparativement aux électrons au repos présents dans la matière. En réalité, puisque les champs de force se situent à mi-chemin et bougent à la vitesse alpha, on peut considérer que de leur point de vue la période des électrons qui les ont créés demeure la même. Ces électrons semblent vibrer à la même cadence puisqu'ils semblent s'éloigner ou se rapprocher à la même vitesse. En définitive, le mouvement d'un certain nombre d'électrons en présence de matière présumée au repos introduit une rotation de phase dans les ondes stationnaires intermédiaires, et l'ensemble des champs de force qui en résultent justifie très bien les phénomènes électromagnétiques, y compris la force de Lorentz. Puisque toutes les forces sont attribuables à des champs de force, le même raisonnement s'applique à toute la mécanique de la matière dans son ensemble. En mettant à notre disposition une vitesse de référence alpha qu'il était pratiquement impossible de repérer autrement, le Scanner du Temps a déjà fait ses preuves. Désormais, on peut montrer que les transformations de Lorentz n'affectent pas nécessairement les mesures du temps et de l'espace. Le paradoxe des jumeaux. Avant toutes choses, il faut réaliser que l'effet Doppler très particulier découvert par Lorentz nous empêche de connaître la vérité absolue. Il sera toujours impossible de déterminer à quelle vitesse nous nous déplaçons réellement à travers l'éther. Pour cette raison, la manière véritable dont les jumeaux impliqués dans ce célèbre paradoxe évoluent nous échappe. Mais en désespoir de cause, on peut toujours évaluer tout un éventail de scénarios dont l'un correspond sûrement à la vérité absolue. Bien évidemment, on postulera que l'éther existe et que la vitesse de la lumière fait référence à l'éther tout comme la vitesse normalisée bêta. Le calcul s'avère d'autant plus intéressant qu'on peut prévoir que les résultats seront les mêmes à coup sûr puisque le Scanner du Temps nous indique qu'ils sont invariables peu importe le scénario envisagé. Le Scanner peut en effet reproduire la situation d'un observateur donné telle qu'elle lui apparaîtrait s'il était au repos, à partir de n'importe quel autre scénario où il ne l'est pas. Les transformations de Lorenz font en sorte que ces scénarios sont équivalents. S'il existe un Principe d'Équivalence en Relativité, c'est bien celui-là et non pas celui d'Einstein. Son application est d'une simplicité enfantine: le déroulement d'un événement semble toujours s'effectuer de la même manière peu importe la vitesse absolue de cet observateur. Il suffit donc en pratique de bien analyser une seule des hypothèses, la plus simple de préférence, pour avoir une vue d'ensemble de toutes les autres. C'est ce qui justifie le recours à un référentiel privilégié et à une vitesse alpha intermédiaire. Cette méthode a l'avantage énorme de ne pas aboutir à un paradoxe, pour ne pas dire une contradiction. Dans le cas de ces jumeaux, voyons de quoi il retourne. Ce qui est consternant, c'est que personne depuis un siècle (y compris Lorentz lui-même) n'a pris la peine de faire ces calculs. Ils sont pourtant relativement simples même en tenant compte des transformations de Lorentz. Considérons deux jumeaux identiques voyageant dans des fusées spatiales munies d'horloges très précises. Le jumeau A demeure constamment au repos comparativement à l'éther. À cause de l'absence d'effet Doppler, sa situation est privilégiée et ce sont donc ses mesures de temps et d'espace qu'on adoptera. Dans le but de vérifier les effets temporels découverts par Lorentz, le jumeau B accélère à la moitié de la vitesse de la lumière avant de passer à proximité de A. Cette manœuvre lui évite d'avoir à changer de référentiel inertiel. A et B synchronisent leurs horloges à zéro seconde au moment précis où ils se croisent. Un peu plus tard, lorsque son horloge indique 1 seconde, le jumeau A émet un signal radio afin que B le reçoive au moment où il aura parcouru une seconde-lumière, soit 300000 km. Il faut souligner le fait que si un troisième jumeau C s'éloignait en sens inverse, le jumeau A l'observerait de la même manière qu'il observe B. Puisqu'il s'agit ici de démontrer que tous les scénarios sont équivalents, la situation de A, qui est intermédiaire, s'avère ainsi doublement privilégiée. Au moment précis où il reçoit ce signal, le jumeau B a pour instruction de transmettre vers A un message radio indiquant l'heure que son horloge indique. Puisqu'une distance d'une seconde-lumière sépare B de A, ce dernier s'attend de recevoir le message de B lorsque son horloge indiquera 2,5 secondes, soit la durée de l'aller et retour plus le délai initial. Le jumeau B a mis 2 secondes pour parvenir à cet endroit, mais son horloge indique des secondes plus lentes proportionnellement au facteur de contraction de Lorentz: g = racine(1 – bêta ^ 2) = 0,866. Si Lorentz dit vrai, A s'attend donc à ce que le message transmis par B indique: 2 * 0,866 = 1,732 seconde. Un nouveau Principe d'Équivalence. Ce qui est remarquable, c'est qu'on obtient les mêmes résultats en analysant trois autres scénarios apparemment identiques du point de vue du jumeau A. En effet, puisque c'est invérifiable, il peut en toute bonne foi se considérer au repos comparativement à l'éther peu importe sa vitesse réelle. Pourtant, dans les trois scénarios proposés ci-dessous, le jumeau A se déplace à la moitié de la vitesse de la lumière (bêta = 0,5; g = 0,866) et le signal qu'il émet subit l'effet Doppler. Ce sont ses mesures de temps et d'espace qu'on adopte et c'est lui qui transmet le premier signal radio, toujours au moment où son horloge indique 1 seconde. Mais puisque son horloge est plus lente d'un facteur g, il s'est écoulé en réalité 1,1547 seconde et il a parcouru à ce moment 0,57735 seconde-lumière. 1 – C'est plutôt le jumeau B qui est au repos comparativement à l'éther, mais il l'ignore. Il voit donc A s'éloigner à la moitié de la vitesse de la lumière et il attend son signal. Le jumeau A émet ce signal après 1,1547 seconde et B le reçoit 0,57735 secondes plus tard. Il s'est écoulé 1,1547 + 0,57735 = 1,732 seconde, que B a chronométré correctement puisqu'il est au repos dans l'éther. 2 – Le jumeau B se déplace sur le même axe que A, mais plus rapidement encore que lui. Sa vitesse correspond à bêta = 0,8 avec un facteur de 0,6 en raison de la loi de l'addition des vitesse de Poincaré. De cette manière, A et B pensent tous les deux que leur vitesse relative correspond à bêta = 0,5 avec un facteur de 0,866. Il faut souligner que le jumeau A se trouve dans le référentiel intermédiaire "alpha" privilégié. En effet, avec bêta = 0,8 et g = 0,6, on obtient: alpha = (1 – g) / bêta = 0,5. C'est ce qui justifie l'application d'un nouveau Principe d'Équivalence qui fait en sorte que le jumeau A est doublement autorisé à se considérer au repos comparativement à l'éther. De cette manière, il est en mesure de concilier le référentiel d'un troisième jumeau C véritablement au repos avec celui de B, qui se déplace pourtant à la vitesse fantastique de 0,8 c. Étonnamment, A ne voit aucune différence entre B et C. 3 – Le jumeau B se déplace sur un axe transversal y comparativement à l'axe du déplacement de A. Après un délai de 2,3094 seconde, la distance qui sépare A de B correspond vraiment à une seconde-lumière selon Lorentz (y' = y). Le jumeau A a parcouru 1,1547 seconde-lumière alors que B a parcouru selon Pythagore: racine(1,1547 ^ 2 + 1) = 1,5275 seconde-lumière. Sa vitesse absolue vaut donc: 1,5275 / 2,3094 = bêta = 0,661427 avec un facteur g de 0,75 exactement. Ce qui est remarquable ici, c'est que l'horloge de B retarde d'un facteur additionnel de 0,866 comparativement à celle de A, qui retarde déjà du même facteur (0,866 ^ 2 = 0,75). C'est pourquoi A et B observent que leur vitesse relative vaut 0,5 c. Là encore, si un troisième jumeau C s'éloignait dans le sens opposé à B, le jumeau A l'observerait de la même manière qu'il observe B, ce qui confirme encore une fois sa situation privilégiée. Ce calcul élémentaire le prouve: les jumeaux A et B ne peuvent distinguer le scénario initial où A est au repos des trois autres scénarios décrits ci-dessus. Tout semble se passer exactement de la même manière dans tous les cas. Il y a bel et bien équivalence. Lorentz et Poincaré parlaient d'une invariance en appliquant les transformations de Lorentz aux équations de Maxwell. Or on voit bien que ces transformations ne s'appliquent pas seulement à des ondes, elles s'appliquent également à la matière. Cela ne peut s'expliquer que si la matière elle-même est faite d'ondes.
Les effets d'un changement de référentiel inertiel. Selon Lorentz et Einstein, tant qu'il existe une différence de vitesse entre A et B, tous les deux devraient observer que l'autre subit une contraction selon le facteur g. Ils devraient aussi observer que l'horloge de l'autre indique des heures plus lentes selon le même facteur. Et enfin, ils devraient observer que l'autre est victime d'un décalage horaire selon: –bêta * x. Voilà bien le paradoxe: c'est toujours "l'autre" qui semble subir les transformations de Lorentz. Logiquement, c'est impossible. Il faut donc trouver une explication à ce prodige. Bien évidemment, c'est seulement au moment où B sera de retour auprès de A qu'on pourra vérifier hors de tout doute lequel des deux jumeaux aura le moins vieilli en comparant leurs horloges. Mais pour que leur réunion soit possible, B doit changer de référentiel inertiel. Cela pourrait avoir une influence additionnelle sur l'heure que son horloge indique pour des raisons que Lorentz n'a pas prévues. On pense en particulier à un "effet d'ascenseur", qui est très perceptible au moment d'une accélération ou d'une décélération, et qui pourrait équivaloir à l'effet que produit la gravité selon le Principe d'Équivalence d'Einstein. Toutefois, si un tel effet existe, il n'est pas pertinent d'en tenir compte ici puisqu'il est invariable peu importe la distance parcourue. Si celle-ci est considérable, l'effet d'ascenseur devient négligeable toutes proportions gardées. De toutes façons, il est mesurable; un jour, on le mesurera et alors ceux qui s'accrochent à la théorie d'Einstein devront faire face à leurs erreurs. Selon Lorentz, c'est très clairement B, c'est à dire le jumeau qui change de référentiel inertiel (dans le but de revenir vers A) qui vieillit le plus lentement. La raison est très simple: quel que soit le scénario, il parcourt une plus grande distance. Pourtant, pendant toute la durée de l'expérience, ces deux jumeaux s'observent mutuellement d'une manière parfaitement symétrique. C'est à partir du moment où l'un d'eux change de référentiel inertiel que les explications d'Einstein deviennent obscures, alors que celles de Lorentz demeurent très claires. En particulier, le décalage horaire de Lorentz s'inverse (+bêta * x) au moment où le jumeau B fait demi-tour. Celui-ci observe donc que l'horloge de A reprend une énorme avance en peu de temps, de manière à pouvoir continuer de prendre du retard jusqu'à son arrivée. |
LE PARADOXE D'EHRENFEST
|
Paul Ehrenfest a présenté en 1909 une objection majeure : la circonférence d'un disque ne correspond plus à 2 * pi * R s'il tourne sur lui-même à grande vitesse. Sa géométrie devient donc incohérente et inexplicable. Le Scanner du Temps lève le voile sur ce que la Relativité n'arrivait pas à expliquer de manière raisonnable. Il montre que ce n'est pas l'espace qui se transforme, c'est plutôt la matière, qui peut fort bien s'adapter à la contraction qu'elle subira. La discontinuité. En effet, contrairement à l'espace théoriquement parfait de la Relativité, qui ne saurait se dissocier, la matière d'un disque est hautement malléable et adaptable. Dans le pire des cas elle se disloque tout simplement si les conditions l'y obligent. Si le disque tourne, ses différentes parties devraient se dissocier en laissant des espaces vides. La figure ci-dessous montre que plus les parties sont petites, moins elles subissent de "distorsion angulaire". La distorsion angulaire. Tout se passe comme si un seul ou plusieurs plans de symétrie attiraient vers eux chacune des molécules de ces parties, en fonction de leur distance, et le long d'un arc de cercle. Il en résulte une distorsion angulaire qui est d'autant plus sévère que le nombre de plans de symétrie et donc de sections est petit. Une seule section produit une forme cardioïde, alors que plusieurs produisent plutôt une forme lancéolée, la pointe étant dirigée vers le centre. On pourrait parler de "distorsion foliaire" car l'ordinateur montre systématiquement des formes qui rappellent les feuilles typiques d'un grand nombre de plantes : |
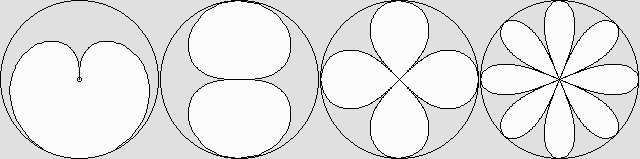
La distorsion angulaire ou "foliaire", qui produit des espaces vides.
À la périphérie du disque, la vitesse atteint celle de la lumière.
La contraction y est infinie et aucune matière ne peut donc y exister.
|
Ces figures montrent que la contraction de la matière d'un disque rotatif doit se traduire par des espaces vides, d'où la discontinuité associée depuis le début au paradoxe d'Ehrenfest. Si la substance du disque était liquide ou gazeuse, il pourrait très bien ne pas se produire de dissociation, puisque les molécules sont entourées de vide et s'entrechoquent en raison de la chaleur. Elles peuvent facilement se réorganiser. Mais autrement, la matière du disque devrait se séparer en autant de parties que son élasticité le permet, en laissant des espaces vides, de préférence près d'un plan radial. Chacune de ces parties devrait se contracter selon l'arc de cercle qu'elle décrit, puisque son déplacement ne s'effectue pas sur une trajectoire rectiligne. Bien évidemment, une telle situation est pratiquement impossible à réaliser en raison de la force centrifuge, sauf peut-être en présence d'une gravité phénoménale. Les ondes sont des causes qui produisent des effets. Il faut réaliser que toutes les forces sont des causes qui sont attribuables à des ondes. On peut proclamer que toutes les causes sont des ondes et qu'elles agissent à la vitesse de la lumière. Les causes qui naissent simultanément produisent des effets qui sont retardés différemment en fonction de la vitesse relative de la lumière. Les délais ne sont pas les mêmes vers l'avant et vers l'arrière et leurs effets s'échelonnent donc dans le temps. Il ne se produit en réalité qu'une distorsion dans les rapports de cause à effet. Pour corriger cette distorsion, la partie arrière d'une roue qui roule à grande vitesse doit être en avance sur la partie avant, de manière à ce que quelqu'un placé au centre puisse observer une simultanéité virtuelle et même en dépendre. Comme l'a écrit Lorentz lui-même, ces considérations sur le temps et l'espace sont purement mathématiques et artificielles. Ce qu'il faut comprendre, c'est que les transformations de Lorentz se produisent pour des raisons mécaniques, et non pas parce que la matière doit se conformer à des équations. On parle donc ici de la mécanique du mouvement. Et puisqu'il est question de mécanique, parlons d'engrenages. Des engrenages à pignon et crémaillère. La mécanique de toutes sortes de machines fait appel à des engrenages. Léonard de Vinci et James Starley (l'inventeur de la direction à pignon et crémaillère) auraient été vivement intéressés par l'animation montrée ci-dessous, mais je crois bien que les ingénieurs actuels devraient également l'observer avec le plus vif intérêt. Il s'agit d'une roue dentée qui est actionnée par quatre crémaillères (au choix) faites de disques alignés sur une droite : À la périphérie de la roue dentée montrée ci-dessous, soit à l'extrémité des dents, la vitesse atteint celle de la lumière. À cet endroit, si elles étaient au repos, les dents seraient carrées. Mais en raison de la distorsion foliaire expliquée plus haut, leur largeur se rétrécit progressivement jusqu'à devenir nulle. Par contre, au niveau des disques des quatre crémaillères, la vitesse est de 0,866 c. Ces disques sont donc contractés de moitié: ils affectent la forme d'une ellipse aplatie. Même la distance qui les sépare est réduite de moitié. Il s'agit tout simplement de respecter les transformations de Lorentz. Voici ce que le scanner du temps fait de cette roue dentée et des crémaillères à disques : |

À gauche, la roue dentée tourne, mais son centre est au repos dans l'éther.
À droite, le scanner la montre comme si elle roulait à 0,866 c sur une crémaillère au repos.
|
La partie droite de cette animation montre que le scanner du temps peut convertir sans difficulté n'importe quelle scène animée. Bien que ses différentes parties se déplacent à des vitesses et dans des directions différente, il peut montrer comment elles seraient transformées si l'ensemble se déplaçait à grande vitesse. D'ailleurs, si l'on inverse le processus, ce scanner peut reconstituer la scène telle qu'elle apparaissait avant la transformation. Une roue qui roule sur une surface réputée au repos dans l'éther peut se déplacer théoriquement à la vitesse de 0,866 c. Contrairement à ce qu'on serait enclin à penser, sa partie supérieure n'avance pas au double de cette vitesse, soit 1,732 c. On constate que c'est plutôt la loi de l'addition des vitesses de Poincaré qui s'applique : bêta'' = (bêta + bêta') / (1 + bêta * bêta') Les deux vitesses étant de 0,866 c, on obtient une vitesse totale de 0,9897 c de manière à respecter la règle de Poincaré qui stipule qu'aucune matière ne peut atteindre la vitesse de la lumière. C'est pourquoi le scanner montre que les sphères qui se déplacent vers la droite, en haut et à droite de l'animation, sont très fortement contractées, soit selon 14 % de leurs dimensions normales. De deux choses l'une, ou le centre de la roue est au repos dans l'éther, et alors cette roue ressemble au diagramme animé de gauche ; ou le centre de la roue se déplace à la vitesse absolue de 0,866 c, et alors elle a vraiment la forme de la reproduction montrée à droite. En particulier, elle n'est plus circulaire. Sa circonférence est contractée de moitié selon le facteur de contraction g de Lorentz. Toutefois, et c'est là toute la magie de la Relativité, un observateur qui suivrait cette roue hautement déformée à la même vitesse la verrait tout simplement comme elle est montrée à gauche. Incroyable, direz-vous ? Sans doute, mais c'est pourtant exact car ça se calcule et ça se vérifie. Même l'espace entre les différents éléments se contracte. Pour éviter tout malentendu, il faut préciser que l'image de droite représente ce qu'il adviendrait de la roue et des cinq crémaillères si l'ensemble se trouvait accéléré par une force quelconque, la gravité par exemple. Dans ce contexte, on présume que certains éléments sont reliés entre eux, ce qui explique que l'espace entre les disques des crémaillères se contracte tout comme les disques eux-mêmes. Le passage d'un référentiel à un autre est purement théorique. Il est bien évident qu'aucune matière ne pourrait se transformer d'une manière aussi radicale. En particulier, la partie externe des roues, sur laquelle les dents sont fixées, est montrée sans espaces vides intermédiaires. Elle devrait être hautement élastique pour supporter une dilatation de ses molécules tout en refusant de se dissocier en sections plus petites. Dans ce cas, on pourrait penser que la roue entière devrait rétrécir à mesure qu'elle accélère, ou qu'elle grandisse plutôt à cause de la force centrifuge, à moins qu'une gravité très forte provenant de son centre ne vienne équilibrer ces deux forces. Mais d'un autre côté, il ne fait aucun doute que chacune des deux roues dentées montrées dans l'animation ci-dessous pourrait très bien exister dans son propre référentiel, pourvu qu'elle tourne à l'intérieur de limites acceptables. D'ailleurs, il existe des pulsars qui tournent sur eux-mêmes à des vitesses ahurissantes, et qui se déplacent aux confins de notre univers à des vitesses qui frôlent celle de la lumière. Leur configuration doit donc se conformer aux transformations montrées ci-dessous, à droite. Dans cette animation, on peut observer comment les crémaillères et les différents éléments du disque se comportent, avant et après leur transformation : |

Les transformations de Lorentz, dans toute leur splendeur.
À gauche, le disque est au repos. À droite, il se déplace vers la droite à 86,6 % de la vitesse de la lumière.
Supposez que vous êtes un ange, c'est à dire un observateur immatériel non transformé.
De plus, vous observez ces deux disques à l'aide d'une lumière surnaturelle dont la vitesse est infinie.
Alors c'est ainsi que vous les verriez. Il s'agit donc de leur aspect réel, absolu.
|
Notez bien : 1. Le disque de droite tourne deux fois plus lentement, conformément à la transformation temporelle de Lorentz, qui indique que les événement se déroulent plus lentement dans un système mobile. Il faut observer que les crémaillères verticales, par exemple, se déplacent sur l'axe y à 86,6 % de la vitesse de la lumière dans le système au repos, alors que leur vitesse est réduite de moitié dans le système mobile. En première analyse, la composition de leur vitesse devrait se faire selon le théorème de Pythagore, d'où une vitesse résultante atteignant 122 % de la vitesse de la lumière. Mais c'est impossible. On verra à la page sur la masse active et réactive que les chocs obliques et donc les composantes de force ne se font pas selon Pythagore, mais bien selon l'effet Doppler. Si un corps est accéléré sur l'axe x, il en sera ralenti sur l'axe y parce que la masse active subit une rotation. De son point de vue, des ondes transversales proviennent de l'avant, car elles doivent être inclinées selon l'angle thêta pour lui sembler être transversales. C'est pourquoi il dévie plus fortement vers l'axe x. L'effet Poynting-Robertson, par exemple, serait basé sur cette propriété ; mais il n'en est pas moins erroné, du moins selon cette explication, parce qu'il considère un corps qui décrit une courbe et non une droite. Ici, la vitesse sur l'axe y passera de 0,866 c à 0,433 c, soit selon le facteur g. La vitesse résultante absolue des crémaillères verticales sera de 0,968 c, cette fois-ci selon Pythagore, et la contraction des disques sur l'image de droite est donc de 0,25. Leur direction absolue comparativement à l'axe x vaut : arc tan (0,433 / 0,866), soit 26,56°. 2. On présume que la roue dentée de gauche tourne à raison d'un tour par seconde. Sa circonférence vaut une seconde-lumière, soit 300 000 km, et c'est pourquoi sa vitesse atteint celle de la lumière. Le rayon de la roue vaut donc 300 000 / 2 p = 47 746 km. 3. S'ils ne se déplaçaient pas, tous les disques auraient le même aspect que le disque central de la roue montrée à gauche. La largeur des dents de la roue correspond aussi au diamètre de ce disque ; mais à cause de la distorsion angulaire, cette largeur diminue progressivement jusqu'à devenir nulle aux extrémités. 4. La "crémaillère auxiliaire" additionnelle montrée au bas de l'image de gauche se déplace vers la gauche à 99 % de la vitesse de la lumière (0,98974 c selon la loi de l'addition des vitesses de Poincaré montrée plus haut). J'ai eu un peu de difficulté à l'ajouter au programme qui a produit cette animation, mais je tenais absolument à montrer que le scanner du temps pouvait se jouer de toutes les situations. En effet, il peut traiter des vitesses relatives approchant le double de la vitesse de la lumière. 5. À gauche, la crémaillère du haut se dirige vers la droite à 0,866 c, mais sa vitesse n'atteint pas le double dans l'image de droite. C'est encore une fois en raison de la loi de l'addition des vitesses de Poincaré, et toujours à cause de l'accélération d'un corps, qui se fait selon l'effet Doppler. La vitesse de la crémaillère supérieure montrée à droite est ainsi de 0,98974 c et la contraction de ses disques atteint donc aussi peu que 0,14 fois leur diamètre original, selon le facteur g. C'est également le cas de la crémaillère auxiliaire montrée au bas de l'image de gauche. 6. L'image de gauche montre une roue au repos et une crémaillère auxiliaire qui se déplace vers la gauche. L'image de droite montre plutôt une crémaillère auxiliaire au repos et une roue qui se déplace vers la droite à la vitesse de 0,866 c. Mais puisque "l'observateur immatériel non transformé" doit suivre la roue pour l'observer, la crémaillère au repos semble se déplacer vers la gauche à la vitesse de 0,866 c. En réalité, elle est au repos et c'est pourquoi elle n'est pas contractée. 7. Dans ce cas très particulier d'un objet au repos qui semble se déplacer parce qu'il est vu à partir d'un repère mobile, il n'est pas question de faire intervenir la loi de l'addition des vitesses de Poincaré. La matière et celui qui l'observe se transforment vraiment, et même si cet observateur matériel transformé a l'impression que c'est plutôt la matière au repos qui se transforme, celle-ci ne se transforme pas dans les faits. Il faut garder à l'esprit que les faits sont absolus, et que la Relativité est le résultat d'une mystification. 8. Puisque la vitesse de la crémaillère inférieure passe de 0,866 c à 0 c, celle de la crémaillère auxiliaire passe de 0,98974 c à 0,866 c vers la gauche selon la loi de l'addition des vitesses. Mais puisque le système se déplace plutôt vers la droite à cette même vitesse, la vitesse relative de cette crémaillère vaut réellement le double, soit 1,732 c. Dans les faits, comparativement à un autre objet qui se déplace dans l'autre sens, un objet mobile peut atteindre une vitesse relative approchant le double de la vitesse de la lumière. Mais il faut pour cela que le phénomène soit observé à partir d'un référentiel au repos intermédiaire. C'est une chose que la Relativité d'Einstein n'admet pas, mais qui pourtant est très possible. Pour agir simultanément en un point donné, s'il est mobile, les ondes qui proviennent de l'arrière devront avoir parcouru une plus grande distance à cause de son déplacement. D'un point de vue mécanique, la seule manière de compenser la différence est de prendre de l'avance à l'arrière et du retard à l'avant. Comme on le voit ci-dessus, même des engrenages doivent se conformer à cette règle. |
LE SCANNER DU TEMPS PERMET DE REPRODUIRE MON ÉLECTRON MOBILE.
|
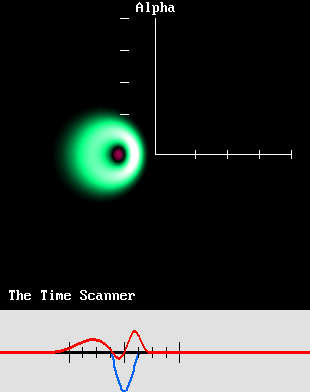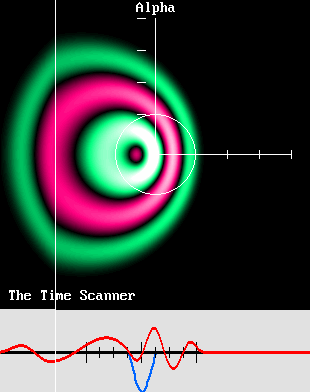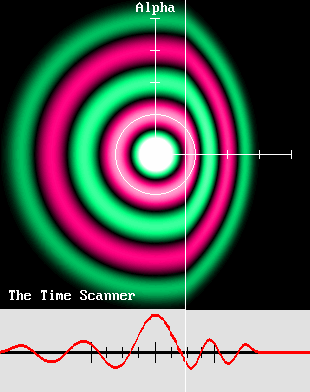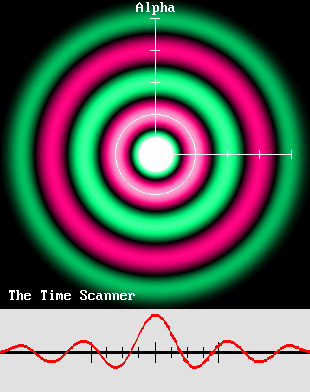
J'ai inventé le Scanner du Temps en mars 2004. C'était bien après avoir produit des animations de mon électron mobile, que j'ai rendu public fin 2001, et dont les premières versions furent assez difficiles à réaliser. J'ai donc été à la fois consterné et enchanté de constater que la méthode du scanner permettait de reproduire cet électron mobile beaucoup plus facilement. Pourtant je n'étais pas encore au bout de mes surprises, car j'ai finalement compris que cet électron pouvait encore plus facilement être reproduit à l'aide des équations de Lorentz, comme le montre ce programme : Ether17.exe Ether17.bas Puisque le Scanner du Temps provoque un effet Doppler particulier qui se révèle conforme aux transformations de Lorentz, il peut montrer comment des ondes stationnaires sphériques et concentriques seront transformées. Il suffit de balayer une animation de ces ondes en sens contraire de leur déplacement présumé. Les images ci-dessous ont été réalisées en adoptant une vitesse d'impression plus lente que la vitesse de balayage: |
|
|
Le scanner du temps peut reproduire l'image de mon électron mobile à partir d'un électron au repos.
|
|
Inversement, le scanner du temps peut reproduire l'image d'un électron au repos à partir d'un électron mobile.
Ces deux animations montrent d'une manière spectaculaire que les transformations de Lorentz sont réversibles.
Cela signifie que si nous nous déplaçons à travers l'éther, nous ne pouvons pas déceler l'effet Doppler.
Tout se passe comme si nous étions au repos, conformément à la loi de la Relativité.
LE BALAYAGE EN SENS INVERSE
|
L'animation ci-dessus montre que si l'on inverse le sens du balayage, l'effet Doppler est annulé au lieu d'être provoqué. Il faut rappeler que ces vitesses ont été établies conformément aux équations de Lorentz. Or ces équations telles que présentées par Henri Poincaré sont réversibles. Elles montrent que même si un système se déplace à travers l'éther, il aura l'apparence d'un système au repos. Il faut bien préciser ici qu'il ne s'agit que des apparences, puisqu'un électron qui se déplace subit réellement l'effet Doppler. De la même manière, l'animation ci-dessous montre deux ondes sphériques de l'électron mobile, l'une réputée convergente et l'autre divergente. Si l'électron est au repos, ces ondes se croisent partout simultanément. Or si l'électron se déplace, ce n'est plus le cas. Mais à cause du décalage horaire tout se passe comme si elles continuaient de se croiser simultanément. Là aussi le scanner se déplace vers la droite, et il annule ainsi l'effet Doppler. On remarque que le principe de Huygens (selon les célèbres ondelettes) continue de s'appliquer même si le système se déplace. Tout indique que Lorentz le savait, car il a signalé à Michelson qu'il devait se produire une aberration angulaire dans son appareil, et qu'il fallait en tenir compte dans les calculs. Même si elles sont sphériques, les deux ondes se croisent sur un ellipsoïde aplati selon Lorentz. On constate aussi qu'au moment où le scanner atteint le point central, le rayon de ces deux ondes est le même tout en étant plus grand que le grand rayon de l'ellipse. Il y a donc contraction même sur un axe transversal, mais le ralentissement de la fréquence de ce système, que Lorentz prévoit, entraînera une augmentation de la longueur d'onde. Alors les dimensions de l'ellipsoïde seront finalement conformes aux prévisions de Lorentz et de Poincaré : |
|
|
Le scanner synchronise l'onde convergente et l'onde divergente qui subissent l'effet Doppler.
Tout se passe comme si ces ondes se croisaient sur un ellipsoïde (en vert) au même instant.
On constate aussi que les ondelettes de Huygens parviennent au centre au même instant.

Ces images réalisées par M. Philippe Delmotte montrent sensiblement le même phénomène, en beaucoup mieux.
LA CAMÉRA NUMÉRIQUE À SCANNER
|
La caméra montrée ci-dessous était décrite dans mon ouvrage optique des miroirs. Il s'agit peut-être d'une de mes nombreuses inventions, pour lesquelles je n'ai pas fait de demande de brevet. Je n'en ai pas les moyens. D'ailleurs cette caméra ne semble pas intéressante d'un point de vue commercial. Elle pourrait toutefois le devenir si la sensibilité des scanners devenait un jour beaucoup plus grande. On peut en effet transférer les charges des photosites CCD de l'un à l'autre à la même vitesse que celle de leur défilement. La caméra utilise un miroir Mangin sphérique achromatique (peut-être aussi l'une de mes inventions), dont le champ à très grand angle est courbé mais parfaitement libre de toutes les aberrations du premier ordre : coma, astigmatisme, aberration de sphéricité et aberration chromatique. Je ne considère pas la courbure de champ comme une aberration, bien au contraire. Cette caméra comporte aussi une sphère rotative munie de huit scanners courbés : |
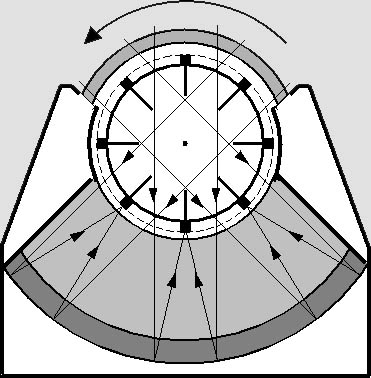
La caméra numérique à scanners rotatifs.
|
S'il y a huit scanners, il faut trois tours par seconde pour obtenir les 24 images classiques du cinéma. C'est pourquoi il faudrait des scanners beaucoup plus sensibles que ceux qu'on fabrique actuellement. Toutefois ceci ne nous empêche pas d'analyser les propriétés étonnantes de cette étrange caméra. De toute évidence, ce mécanisme à scanners devrait produire les mêmes effets que le Scanner du Temps. Ceci signifie par exemple qu'en filmant (lentement) les vagues circulaires et concentriques que produit un caillou lancé dans l'eau tranquille d'un étang (ci-dessous, à gauche), on obtiendrait un effet Doppler (à droite) : |
|
|
|
L'effet Doppler.
|
C'est ce que l'animation montrée au début de cette page montre clairement. En fait, à la condition de respecter la vitesse de balayage et la vitesse d'impression requise (ou de déplacement, ce qui suppose une caméra à un seul scanner qui tourne sur un pivot et filme sur 360°), cette caméra devrait produire les trois effets bien connus des transformations de Lorentz. Les animations de M. Serge Cabala. Voici le site de M. Cabala : On trouvera sur ce site des animations très intéressantes montrant entre autres un euro qui tourne sur lui-même et une machine à piston avec sa roue à erre. Ces images semblent étrangement déformées, mais l'animation montrée plus haut confirme qu'il s'agit bien de la distorsion prévue par Lorentz. On trouvera aussi sur ce site une section historique très intéressante sur l'époque de Lorentz. Dès 1975, et peut-être avant, M. Cabala fut la première personne sur cette planète à parler de la nature exclusivement ondulatoire de la matière. Il précise d'ailleurs que Lorentz lui-même parlait de la matière comme si elle résultait d'une déformation locale quelconque de l'éther. C'est bien ce que font les ondes stationnaires sphériques. Il a aussi montré que la Relativité était en faveur de l'éther à une époque où ce mot avait très mauvaise presse. Je tiens donc à souligner et à glorifier l'intelligence et le courage dont il a fait preuve face à une meute d'ignorants. D'autres animations qui montrent le Scanner du Temps à l'œuvre. Vous
trouverez un peu partout dans ces pages des programmes et des animations
qui offrent un aperçu de ce dont le Scanner du Temps est capable. J'en
ai fait une liste ci-dessous, qui ne figurent pas sur la présente page,
mais elle n'est pas exhaustive.
Bradley_Aberration_Parallax_Scan.mkv Le
programme : Bradley_Aberration_Parallax_Scan.bas
Bradley_Aberration_Parallax_Scan.exe Bradley_Aberration.5c_Scan.mkv Le programme : Bradley_Aberration.5c_Scan.bas Bradley_Aberration.5c_Scan.exe Le programme : WaveMechanics07.bas WaveMechanics07.exe
La mécanique du mouvement. Ce n'est qu'en l'an 2009 que j'ai réalisé que ces pages contenaient de nombreuses observations qui concernent une toute nouvelle science dont j'avais jeté les bases sans le savoir : la mécanique du mouvement. On se rappellera que Henri Poincaré (1904 et 1905) et Albert Einstein (1905) ont publié des traités "sur l'électrodynamique des corps en mouvement", qui ont fait époque. Le problème, c'est qu'ils étaient fondés sur les ondes dites "électromagnétiques" et sur les équations de Maxwell. Or de telles ondes n'existent pas, ce qui signifie que les équations de Maxwell ne sont que du vent. Il ne s'agit que d'un calcul prétentieux (on a prétendu que c'était vrai sans en faire la preuve) sur les champs électriques et magnétiques qui sont présent dans la matière lors de l'émission des ondes radio, et qu'on retrouve miraculeusement dans la matière à la réception. Il est faux de prétendre qu'ils voyagent de l'un à l'autre. J'affirme ici que la lumière et les ondes radio n'ont rien "d'électromagnétiques" tant qu'elles se propagent dans le vide. Il s'agit purement et simplement d'ondes longitudinales normales qui se propagent dans l'éther, sachant que les ondes ne peuvent exister sans la présence d'un médium. À l'émission, ces ondes sont provoquées par les oscillations des électrons, ce qui déclenche localement des phénomènes électromagnétiques. Les ondes composites qui en résultent déclenchent à leur tour des phénomènes électromagnétiques identiques en atteignant ou en traversant la matière, ce qui explique très bien pourquoi la matière, en particulier une antenne, peut tout aussi bien capter des ondes qu'en émettre. Sachant que la matière reçoit et émet constamment des ondes, j'ai réalisé en juin 2005 que toutes les forces qui interviennent dans la mécanique de la matière ont pour origine les ondes stationnaires causées par la rencontre de ces ondes. Il s'agit des champs de forces, dont l'action concerne une autre science toute nouvelle, la dynamique des champs de force. Si le mouvement intervient, et c'est toujours le cas s'il est question de mécanique, ces ondes présentent un effet Doppler. Or puisqu'il s'agit en réalité des transformations de Lorentz, on assiste alors à une contraction des champs de force et de la structure de la matière elle-même. Il est donc essentiel de tenir compte de l'effet Doppler et des transformations de Lorentz pour évaluer les effets de l'action et de la réaction. J'ai déjà montré qu'il faut faire intervenir des masses et des forces actives et réactives. Poincaré et Einstein auraient donc du intituler leurs traités plus simplement: "Sur la dynamique des corps en mouvement." L'optique du mouvement. En 2009, j'ai aussi jeté les bases d'une nouvelle science qui révolutionnera la physique : l'optique du mouvement. Puisqu'il est question de mouvement, elle devra tenir compte de l'effet Doppler et des transformations de Lorentz. Cette nouvelle science fera intensivement appel au médium virtuel inventé par M. Philippe Delmotte en juin 2005 et simplifié par M. Jocelyn Marcotte en janvier 2006. Dans les circonstances, il s'agissait là d'une invention majeure, capitale. Ce sera un outil extrêmement puissant qui nous permettra de découvrir comment la matière fonctionne. Bien entendu, cette science fera aussi appel au Scanner du Temps. C'est qu'il n'existe pas d'autre manière de montrer comment un observateur en mouvement perçoit un phénomène optique dans son environnement. Étrangement, il perçoit un effet Doppler dans les ondes d'un système au repos, même si cet effet Doppler n'existe pas. Mais il n'en perçoit pas dans les ondes qui sont émises dans son propre environnement, et qui pourtant sont bel et bien affectées par l'effet Doppler. On peut le comprendre facilement parce que, à distance égale, les événement qu'il voit à l'avant se sont déroulés plus tard qu'à l'arrière. En introduisant ou en corrigeant cette distorsion, le Scanner du Temps permet donc de montrer très facilement les deux côtés de la médaille. Un observateur mobile perçoit même une contraction dans la structure de la matière au repos alors que c'est plutôt lui qui est contracté. C'est normal car la matière elle-même est soumise à l'effet Doppler puisqu'elle est faite d'ondes. L'étude de la matière relève donc de l'optique. La physique atomique, c'est désormais l'affaire des opticiens. Cela nous permettra de mieux comprendre la véritable Relativité, celle de Lorentz, qu'on abordera à la page suivante. |
| 01 | 02 | 03 | 04 | 05 | 06 | 07 | 08 | Vous êtes ici. | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 |
|
Gabriel LaFrenière, Bois-des-Filion en Québec. Sur l'Internet depuis septembre 2002. Dernière mise à jour le 18 janvier 2010. Courrier électronique : veuillez consulter cet avis. La théorie de l'Absolu, © Luc Lafrenière, mai 2000. La matière est faite d'ondes, © Gabriel Lafrenière, juin 2002. |
ANTONIVS·MORO·BRVTVS·EST