L'ÉNERGIE CINÉTIQUE

Cette image animée représente une boule de billard qui en heurte une autre.
Le processus fait intervenir un champ de force intermédiaire et des masses actives (a) et réactives (r).
L'énergie cinétique telle que formulée par Poincaré et Einstein correspond au gain de masse prédit par Lorentz :
E = (gamma – 1) m c 2
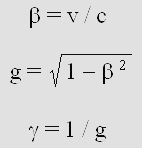
Si la vitesse est très grande, l'ancienne formule newtonienne s'avère inexacte à cause de la division par deux :
E = m v 2 / 2
Toutefois, j'ai pu la rendre exacte :
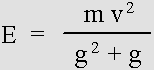
Cette formule dérive clairement de la formule newtonienne.
Il suffisait de tenir compte de l'augmentation de la masse indiquée par Lorentz.
Cela montre que Newton n'avait pas tout à fait tort et que nous aurions intérêt à mettre à jour sa mécanique.
![]()
![]() Page d'accueil :
La
matière est faite d'ondes.
Page d'accueil :
La
matière est faite d'ondes.
LE CALCUL DE L'ÉNERGIE CINÉTIQUE SELON NEWTON
|
Toute la mécanique de la matière dépend de l'énergie cinétique. Celle-ci fait référence au mouvement : sans lui, il n'y aurait pas de mécanique. En fait, puisque le temps est la mesure d'un mouvement donné dans un espace donné, il n'y aurait même pas de temps. D'un autre côté, toutes les forces sont attribuables à des ondes et la matière elle-même est faite d'ondes. Dans ces conditions, la mécanique de la matière, c'est forcément la mécanique des ondes. Or en présence d'ondes et de mouvement, l'effet Doppler est incontournable. Ces pages montrent hors de tout doute que les transformations de Lorentz ne sont rien d'autre et rien de plus que la formulation de l'effet Doppler que les ondes de la matière subissent. Elles montrent aussi que que si la masse de la matière augmente avec sa vitesse comme l'a montré Lorentz, c'est précisément à cause de l'effet Doppler. Nous allons maintenant vérifier pourquoi l'énergie cinétique correspond tout simplement à cette augmentation de masse. Nous allons voir aussi que, contrairement à ce que la théorie de la Relativité d'Einstein laissait croire, les lois de Newton demeurent remarquablement pertinentes. Mais il est clair qu'elles ont besoin d'un certain remaniement pour redevenir tout à fait justes.
L'énergie cinétique à l'œuvre. Chacun sait que lorsque deux sacs de sable sont projetés l'un contre l'autre, ils ne subissent pas l'effet de recul normal des balles de caoutchouc ou des boules de billard. Dans ce cas, l'énergie cinétique est convertie en chaleur, l'exemple le plus spectaculaire étant celui d'une énorme météorite qui atteint le sol. Alors elle fond littéralement. Pour tenir compte de la totalité de l'énergie en termes d'énergie cinétique, il convient de parler plutôt d'un choc élastique, l'exemple typique étant celui des deux boules de billard montrées ci-dessus. Dans ce cas, ce sont les électrons présents à la périphérie des molécules qui exercent une force répulsive. C'est qu'à l'échelle d'un atome, ils viennent alors plus près les uns des autres que les protons. C'est donc le champ électrostatique qui agit. On aura vu à la page sur la force de Coulomb que ce champ de force est fait d'ondes stationnaires très particulières, et que ces ondes contiennent de l'énergie.
Le champ de force électrostatique est fait d'ondes stationnaires.
Le champ électrostatique, tout comme le champ gluonique, c'est de l'énergie cinétique "en conserve". C'est un champ de force, qui agit sensiblement comme un ressort qu'on tend. Puisqu'il doit composer avec le mouvement, il est fait "d'ondes stationnaires mobiles". Cette énergie se transmet à la vitesse des ventres et des nœuds de ces ondes stationnaires, qui est toujours inférieure à celle de la lumière. L'énergie cinétique est alors transférée d'un objet à l'autre à cette vitesse par l'intermédiaire du champ de force. C'est en quelque sorte de l'énergie en transit.
Le calcul de l'énergie. Dans ce contexte, il convient de revoir d'abord le calcul de l'énergie cinétique. Tous connaissent bien l'ancienne formule élaborée selon la mécanique de Newton : E = m v 2 / 2 Il faut savoir que l'énergie E s'évalue en joules, la masse m en kilogrammes, les distances en mètres et la vitesse v ou c en mètres par seconde. Cette équation n'est pas de Newton : elle a été mise en avant par Émilie Du Châtelet, mais il est clair que la célèbre conjointe de Voltaire s'appuyait sur des calculs élaborés avant elle, en particulier par Leibniz. Puisque ce dernier a également participé à la création du calcul différentiel à la même époque que Newton, il convient de lui rendre hommage ici, en toute justice. Cette formule peut être facilement synthétisée à partir des deux équations de base de la mécanique de Newton. On en donne le cheminement dans les manuels de physique.
Cette formule comporte deux erreurs. On sait depuis plus d'un siècle que cette formule devient inexacte pour des vitesses qui ne sont plus négligeables devant la vitesse de la lumière. C'est que la masse d'un objet augmente avec sa vitesse selon le facteur gamma. On peut considérer que c'est l'une des transformations de Lorentz : en effet, c'est Lorentz lui-même qui l'avait prédit, ce même facteur indiquant du même coup le ralentissement des horloges et la contraction des distances. Puisque la masse m est celle de la matière au repos, il faut d'abord distinguer par la majuscule la masse totale M de la matière en mouvement, qu'on obtient facilement grâce au facteur gamma : M = gamma * m La masse de la matière, qui est par définition la mesure de son inertie (mais aussi de son énergie), augmente donc selon sa vitesse. Par exemple, à 86,6% de la vitesse de la lumière, la masse d'un objet double puisque dans ce cas le facteur gamma vaut 2 exactement. Si elle était au départ de 1 kg, elle passe à 2 kg. C'est ainsi qu'après le choc, la boule de billard de droite montrée dans l'animation ci-dessus a pris de la vitesse. Elle est donc assujettie aux transformations de Lorentz. En particulier, elle s'est contractée de moitié sur l'axe du déplacement selon le facteur de contraction de Lorentz. Et comme l'indique la formule ci-dessus, sa masse a doublé selon l'inverse, c'est à dire le facteur gamma. Son inertie étant doublée, le fait d'appliquer de nouveau à cette boule de billard la même quantité d'énergie cinétique ne peut pas doubler sa vitesse. C'est ce qui explique qu'elle ne pourrait jamais atteindre la vitesse de la lumière. La nouvelle vitesse correspond plutôt à la loi de l'addition des vitesses élaborée par Henri Poincaré : V3 = (V1 + V2) / (1 + V1 * V2) Après application de la même force, la vitesse de la boule passera de 0,866 c à 0,9897 c avec : V1 = V2 = 0,866
Prenons un exemple. On retiendra cet exemple pour les fins de la démonstration qui suit : La vitesse normalisée bêta = v / c = sin 60° = (1 – g 2) 1 / 2 = 0,866 La vitesse de la lumière, arrondie pour simplifier : c = 300 000 000 m/s (299 792 458 m/s). La vitesse d'entraînement : v = bêta * c = 259 807 621 m/s Le facteur gamma = 1 / (1 – bêta 2) 1 / 2 = 1 / g = 2 Le facteur de contraction de Lorentz : g = (1 – bêta 2) 1 / 2 = 1 / gamma = 0,5 La masse de la matière lorsqu'elle est au repos : m = 1 kg Sa masse totale lorsqu'elle se déplace : M = gamma * m = 2 kg Le gain de masse : G = gamma * m – m = (gamma – 1) m = 1 kg L'énergie intrinsèque de la matière au repos : E = m c 2 = c 2 = 9 * 10 16 joules.
1 – Il faut tenir compte de l'augmentation de masse. Il s'agit de modifier l'ancienne formule newtonienne de manière à tenir compte de l'augmentation de la masse. En premier lieu, il faut donc appliquer le facteur gamma de la manière suivante : E = m v 2 / 2 devient : E = gamma * m v 2 / 2 Or on constate que c'est toujours inexact. Poincaré (et Einstein ?) en est plutôt arrivé à ceci : E = (gamma * m – m) c 2 ou encore : E = (gamma – 1) m c 2 On trouve que le gain de masse vaut : G = gamma * m – m = 1 d'où : E = G c 2 = c 2 = 9 * 10 16 joules. On voit que dans cet exemple, l'énergie cinétique correspondant à un kilogramme de gain de masse est égale à l'énergie intrinsèque d'un kilogramme de matière au repos. Or on a vu que ce n'est pas encore ce qu'indique notre formule partiellement modifiée et il est évident que le problème se situe dans la division par deux.
2 – Il faut tenir compte de l'énergie de freinage. C'est qu'à faible vitesse, la réaction est égale à l'action. La moitié de l'énergie mise en œuvre est utilisée pour freiner une boule de billard mobile si elle en heurte une autre identique de plein fouet. L'autre moitié seulement pourra être utilisée pour accélérer l'autre boule. Il n'y a là rien de nouveau : c'est une simple application de la mécanique originale de Newton, qui indique qu'il faut de l'énergie aussi bien pour ralentir un corps que pour l'accélérer. Comme on l'a vu plus haut, l'énergie effective correspond dans ce cas à la moitié de l'énergie présente : E = gamma * m v 2 / 2 Par contre, la masse totale M = gamma * m d'un objet devient énorme comparativement à sa masse au repos si sa vitesse frôle de très près la vitesse de la lumière. Par exemple, si le facteur gamma est supérieur à 1000, la masse totale M de la boule de billard dépasse 1000 kilogrammes alors que l'énergie requise pour en immobiliser un seul kilogramme demeure inchangée. Elle devient négligeable en comparaison. Dans ce cas, l'énergie cinétique effective correspond pratiquement à la totalité de la masse : E = gamma * m v 2 / 1 E = M v 2 Avouez que ceci suggère fortement la célèbre formule E=mc^2. On en déduit que la division par deux doit évoluer progressivement selon la vitesse d'un objet pour devenir une division par un (donc sans effet) si cette vitesse frôle la vitesse de la lumière. Or le facteur de contraction g de Lorenz évolue précisément de un à zéro en fonction de la vitesse, ce qui permet de forger une équation qui s'avère finalement exacte : E = gamma * m v 2 / (g + 1) E = m v 2 / (g * (g + 1))
La formule de l'énergie cinétique newtonienne revue et corrigée. Cette formule produit maintenant des résultats exacts peu importe la vitesse. E = m v 2 / (g 2 + g) = c 2 = 9 * 10 16 joules. Avec : m = 1 ; v = 259 807 621 m/s ; c = 300 000 000 m/s ; g = 0,5. À comparer avec la formule de Poincaré : E = (gamma – 1) m c 2
Ainsi donc, le plus raisonnablement du monde, et en mettant à profit nos nouvelles découvertes sur l'effet Doppler et la nature ondulatoire de la matière, nous avons réussi à mettre à jour un point capital de la mécanique de Newton. Il n'était vraiment pas nécessaire de la torpiller sans vergogne comme l'a fait Einstein. Le point important, c'est que cette nouvelle approche permet de mieux comprendre le processus : nous savons maintenant pourquoi il en est ainsi !
La matière de base est indestructible. Ces pages montrent que plus de 99% de la masse de la matière, même si elle est au repos, est constituée d'énergie cinétique. L'essentiel de cette énergie est prisonnière de ces champs de force très puissants que sont les champs gluoniques, comme on le montre à la page sur les quarks et sur le proton. Il faut donc remettre les pendules à l'heure et affirmer haut et clair que l'énergie que la matière contient peut difficilement être libérée, et surtout pas en totalité. Il se peut pourtant qu'on découvre un jour une manière simple et propre d'en extraire des quantités significatives. Je pense par exemple que les électrons et les positrons qui forment un quark peuvent sans doute se rapprocher l'un de l'autre puis s'éloigner périodiquement dans un mouvement de va-et-vient (on parle également du "confinement" des quarks, qu'on pourrait dissocier de la même manière). Cela ne peut se faire que selon une certaine fréquence, toujours la même. Si cette fréquence était connue, il serait donc possible théoriquement de dissocier les électrons (ou les quarks) par résonance et de libérer toute l'énergie des champs gluoniques impliqués. Mais nous sommes encore très loin de pouvoir maîtriser une telle technologie. D'une part, un atome de fer est fait à plus de 99% de champs gluoniques remarquablement stables. On sait qu'il est possible de le fractionner ou d'en tirer des atomes plus lourds, mais cela ne peut en aucun cas libérer de l'énergie : pour y arriver, il faut plutôt dépenser de l'énergie. D'autre part, deux atomes de deutérium contiennent dans leur proton et leur neutron beaucoup plus d'énergie qu'après leur fusion en hélium, essentiellement sous forme de champs gluoniques. C'est cet excédent d'énergie qui est libéré dans le cas de la fusion nucléaire. Mais les atomes plus lourds que le fer présentent de nouveau une masse supérieure toutes proportions gardées. Ceux qui sont particulièrement instables, le plutonium par exemple, peuvent de nouveau libérer de l'énergie lors de la fission. Le "défaut de masse" correspond donc à un renforcement ou un affaiblissement des champs gluoniques, qui sont pour ainsi dire de l'énergie cinétique en conserve sous forme d'ondes stationnaires. Les électrons et les positrons, qui constituent moins de 1% de la masse de la matière à l'intérieur des quarks, sont sans doute indestructibles. On parle d'annihilation lorsqu'on les met en présence, mais j'ai toutes les raisons de penser qu'on a sauté un peu vite aux conclusions dans le but d'expliquer le formidable dégagement d'énergie, qui ne peut provenir que de la destruction du champ gluonique. Leur énergie relative étant minime, ils passent alors inaperçus dans le processus. D'un autre côté, un grand nombre d'électrons et de positrons dispersés au hasard dans l'espace doivent fatalement s'attirer mutuellement et augmenter fortement leur vitesse avant de s'enclencher l'un dans l'autre sous l'effet du champ gluonique. Ils amasseront éventuellement toute l'énergie de la matière, puisqu'ils sont en mesure de former spontanément des quarks, puis des protons uniquement à l'aide de l'énergie cinétique qu'ils tireront d'abord des champs électrostatiques, puis des champs gluoniques beaucoup plus puissants.
Ici, avant l'amplification, l'électron et le positron vibrent selon un décalage d'un quart de période. Le champ gluonique résulte d'une forte amplification des ondes stationnaires présentes sur l'axe. Bien plus faibles en comparaison, les deux particules passent alors inaperçues et l'ensemble devient un quark.
L'énergie a un lien avec la vitesse de la lumière. Ainsi donc, si le gain de masse est d'un kilogramme, l'énergie cinétique correspondante vaut tout simplement : E = c 2 E = 9 * 10 16 joules. Selon notre exemple, ce serait l'énergie cinétique d'une boule de billard qui se déplace à la vitesse de 0,866 c et dont la masse au repos est d'un kilogramme. Bien évidemment, une telle quantité d'énergie à une telle vitesse se traduirait dans les faits par une destruction complète des deux boules de billard ! Cette nouvelle approche confirme une fois de plus la validité de la célèbre équation : E = m c 2. Bien sûr, ce n'est pas une surprise, mais il faut tout de même souligner le fait que l'énergie de la matière a un lien avec la vitesse de la lumière. Il serait peut-être temps qu'on en prenne conscience. S'il en est ainsi, c'est tout simplement parce que la vitesse des ondes qui circulent dans l'éther est la même que celle de la lumière. Bien sûr, ce n'est pas seulement la lumière qui est concernée, ce sont toutes les ondes qui sont présentes dans l'éther, et cela inclut la matière elle-même.
Un deuxième exemple. Pour ceux qui auraient des doutes, voici une équation qui produit systématiquement un gain de masse G de 1 kg quelle que soit la masse au repos m. Le facteur de contraction g vaut alors : g = m / (m + 1) Par exemple, on obtient un facteur de contraction g de 0,2 si la masse au repos m ne vaut que 0,25 kg. Alors elle est augmentée à : M = 1,25 kg, et le gain de masse G sera donc là aussi d'un kilogramme exactement. Dans ce cas, la vitesse normalisée bêta vaut : bêta = (1 – g 2) 1 / 2 bêta = 0,979795897 v = bêta = 293938769 m/s m = 0,25 kg g = 0,2 E = c 2 = 0,25 v 2 / (0,2 2 + 0,2) = 9 * 10 16 joules.
Henri Poincaré et l'énergie cinétique. Parce que la masse totale est doublée à la vitesse de 0,866 c, on a vu que l'énergie cinétique d'un objet accéléré à cette vitesse devient égale à l'énergie de sa masse au repos. On est alors en présence de deux grandeurs d'énergie identiques, qui se dissimulent à l'intérieur d'un même corps et qui possèdent les mêmes propriétés. De plus, elles se calculent chacune selon la vitesse de la lumière au carré, mais aussi selon l'effet Doppler comme je le montre à la page sur la masse active et réactive. Cela donne fortement à penser qu'il s'agit d'ondes dans les deux cas, et que ce sont sans doute les mêmes. Poincaré ne pouvait pas le savoir, mais on peut ainsi proclamer que les ondes responsables de la matière au repos sont de même nature que celles qui sont responsables de l'énergie cinétique. Toute inertie s'oppose à une force, et les deux sont complémentaires. Il s'agit bien d'ondes, et ces ondes véhiculent manifestement de l'énergie puisqu'elles appliquent une pression de radiation, donc une force. La masse étant à la fois une mesure de l'énergie et de l'inertie, on peut donc attribuer aux ondes de l'éther une masse équivalente. Or Poincaré a bel et bien donné l'équivalent de la formule d'Einstein (et avant lui) à propos de la masse équivalente des ondes de la lumière. Sachant que la matière est faite d'ondes, il faut désormais reconnaître que cette formule qu'il a donnée devient prioritaire et étrangement pertinente : m = E / c 2 et donc, bien évidemment : E = m c 2 M. Jules Leveugle signale lui aussi que, dès 1900, Henri Poincaré avait établi que le rayonnement électromagnétique possédait une inertie équivalente correspondant à cette fameuse équation. On constate qu'encore une fois, Poincaré avait damé le pion à Albert Einstein. Henri Poincaré a donné cette formule en considérant les ondes dites électromagnétiques. J'affirme que de telles ondes n'existent pas et qu'il s'agit plutôt des mêmes ondes qui sont responsables de la matière et des forces d'action et de réaction. Dans ces conditions, et même s'il n'en était pas vraiment conscient, sa proposition doit être ramenée en pleine lumière. Je n'ai pas en mains le texte de Poincaré, et j'ignore par quel cheminement il est arrivé à cette conclusion, mais j'ai toutes les raisons de croire que son raisonnement était aussi valable que celui d'Einstein. Il faut aussi remarquer qu'Einstein n'a fait que reprendre le corollaire, c'est à dire la réaction qu'un objet opposerait à cette inertie, en considérant son recul alors qu'il émet un rayon de lumière. Il n'y a pas là de quoi s'extasier. En fait, puisqu'il ne cite jamais Poincaré alors qu'on sait très bien qu'il le lisait attentivement, il y aurait plutôt lieu de s'en indigner.
Poincaré et l'augmentation de la masse. M. Serge Cabala (http://ondes-relativite.info/) signale d'ailleurs que Henri Poincaré a repris en 1905 les équations de Max Abraham concernant l'augmentation de la masse (et donc de l'énergie) de l'électron. C'est Lorentz qui a d'abord prévu cette augmentation, mais c'est Poincaré qui en est arrivé à l'équation qui est toujours en usage aujourd'hui : E = gamma * m c 2 Il est bien évident que si la vitesse de l'électron est nulle, le facteur gamma est égal à l'unité, et il peut être éliminé de l'équation. On obtient donc encore une fois la célèbre équation : E = m c 2
Les forces actives et réactives. Si elles sont observées d'un point au repos dans l'éther, donc d'une manière absolue, l'action et la réaction ne sont plus "de même grandeur" à cause de l'effet Doppler. Tous les champs de force contiennent de l'énergie qu'ils rayonnent vers la matière située dans deux directions opposées. Il en résulte une pression de radiation. Ainsi donc, avant d'examiner comment on pourrait redonner toute leur splendeur aux lois de Newton, il faut donc se mettre dans la tête que tout ceci ne dépend finalement que de l'effet Doppler, plus exactement celui de Lorentz qui se caractérise par une fréquence plus lente. Plus une onde est comprimée, plus sa force augmente. C'est ce que j'ai montré à la page précédente sur la masse active et réactive.
Les forces d'action et de réaction ne sont pas égales à cause de l'effet Doppler.
Maintenant que nous savons pourquoi la compression des ondes est aussi responsable de l'énergie cinétique, nous sommes en mesure de revoir les lois de Newton sur le mouvement. |
LES LOIS DE NEWTON
|
Tout ceci nous amène à revoir les trois lois de Newton sur la dynamique de la matière. Malheureusement, la mécanique de la matière fait intervenir une notion qui était inconnue de Newton. Il s'agit du gain de masse, qui se traduit par une inertie croissante devenant infinie à la vitesse de la lumière. On sait qu'il s'agit d'une découverte de Lorentz, mais c'est manifestement Poincaré qui en a saisi toute l'importance, du moins si l'on se fie à cette déclaration faite en 1904 :
Henri Poincaré et la "mécanique nouvelle".
Ce texte est on ne peut plus clair. Ce que je tente de finaliser ici, c'est cette "mécanique nouvelle" pressentie par Henri Poincaré. Ce dernier a d'ailleurs réussi à la résumer correctement en une seule phrase, et les travaux conjoints de Lorentz et de Poincaré en constituent une assez bonne évaluation. En fait, j'ai l'impression de n'avoir qu'à poser la clé de voûte (la matière est faite d'ondes) sur un édifice déjà construit.
La mécanique de Newton est récupérable. Je suis donc persuadé que les lois de Newton sur la dynamique de la matière peuvent être récupérées sans problème malgré le fait que la version absolue de la Relativité de Lorentz indique plutôt qu'elles sont tout à fait fausses. C'est que de son côté, Henri Poincaré a découvert que la vérité absolue nous échappera toujours totalement. C'est la base de la Relativité. Nous n'avons pas le choix : il nous faut composer avec les apparences. En définitive, à la condition d'y intégrer les transformations de Lorentz, tout semble se passer selon les lois de Newton, qui sont relatives mais incontournables. Il n'empêche que d'un point de vue absolu (mais inaccessible), tout se passe réellement selon les prévisions de Lorentz. La deuxième loi de Newton en particulier indiquait qu'il faut appliquer une force à la matière pour l'accélérer, la ralentir ou lui faire changer de direction. Sous réserve que les notions d'immobilité, de ralentissement et d'accélération sont désormais hautement subjectives, c'est tout à fait juste. Il faut considérer que Newton avait raison. Par contre, il importe de corriger ses formules pour qu'elles tiennent compte désormais de l'augmentation de la masse, qui lui était inconnue, et qui est d'ailleurs tout aussi subjective.
Il nous faut faire un choix. Nous sommes donc en possession de deux formules dont l'approche est radicalement différente, l'une relative, l'autre absolue, mais qui produisent pourtant les mêmes résultats. C'est très rassurant, mais encore faudrait-il s'entendre sur le référentiel à privilégier et sur les modalités d'application. La Relativité nous indique en effet que deux observateurs dont la vitesse n'est pas la même obtiendront des résultats contradictoires en observant le même phénomène. En fait, de nombreux observateurs obtiendront tout un éventail de résultats inconciliables, et c'est pourquoi il serait souhaitable de mettre en place une convention. Je montre à la page suivante (la dynamique des champs de force) qu'il existe une solution très intéressante fondée sur la présence obligatoire d'un champ de force. Cette méthode permet de concilier les différents résultats à la satisfaction de chacun en recourant à un "arbitre impartial". Elle permet aussi de simplifier les lois et les calculs en éliminant toute référence à la Relativité (même celle de Lorentz) et en revenant fondamentalement à la mécanique de Newton. Soyons réalistes : à peu près personne n'est arrivé à comprendre correctement la Relativité, y compris Einstein lui-même... Nous savons que la mécanique de Newton fonctionne bien si les vitesses sont faibles. Désormais elle fonctionnera tout aussi bien à des vitesses qui frôlent celle de lumière à deux conditions : 1. - Définir un référentiel privilégié. 2. - Tenir compte de l'augmentation de la masse. C'est surtout la compatibilité avec l'attitude actuelle des physiciens qui apparaît importante. Ils répugnent manifestement à tenter d'évaluer comment ils percevraient la situation s'ils chevauchaient un électron qui file dans un accélérateur de particules à une vitesse proche de celle de la lumière. Ils ne sont guère tentés d'invoquer la Relativité d'Einstein pour calculer la trajectoire d'un engin spatial ou la position d'un objet sur terre grâce au système GPS par satellite. Ils préfèrent de loin continuer d'utiliser sensiblement les mêmes lois et les mêmes formules, et j'ai donc toutes les raisons de penser que cette méthode sera peu à peu adoptée par tous en vertu de la loi du moindre effort : « Pourquoi faire compliqué quand on peut faire simple ? » Je cite cette loi et j'en suis désolé, mais il le faut bien. Combien de personnes sur cette planète sont en mesure de calculer correctement le déplacement du périhélie de Mercure à l'aide du calcul tensoriel proposé par Albert Einstein ? Et ne devraient-ils pas tenir compte simultanément de la présence de Jupiter et de Saturne en particulier comparativement à un centre d'inertie qui indique que le Soleil lui-même n'est pas fixe dans cet ensemble ? Et ce serait peine perdue car la complexité des calculs nécessaires selon Einstein ne garantirait pas pour autant des résultats plus précis. Soyons clairs : la gravité est une force comme les autres et elle obéit aux lois de Newton. Les vitesses impliquées sont normalement très inférieures à celle de la lumière et n'existe donc pas de "Relativité Générale". L'un des principes de la dynamique des champs de force indique que Le Verrier a fait l'erreur d'omettre de définir le référentiel privilégié correct. Un calcul plus rigoureux devrait modifier sensiblement les résultats dans le cas de Mercure, sachant que l'anomalie dans le déplacement du périhélie est vraiment minime. Il existe aussi sûrement bien d'autres petites anomalies dont on n'a pas tenu compte. Il ne reste donc qu'à les trouver et à refaire les calculs en conséquence sans devoir recourir à des théories fumeuses et vaporeuses telles qu'une prétendue "courbure de l'espace" qui d'ailleurs n'explique rien du tout. Voyons donc comment mettre à niveau la mécanique de Newton.
Le champ de force. L'énergie résulte d'une force appliquée pendant un certain temps ou sur une certaine distance en tenant compte d'une accélération. Mais d'où vient cette force ? Très certainement, d'un champ de force, dont l'exemple le plus évident est le champ électrostatique.
Le champ électrostatique résulte de la composition des ondes provenant de deux électrons ou positrons. Il s'agit d'ondes stationnaires qui sont ensuite amplifiées par les ondes de l'éther.
Si deux électrons sont en présence, ils subissent une force de répulsion mutuelle, qui est une force positive. Si un électron et un proton (ou un positron) sont en présence, ils subissent plutôt une force d'attraction. J'ai montré à la page sur la force de Coulomb que s'il en est ainsi, c'est parce que les ondes que deux électrons émettent l'un vers l'autre interfèrent et forment des ondes stationnaires très particulières. Depuis ce temps, j'ai également mis au point des programmes que vous pouvez télécharger ci-dessous si ce n'est déjà fait : Je vous suggère fortement d'examiner le code source du programme Ether11.bas, qui montre ces champs de force sous toutes leurs coutures. Tout comme les électrons eux-mêmes, ces ondes stationnaires que sont les champs de force sont amplifiées par les ondes qui circulent dans l'éther. Leur énergie en est accrue d'une manière significative, et cette énergie est sans cesse rayonnée en direction des deux électrons. D'une manière remarquable, ces ondes parviennent constamment en phase à chaque électron peu importe la distance qui les sépare. Cela s'explique par le fait que la vitesse des ondes progressives qui traversent des ondes stationnaires varie selon l'amplitude de celles-ci à la condition qu'elles se propagent dans le même axe. C'est une chose qu'on pourra vérifier facilement en étudiant la vitesse des sons qui se propagent à travers des ondes stationnaires, en particulier dans un médium compressible tel que l'air. À mesure que nos études progressent, il devient évident que chaque onde possède un "personnalité" propre qui dépend largement du médium dans lequel elle se propage. Bref, on a eu tort de penser qu'une onde se résume à une équation. Il s'agit en réalité d'un phénomène mécanique fort complexe, hautement variable selon la situation, et qu'il faudra étudier avec plus d'attention. En plus clair, l'énergie des ondes que deux électrons émettent l'un vers l'autre est négligeable. Au contraire, l'énergie des ondes stationnaires que ces ondes produisent est considérable. Ces ondes stationnaires constituent le champ électrostatique, l'un des nombreux champs de force. Ce champ de force ne contient pas d'électrons. Il est donc invisible et difficile à mettre en évidence, mais il constitue pourtant de la matière à toutes fins pratiques. Il contient de l'énergie, d'ailleurs en quantités énormes si les électrons sont très rapprochés; on obtient alors un champ gluonique. Bien qu'il se situe dans un espace considérable, on peut considérer que son centre d'inertie se trouve au centre de l'axe qui joint les deux électrons. Il ne bouge pas du point de vue d'un observateur qui se situe à cet endroit. C'est normal puisqu'il s'agit également du centre d'inertie. Le principe de la double action. L'effet de répulsion entre électrons est donc la conséquence de la pression de radiation exercée de part et d'autre par le champ électrostatique, qui se situe exactement entre les deux. En toute objectivité, puisqu'on ne peut pas privilégier un électron aux dépens de l'autre en raison de la symétrie, il faut reconnaître ne s'agit pas d'une action suivie d'une réaction. Nous sommes plutôt en présence d'une double action de force égale et de sens opposé. Il arrive fréquemment qu'un champ de force agisse sur deux corps dont la masse n'est pas la même. En particulier, le champ de gravité est "virtuel" et il agit en réalité en exerçant une pression de radiation à partir de deux champs opposés extérieurs. Tout se passe alors quand même comme si un "champ d'attraction" était situé entre ces deux corps, son énergie leur étant distribuée en deux parts égales. Puisqu'il faut moins d'énergie pour accélérer rapidement un corps moins massif, c'est ce dernier qui en est le plus influencé. Mais là encore, il s'agit bel et bien d'une double action puisqu'il est impossible de distinguer l'action de la réaction. Il faut signaler en particulier que l'effet est simultané. Il n'y a donc plus d'objection à ce que les ondes responsables de la gravité se propagent à la vitesse de la lumière. On avait noté depuis longtemps que l'effet de la gravité devrait préférablement être instantané, les ondes traversant chacun des deux corps avant d'agir sur l'autre. Mais cela ne tient plus si la force est exercée par un champ intermédiaire. Il faudra donc modifier la loi de Newton sur l'action et la réaction et la renommer la loi de la double action.
I - La première loi de Newton : le principe d'inertie. Il est clair que le référentiel d'un solide isolé est celui où il semble au repos. On ne voit pas très bien comment un solide isolé pourrait se déplacer en ligne droite et à vitesse constante dans "son" référentiel, comme la loi initiale de Newton le suggère. S'il semble s'y déplacer, ce ne peut être que parce qu'il est observé du point de vue d'un autre référentiel. C'était peut-être acceptable autrefois en vertu du principe de Relativité de Galilée, mais il aurait fallu admettre depuis un siècle qu'il ne peut pas exister de "référentiel galiléen" à cause des transformations de Lorentz. Dans l'absolu, un référentiel ne peut être que cartésien et il doit être au repos comparativement à l'éther. Répétons-le : il ne peut exister qu'un référentiel cartésien véritablement au repos dans l'éther. Toute allusion à un référentiel dit "galiléen" est à proscrire en raison de la distorsion qui y règne. Mais Lorentz et Poincaré ayant découvert que cette notion de repos était invérifiable, il demeure possible en vertu de la loi de la Relativité de parler d'un référentiel privilégié à la condition de présumer malgré tout qu'il est au repos. On considère donc qu'un autre objet qui s'y déplace subit les transformations de Lorentz (c'est à dire l'effet Doppler) en fonction de sa vitesse apparente. Il faut le soumettre aux équations de Lorentz ou encore à mon Scanner du Temps dans le but d'y observer comment la situation semblera y évoluer vue du référentiel privilégié. Bref, on ne peut plus considérer que le centre d'inertie commun de deux ou de plusieurs solides en interaction se déplace en ligne droite et à vitesse constante. Pour en obtenir une analyse correcte, il faut obligatoirement le considérer au repos. Il convient donc de reformuler la première loi de Newton en ce sens. Ce sera le cas par exemple du système solaire, le soleil lui-même s'y déplaçant à cause de la masse non négligeable de Jupiter et de Saturne en particulier. Cela permettra d'élaborer à la page suivante la dynamique des champs de force. Rappelons que le principe d'inertie est une découverte de Galilée, que Newton n'a d'ailleurs jamais revendiquée :
La première loi de Newton sur l'inertie revue et corrigée. Il s'agit en fait d'immobiliser l'observateur pour éviter qu'il ne subisse les transformations de Lorentz.
II - La deuxième loi de Newton : l'application d'une force produit une accélération. On connaît la célèbre formule : f = m * a. Encore une fois, il faudra la corriger à cause de l'augmentation de la masse, mais cela nous obligerait ici à recourir au calcul différentiel puisque la masse augmente progressivement en fonction de l'accélération. Sachant que l'accélération se fait selon la loi de l'addition des vitesses de Poincaré, on peut prévoir que la formule révisée sera complexe. S'il existe plusieurs forces, il faut tenir comte de leurs composantes. De plus, pour une force donnée, l'accélération est moindre si la masse est plus grande. Mais Newton ignorait tout de l'augmentation de la masse et il devient nécessaire de modifier sa deuxième loi en conséquence. Il faut aussi préciser qu'à cause des transformations de Lorentz et de la Relativité, le référentiel de l'observateur doit être présumé au repos pour éviter des résultats contradictoires :
La deuxième loi de Newton revue et corrigée. Les ondes de tout corps qui accélère subissent (ou semblent subir) l'effet Doppler, c'est à dire les transformations de Lorentz. La compression des ondes se traduit par une augmentation de la masse de ce corps. C'est pourquoi il accélérera de moins en moins vite si la force appliquée est constante.
III - La troisième loi de Newton : un champ de force réputé au repos produit deux forces égales en sens opposé. En raison de la loi de la conservation de la masse et de l'énergie, on peut faire remarquer que la masse totale T des deux boules de billards montrées ci-dessous, soit 3 kilogrammes, demeure inchangée avant et après le choc :
Le problème, c'est que le référentiel de ce système correspond au référentiel initial de la boule de billard montrée à droite. Or dès que cette boule accélère, ce référentiel devient étranger à ce système, car il est hautement improbable que l'autre boule s'y immobilise exactement comme c'est le cas ici. Cette situation conduit à des résultats peu concluants puisqu'ils varient selon le référentiel choisi. Il vaut mieux choisir un référentiel dans lequel on pourra observer ce processus en toute stabilité, et ce référentiel ne peut être que celui du centre d'inertie, où se situent l'ensemble des champs de force électrostatiques. On peut alors en toute confiance considérer que c'est lui qui demeure au repos dans son référentiel car cela produit un scénario plus symétrique à "double action" qui ressemble à ceci :
La transposition n'est pas correcte ici puisqu'on a plutôt 4 kilogrammes au total, mais peu importe. On a vu que dans l'absolu, selon Lorentz, l'action et la réaction ne sont pas égales, mais que l'analyse de ce point de vue est impraticable à cause de la Relativité. Pourtant, il existe toujours une situation qui permet de considérer que l'énergie du champ de force est distribuée en deux parts égales et en sens opposé à chacun des deux corps en interaction. C'est ce qui semble se produire si le référentiel correspond à celui du centre d'inertie commun, qu'on peut confondre ici avec celui du champ de force.
La troisième loi de Newton récupérée in extremis. Le principe de l'action et de la réaction devient un principe de double action. Ce principe conduit à la "dynamique des champs de force", qui est traitée à la page suivante.
S'il y a trois corps ou plus, l'effet Doppler affecte les champs de force et le principe de double action ne tient plus puisque l'égalité des forces est compromise. Des forces actives et réactives inégales apparaissent et elles sont proportionnelles à l'effet Doppler avant et arrière. Le calcul ultra-précis du comportement du système solaire serait donc difficile, mais une telle précision n'est généralement pas requise puisqu'on n'a pas affaire à des vitesses "relativistes".
La dynamique des champs de force. Répétons-le : la dynamique de la matière, c'est la dynamique des ondes. Toutefois, pour des raisons de compatibilité et pour des raisons d'ordre pratique évidentes, il vaut mieux adopter plutôt l'expression : la dynamique des champs de force. Il s'agit simplement de reconduire la mécanique de Newton en lui apportant les modifications nécessaires. Selon la théorie de la Relativité, deux observateurs dont la vitesse n'est pas la même se perçoivent exactement de la même manière. Par exemple, ils constatent que c'est toujours "l'autre" qui est contracté. Il faut bien le reconnaître, ce n'est pas un paradoxe : il s'agit purement et simplement d'une contradiction, qui ne peut s'expliquer que si l'un d'eux (probablement les deux, en fait) est victime d'une illusion. Or la présence d'un centre d'inertie commun réputé stable permet de lever cette contradiction. Par convention, on décrète donc que l'observateur doit se situer dans ce référentiel privilégié et que tous les autres observateurs sont victimes d'une illusion à cause de l'effet Doppler et de leur propre transformation. Les lois de Newton revues et corrigées ne sembleront exactes aux yeux de l'observateur que dans ces conditions.
Un référentiel privilégié. D'une part, cet observateur joue le rôle d'un arbitre impartial. Il n'a aucune raison de favoriser un référentiel aux dépens de l'autre. Son référentiel est privilégié car il est unique, ce qui élimine la symétrie caractéristique mais illogique de la Relativité. D'autre part, ce que cet arbitre verra ne correspondra sans doute pas à la vérité absolue : alors il demeure possible d'effectuer la transposition des résultats selon la loi de l'addition des vitesses de Poincaré, ou mieux grâce à mon Scanner du Temps. Il existe tout un éventail de possibilités, mais le point de vue de l'arbitre demeurera compatible avec ce que constateront et calculeront les autres observateurs, pourvu qu'ils se mettent d'accord sur cette procédure. Lors d'un processus apparent d'action et de réaction, on peut donc considérer qu'un champ de force exerce plutôt deux forces en sens opposé parfaitement égales conformément à la troisième loi de Newton révisée (le principe de double action) à la condition de les évaluer d'abord dans le référentiel du centre d'inertie des corps impliqués. Mais avant d'aller plus loin, il faut souligner que dans les faits, l'action et la réaction ne semblent pratiquement jamais simultanées ni symétriques. Cette absence apparente de symétrie sera normalement observée comme une cause suivie d'un effet, d'où le principe de Causalité.
Le principe de Causalité. Il est vrai que tout effet a une cause, mais il convient de préciser que cet effet est un mouvement et que cette cause est une onde qui se propage dans l'éther à la vitesse de la lumière. Le mouvement n'est rien d'autre qu'une modification par effet Doppler des ondes que la matière contient. On savait qu'un cause produit un effet, mais il devient clair que les effets produisent de nouvelles causes dans une réaction en chaîne sans fin qui est fortement assujettie à la vitesse de la lumière. On a successivement un mouvement, un rayonnement, un champ de force, une pression de radiation et enfin, un nouveau mouvement. Toute la splendeur de notre univers se résume à un déplacement d'électrons qui subissent l'effet Doppler et qui s'influencent mutuellement grâce aux ondes qu'ils reçoivent et qu'ils émettent. Je propose donc cette formulation du principe de Causalité :
Le principe de Causalité.
J'ai du mal à me convaincre que "les mêmes causes produisent les mêmes effets" parce que cette énoncé conduit au déterminisme, qui est une hypothèse aussi plausible qu'invérifiable. Cela revient à dire que l'avenir est la somme de toutes les causes et qu'il est inexorable. Pour court-circuiter ce déterminisme, il faudrait que le hasard y retrouve ses droits. On constate en effet que les statistiques se vérifient, ce qui suggère fortement que le hasard agit bien comme on le suppose. Mais on ne voit pas très bien comment, d'un point de vue mécanique, il pourrait opérer. En pratique, il n'arrive jamais que deux causes soient parfaitement identiques. Elles ne peuvent donc jamais produire les mêmes effets. Hélas ! cela ne fait qu'amplifier notre illusion que nous jouissons d'une liberté, qui nous apparaît pourtant si naturelle. De plus, nos ordinateurs deviennent de plus en plus puissants et nous pouvons prédire de mieux en mieux le temps qu'il fera demain. S'il en est ainsi, peut-être pourrons-nous prédire un jour assez exactement de quoi demain sera fait, et alors notre liberté en prendra pour son rhume... Certains en arriveront à la conclusion que nous sommes les passagers d'un train dont les rails déjà en place conduisent fatalement à une destination fixée à l'avance, et qu'il est impossible d'éviter ou de modifier. Selon eux, nous ne pouvons que découvrir le paysage à travers la fenêtre à mesure qu'il apparaît. Mais d'autres refuseront même d'envisager cette hypothèse. Nous n'aurons sans doute jamais de réponse à cette question et d'ailleurs, l'ultime question serait plutôt celle-ci : quelle fut la Cause de l'éther ?
La vitesse de la lumière est constante et déterminante. Le rayonnement se transmet par les ondes de l'éther à la vitesse de la lumière. Sachant que leur énergie décroît selon le carré de la distance, on conçoit qu'un même rayonnement n'agit pas simultanément ni avec la même force en différents endroits. Mais surtout, à cause des transformations de Lorentz, tout se passe d'une manière très différente dans un système qui se déplace à travers l'éther. Toute force y agit même selon des heures locales. Parce que la vitesse de la lumière se mesure comparativement à l'éther, les forces s'y transmettent à une vitesse relative inférieure à celle de la lumière, et comme Michelson l'a montré, cette vitesse sur un aller et retour est encore plus lente sur l'axe du déplacement. Toute la mécanique de la matière s'en trouve ralentie et même les distances sur l'axe se contractent. Bref, dès qu'on suppose que la matière est faite d'ondes et qu'elle fonctionne à l'aide d'ondes, on trouve que les transformations de Lorentz expliquent merveilleusement la Relativité. Celle de Lorentz, bien entendu. Et enfin, on a vu que les lois de Newton sont finalement beaucoup plus assujetties à la vitesse de la lumière que ce dernier ne l'avait envisagé. C'est très clair : la grandeur c au carré y est omniprésente. Tout cela n'est possible que si la vitesse de la lumière est constante comparativement à l'éther. On peut montrer que les ondes qui circulent dans l'éther doit ralentir ou accélérer très faiblement si elles traversent des ondes stationnaires. C'est ce qui assure le fonctionnement des électrons et des champs de force. Mais si cette vitesse devait varier d'une manière significative, le comportement de la matière deviendrait chaotique et elle ne pourrait tout simplement plus exister.
La gravité ne courbe pas l'espace. Le champ de gravité se manifeste apparemment par un seul champ de force situé au centre d'inertie commun à deux corps, et qui exerce une force d'attraction. En réalité, il s'agit à la fois d'un champ de force central et de deux autres champs de force opposés et extérieurs aux deux corps. La page sur la gravité a été révisée il y a longtemps en ce sens. Elle montre comment ces champs de force se forment à partir des ondes émises par la matière d'une part, et d'autre part à partir des ondes planes qui circulent dans l'éther. Il faut considérer que les ondes qui ont traversé la matière ont contribué à son amplification. Elles en sont affaiblies et l'énergie correspondante se retrouve dans les ondes sphériques que la matière rayonne en permanence, et qui sont incapables d'exercer une pression de radiation identique. En effet, un champ de force est toujours fait principalement d'ondes stationnaires axiales, dont le diamètre est réduit si l'un des deux trains d'ondes qui l'a formé est fait d'ondes sphériques. C'est vrai à plus forte raison si les deux trains d'ondes sont faits d'ondes sphériques. La dynamique de la gravité étant attribuable à des champs de force, elle peut être évaluée grâce à la dynamique des champs de force traitée à la page suivante. Il faut souligner que cette méthode permet de contourner sans peine la Relativité et de revenir à la formule de Newton sur la gravité à la condition de tenir compte de l'augmentation de la masse et d'un référentiel privilégié. Ainsi donc, la gravité ne courbe pas l'espace. Cette idée est absurde.
La mécanique de Newton peut maintenant affronter l'éternité. Puisqu'on parle d'ondes et de mouvement, il est clair qu'il faut tenir compte de l'effet Doppler. C'est même le point essentiel : les formules qui permettent d'expliquer concrètement et complètement la dynamique de la matière font appel uniquement à l'effet Doppler. On sait que selon les transformations de Lorentz, tous les phénomènes y compris la fréquence des électrons qui composent la boule de billard mobile se déroulent plus lentement. Pour reprendre l'exemple utilisé plus haut, la fréquence d'origine F est donc ralentie selon le facteur g : F ' = g F = 0,5 F De plus, l'effet Doppler en fréquence vers l'avant vaut : Fa = F ' / (1 – bêta) = 0,5 / (1 – 0,866) = 3,732 F Les indices a et r font référence à l'action et à la réaction, et donc ici aux ondes circulant vers l'avant ou l'arrière. Malgré le ralentissement de la fréquence des électrons, la fréquence des ondes qu'ils émettent vers l'avant augmente quand même. C'est donc aussi le cas de leur énergie, qui sera responsable de la force que ces ondes exercent. En effet, l'énergie des ondes étant proportionnelle à leur fréquence, on est en présence d'une énergie "active" dirigée vers l'avant et valant 3,732 fois celle des électrons au repos. Rappelons que contrairement à l'effet Doppler normal, cet effet Doppler "relativiste" est parfaitement symétrique. En effet, la fréquence des ondes qui se dirigent vers l'arrière vaut plutôt : Fr = F ' / (1 + bêta) = 0,5 / (1 + 0,866) = 0,26795 F Ici, contrairement à l'effet Doppler normal, l'une des fréquences est exactement l'inverse de l'autre. C'est à cause de cette réciprocité diabolique que la symétrie caractéristique de la Relativité de Lorentz se vérifie : Fa * Fr = 1 1 / Fa = Fr 1 / 3,732 = 0,26795
Répétons-le, l'énergie cinétique n'est que la conséquence de la compression des ondes par effet Doppler. Dès qu'on le réalise, la mécanique de Newton devient du coup beaucoup plus logique et limpide. Pour faire autorité, cette page aurait bien besoin d'être entièrement refaite par des physiciens dont ce serait la spécialité. Il n'empêche que ses bases ne sont plus discutables, car elle permet non seulement de prévoir les phénomènes avec une précision inégalée à ce jour, mais aussi de les comprendre. Il faut bien le dire : Einstein n'a jamais pu expliquer pourquoi la matière se comporte ainsi. Et fort heureusement, même revue et corrigée, la mécanique de Newton demeure relativement simple. Pour bien comprendre la matière, il suffisait de bien connaître l'effet Doppler selon Lorentz. |
| 01 | 02 | 03 | 04 | 05 | 06 | 07 | 08 | 09 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| Vous êtes ici | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 |
Gabriel LaFrenière, Bois-des-Filion en Québec. Sur l'Internet depuis septembre 2002. Dernière mise à jour le 12 septembre 2009. Courrier électronique : veuillez consulter cet avis. La matière est faite d'ondes, © Gabriel Lafrenière, juin 2002. |
ANTONIVS·MORO·BRVTVS·EST