L'EFFET DOPPLER

L'effet Doppler explique tout.
Téléchargez cette vidéo, qui montre le phénomène dans toute sa splendeur :
|
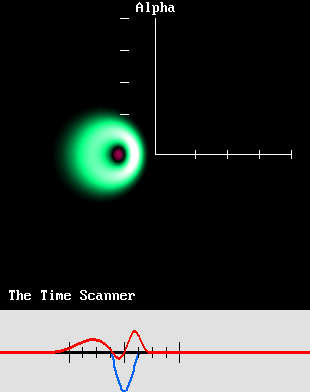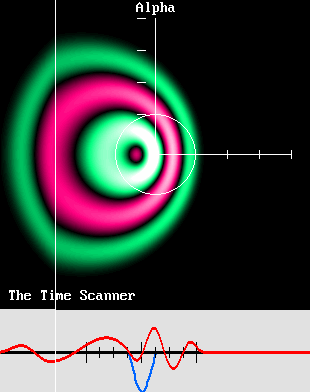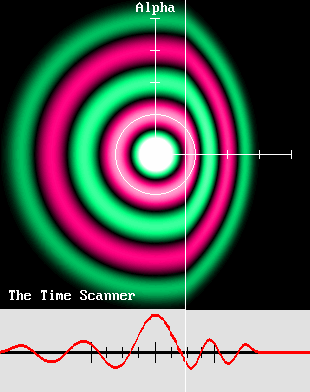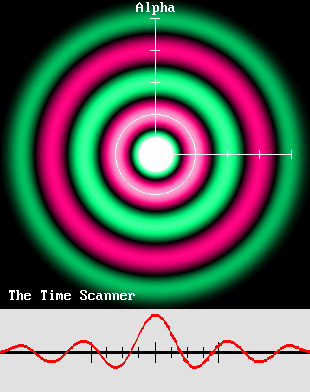
Les images proposées ci-dessus ont ceci de remarquable qu'elles correspondent aux transformations de Lorentz. Pour les réaliser, il a fallu faire intervenir les équations de Lorentz, mais en les inversant. Il a aussi fallu recourir au médium virtuel créé par M Philippe Delmotte et simplifié par M. Jocelyn Marcotte, et qui constitue désormais un outil incontournable pour étudier les ondes. Il a encore fallu mettre en œuvre mon Scanner du Temps. De plus, j'ai réussi à représenter les deux transformations réciproques mises en avant par Henri Poincaré dans la même opération. Et enfin, grâce à ma plus récente découverte, la vitesse Alpha, j'ai pu démontrer que les transformations de Lorentz n'impliquent pas nécessairement une modification des mesures du temps et de l'espace. En effet, l'échelle des longueurs d'onde montrée ci-dessus n'est jamais modifiée. Elle peut donc servir de référence absolue. Tout ceci démontre que la version de la Relativité qui a été proposée par Lorentz en 1904 était tout à fait juste. L'effet Doppler explique le mouvement, l'énergie et la mécanique de la matière. L'effet Doppler explique les effets électromagnétiques. L'effet Doppler explique les lois de Newton, par exemple l'action et la réaction. L'effet Doppler explique l'augmentation de la masse pressentie par Lorentz. L'effet Doppler explique les transformations de Lorentz et la Relativité. Si comme moi vous adorez la physique, ces images devraient vous séduire et vous enchanter. Elles méritent qu'on les analyse, qu'on les explique et qu'on les comprenne. C'est la voie de l'avenir. Il faut sortir la physique de l'ornière dans laquelle elle s'est embourbée depuis un siècle. Les conventions. Avant toute chose, il est essentiel de considérer que : – Les ondes ont besoin d'un médium pour se propager. – S'il n'y a pas de médium, il n'y a pas d'effet Doppler. – La vitesse des ondes, de l'émetteur ou du récepteur doit s'évaluer comparativement au médium. – L'expression "au repos" signifie au repos comparativement au médium. – Le Principe de Relativité de Galilée est inapplicable en présence d'un tel médium. Un mouvement ne peut pas être relatif. Il est absolu et il ne peut se faire que comparativement à un point au repos. En conséquence, au lieu d'un référentiel galiléen, on parlera d'un référentiel cartésien qui sera réputé au repos, et dont les coordonnées x, y et z seront euclidiennes. La vitesse normalisée bêta. Henri Poincaré posait : c = 1 dans le cas de la vitesse de la lumière, ce qui lui permettait de supprimer cette grandeur et même son carré dans ses équations. Elles en étaient considérablement simplifiées. Dans ce système, la vitesse d'entraînement de l'émetteur ou du récepteur doit ainsi être comparée à c et donc à 1, de telle sorte que la vitesse normalisée qu'on a représentée par la lettre grecque bêta vaut tout simplement : v / c. Ici, la vitesse c sera celle de n'importe quelle onde, peu importe le médium considéré. Le facteur de contraction de Lorentz. On voit ci-dessous que le facteur de contraction g de Lorentz vaut : g = racine(1 – bêta ^ 2). Il s'agit d'une grandeur incontournable que Poincare appelait "l'aberration". Le facteur gamma de la Relativité vaut l'inverse : gamma = 1 / g.
Cette aberration aurait été découverte par A. A. Michelson. Considérons par exemple un avion dont la vitesse constante vaut la moitié de celle du son dans l'air, donc avec bêta = 0,5. S'il vole en présence d'un fort vent, on peut s'attendre à ce que sa course en soit sévèrement modifiée. Michelson a compris que, l'éther étant le médium responsable de la propagation de la lumière, il devenait possible grâce à cet effet de détecter notre mouvement absolu à travers l'éther. Les avions n'existant pas vers 1887, Michelson avait plutôt imaginé des nageurs en présence d'un fort courant. C'est ce qui l'a conduit à imaginer son interféromètre. Toutefois, Michelson ignorait que son appareil devait se contracter selon le facteur de contraction g de Lorentz, de telle sorte qu'il était en définitive incapable de révéler le mouvement absolu de la terre. |
1 – L'EFFET DOPPLER NORMAL.
(L'émetteur se déplace et l'observateur est au repos).
Il faut considérer le point d'origine du front d'onde et non la plus récente position de l'émetteur.
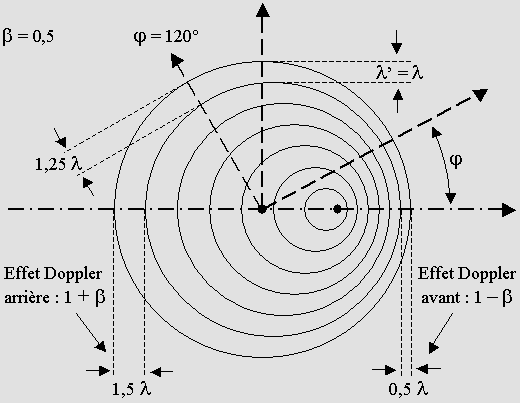
L'effet Doppler normal.

|
Supposons que bêta vaut 0,5 et voyons comment l'effet Doppler modifie les ondes : 1. La longueur d'onde vers l'avant est : 1 – bêta = 0,5 fois plus courte. 2. La longueur d'onde vers l'arrière est : 1 + bêta = 1,5 fois plus longue. 3. La fréquence vers l'avant est : 1 / (1 – bêta) = 2 fois plus élevée. 4. La fréquence vers l'arrière est : 1 / (1 + bêta) = 0,6667 fois plus basse. 5. La longueur d'onde pour un angle phi = 120° est : 1 – bêta * cos 120° = 1,25 fois plus longue. 6. La fréquence pour un angle phi = 120° est : 1 / (1 – bêta * cos 120°) = 0,8 fois plus basse. 7. La fréquence et la longueur d'onde demeurent inchangées sur un plan orthogonal (90°) comprenant l'origine de l'onde. 9. On peut retrouver la vitesse bêta d'après la contraction de la longueur d'onde vers l'avant : bêta = 1 – 0,5 = 0,5. 10. On peut retrouver la vitesse bêta d'après la dilatation de la longueur d'onde vers l'arrière : bêta = 1,5 – 1 = 0,5. 11. Le rapport des longueurs d'onde avant et arrière vaut : R = (1 + bêta) / (1 – bêta) = 3 12. On peut retrouver la vitesse bêta d'après ce rapport : (3 – 1) / (3 + 1) = 0,5 13. Exceptionnellement, le facteur de contraction g de Lorentz n'est d'aucune utilité ici.
L'observateur peut utiliser un résonateur ou un dispositif plus sophistiqué pour mesurer la fréquence. On sait qu'un réflecteur plan permet de produire des ondes stationnaires, ce qui permet de mesurer la distance du premier nœud : c'est le test de Hertz. Dans tous les cas, l'observateur relève des mesures exactes parce qu'il est au repos. Il doit néanmoins interpréter ces résultats. Par exemple, Mars et Jupiter, s'ils apparaissent sur la même photographie, n'ont jamais été en réalité dans cette position parce que la lumière met beaucoup plus de temps à parvenir de Jupiter. De la même manière, il arrive que l'effet Doppler doive être interprété avec soin, surtout si l'observateur lui-même est en mouvement. L'effet Doppler produit parfois des effets qui ne sont pas bien compris, ce qui explique que la Relativité est si déroutante. Beaucoup ne prennent pas la peine de bien analyser ce qui se passe. Avouons-le, c'est de la paresse, et c'est une honte car le calcul est toujours d'une simplicité désarmante. On n'a jamais besoin de recourir à des équations complexes. Les transformations de Voigt. Croyez-le ou non, l'effet Doppler normal dont il est question ici peut être reproduit (ou corrigé) à l'aide des équations de Woldemar Voigt (1887), que Lorentz a empruntées pour établir ses propres transformations. En fait, elles peuvent également reproduire les transformations de Lorentz car dans ce cas il suffit de supprimer la constante de Voigt. Henri Poincaré utilisait encore la version de Voigt en 1905 comme en fait foi cette transposition de son texte en notation moderne, réalisée par M. Christian Marchal :
Les transformations de Lorentz selon Poincaré. Elles présentent encore la constante de Voigt l (k ci-dessous), qui fut supprimée par Lorentz après l'avoir trouvée égale à 1.
J'ai réussi à corriger et à inverser les équations de Voigt, dont la constante k permet de varier la fréquence : x' = x * g * k + t * bêta t' = t * g / k – x * bêta y' = y * k z' = z * k Toutefois, puisque la constante k est égale au facteur g de Lorenz dans le cas de l'effet Doppler normal, on peut simplifier : x' = x * g ^ 2 + t * bêta t' = t – x * bêta y' = y * g z' = z * g
Ces équations produisent un effet Doppler tout à fait normal. Ce n'est pas une blague ! Elles fonctionnent même magnifiquement, et je suis donc surpris qu'elles soient toujours ignorées. Je rappelle que les variables x et x' représentent la longueur d'onde et non l'espace. De même, les variables t et t' représentent la période des ondes (t = 1 signifiant 2 * pi radians) et non pas le temps. Ces équations ont même pour effet de déplacer l'émetteur (t * bêta indique un mouvement de translation), comme ce programme le démontre : Doppler_Voigt_transformations.bas Doppler_Voigt_transformations.exe |
2 – L'EFFET DOPPLER VIRTUEL.
(L'émetteur est au repos; c'est plutôt l'observateur qui se déplace.)
|
Dans ce cas, il ne se produit pas d'effet Doppler véritable. La fréquence et la longueur d'onde demeurent inchangées. L'observateur expérimenté sait bien que ses instruments se déplacent et qu'ils ne peuvent plus les enregistrer correctement puisque la cadence de réception en est modifiée. Si l'observateur s'éloigne de la source, la cadence de réception (et non la fréquence des ondes, f ' étant donc inexact) ralentit. Elle augmente au contraire s'il se rapproche. Cet effet Doppler apparent, virtuel, se calcule de la manière suivante : L'observateur va à la rencontre de la source : f ' = f (1 + bêta) L'observateur s'éloigne de la source: f ' = f (1 – bêta) La trajectoire de l'observateur fait un angle "phi" comparativement à la source : f ' = f (1 – bêta cos phi)
Supposons encore que bêta vaut 0,5 et voyons comment l'effet Doppler virtuel semble modifier la fréquence, qui dans les faits demeure inchangée. 1. Si l'observateur se dirige vers la source, la fréquence semble être : 1 + bêta = 1,5 fois plus élevée. 2. Si l'observateur s'éloigne de la source, la fréquence semble être : 1 – bêta = 0,5 fois plus basse. 3. Pour tout autre angle, disons 120°, la fréquence semble modifiée selon : 1 – bêta cos 120° = 1,25 fois la fréquence réelle. Bien évidemment, la longueur d'onde demeure inchangée. Par contre, le test de Hertz effectué dans ces conditions produit une contraction ou une dilatation, réelle cette fois-ci, de la longueur de l'onde réfléchie. Alors la distance du premier nœud en est modifiée, ce qui fausse les lectures de l'observateur. On obtient dans ce cas des ondes stationnaires mobiles, qui on l'a vu dans une page précédente présentent une contraction (ou une dilatation) apparentée au facteur g de Lorentz. L'observateur doit donc être parfaitement informé de ce phénomène s'il veut tout de même mesurer la longueur d'onde d'origine à l'aide du test de Hertz. On verra qu'il doit se montrer encore plus prudent en présence de l'effet Doppler "relatif" ci-dessous. Mais un tel calcul devient impossible dans le cas de l'effet Doppler "relativiste" (l'effet Doppler selon Lorentz) à cause de la compression (selon le facteur g) du dispositif mécanique utilisé pour mesurer la longueur des ondes. Cette compression se faisant uniquement dans le sens du déplacement, il devient impossible de relever la différence comparativement à un trajet orthogonal. L'interféromètre de Michelson n'est plus d'aucune utilité pour cette raison. |
3 – L'EFFET DOPPLER RELATIF (et non pas relativiste)
L'émetteur et l'observateur se déplacent ensemble à la même vitesse.
L'axe transversal se déplace avec la source, par exemple une source sonore.
La lumière et les ondes radio sont exclues : leur comportement est toujours Lorentzien (relativiste), jamais relatif.
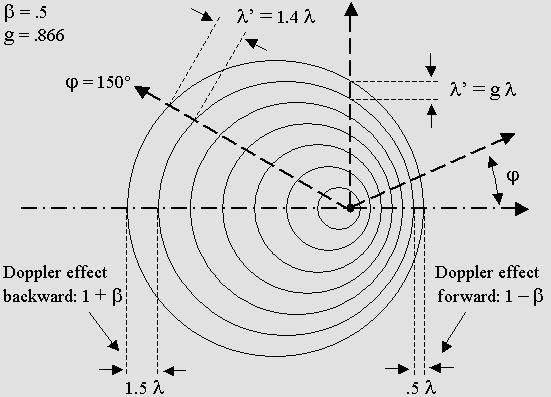
Sur l'axe du déplacement, l'effet Doppler relatif est identique à l'effet Doppler normal.
La formule tous azimuts étant introuvable, j'ai dû l'élaborer moi-même vers 1998.
J'ai finalement trouvé sur le site de M. Ivanov la deuxième formule, qui fonctionne tout aussi bien:
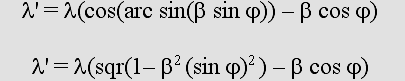
Il faut observer que sur l'axe transversal y, les ondes sont inclinées selon une angle thêta = arc sin bêta.
De plus, ces ondes, tout comme les ondes stationnaires transversales, se contractent selon le facteur g de Lorentz.
Sur l'axe du déplacement x, les ondes stationnaires se contractent encore davantage, soit selon g 2.
| Je souligne que cette contraction inégale des ondes stationnaires sur les axes x et y est d'une importance capitale. |
|
Il faut insister sur le fait que, dans ce système en mouvement, la longueur d'onde d'un son telle que mesurée par l'observateur ne correspond absolument pas à sa longueur d'onde réelle. Bien sûr, puisque l'émetteur se déplace, le son est bel et bien affecté de l'effet Doppler. Mais étonnamment, l'observateur n'enregistre aucune variation dans la fréquence peu importe l'angle de réception et celle-ci correspond bel et bien à la fréquence d'émission réelle. Cet effet surprenant a été découvert par Christian Doppler lui-même en 1842 (cent ans avant ma naissance !) et l'équation qui en rend compte cumule l'effet Doppler réel et l'effet Doppler virtuel. Finalement on obtient ceci : f '' = f (1 – bêta cos phi) / (1 – bêta cos phi) ...et donc : f '' = f.
Johann Christian Doppler (1803-1853)
Il faut donc retenir que même si la longueur d'onde n'est pas la même dans les deux sens à cause du mouvement du réflecteur, le test de Hertz révèle malgré tout la présence d'ondes stationnaires mobiles. Les ventres et les nœuds se déplacent à la vitesse du système, ce qui fait qu'ils semblent immobiles aux yeux de l'observateur qui se déplace lui aussi. Le point important, c'est que ces ventres et ces nœuds mobiles se contractent selon le carré du facteur de contraction de Lorentz sur l'axe du déplacement. Ils ne se contractent que selon le facteur g sur un axe transversal. Il est navrant de constater que Michelson n'était pas informé que cette contraction devait se produire, car c'était un scientifique brillant. Même Lorentz et Poincaré ne parlent jamais de la contraction des ondes stationnaires, et il faudra attendre l'étude de M. Ivanov pour rectifier le tir. Voyez plutôt :
Ci-dessus, les ondes stationnaires normales.
Ci-dessus, les ondes "stationnaires mobiles". Observer le déplacement des ventres et des noeuds. Sans ralentissement de la fréquence, la contraction se fait selon g 2. Mais dans le cas de la lumière, la fréquence diminuant selon g d'après Lorentz, la contraction se fait aussi selon g.
Ci-dessus, les ondes redeviennent (apparemment) stationnaires si l'observateur se déplace avec elles.
Pour autant que je sache, ces ondes "stationnaires mobiles" ont été découvertes par M. Yuri Ivanov. Il les a appelées "lively standing waves", c'est à dire des ondes stationnaires animées. Il a aussi noté que la contraction se fait seulement selon le facteur g sur un axe transversal. Mieux encore, il s'est servi de cette démonstration pour affirmer que la matière se contracte de la même manière puisqu'elle est faite d'ondes stationnaires. Je considère donc que M. Ivanov a ainsi réalisé deux pas de géant en physique et qu'il devrait en être immortalisé.Malheureusement, les "transformations d'Ivanov" qu'il propose ne tiennent pas compte du ralentissement de la fréquence déjà découverte depuis longtemps par Lorentz. La contraction de la matière selon g au carré qui en résulte est donc beaucoup trop sévère. Encore pire, son site parle de "rythmodynamics", d'un effet d'araignée et de lévitation. Je n'y crois pas du tout, bien sûr. J'ai tout de même les deux pieds sur terre, même si parfois ça ne se voit pas ! |
4 – L'EFFET DOPPLER SELON LORENTZ
(aussi appelé "relativiste")
La fréquence de l'émetteur, et particulièrement celle de l'électron, ralentit selon le facteur g.
Cet effet Doppler s'applique à la lumière et aux ondes radio, dans tous les cas sans aucune exception.
|
Cet effet Doppler "relativiste" très particulier est bien connu mais de toute évidence, il demeure mal compris et mal interprété. Il faut d'abord et avant tout le renommer. Non seulement Lorentz mérite qu'on le nomme d'après lui, mais cet attribut "relativiste" ne convient absolument pas puisque l'effet Doppler dont il est question est absolu. L'électron se comporte en effet réellement de cette manière, selon sa vitesse absolue à travers l'éther. Il est vrai que cela conduit tout droit à la Relativité, mais celle-ci n'est que le résultat d'une mystification. Les équations qui en rendent compte sont également bien connues :
L'effet Doppler selon Lorentz, tous azimuts.
La contraction des ondes sur l'axe du déplacement, vers l'avant.
La dilatation des ondes sur l'axe du déplacement, vers l'arrière.
Il faut insister sur le fait que si les ondes sont modifiées de cette manière, c'est uniquement parce que la fréquence de l'électron ralentit selon le facteur g de Lorentz. Je me permets donc de vous présenter (prétentieusement !) la "formule du siècle" : |
|
f ' = g f |
La fréquence de l'électron ralentit selon le facteur g de Lorentz.
Il en résulte un effet Doppler très particulier qui se caractérise par une annulation de la contraction des ondes sur les axes y et z.
De cette manière, la matière dont la structure dépend de l'électron ne se contracte pas sur ces axes.
Sur l'axe du déplacement, la matière se contracte selon le facteur g simple et non pas selon g 2.
De cette manière, l'observateur devient incapable de mettre en évidence sa vitesse absolue à travers l'éther.
Si la Relativité se vérifie, c'est uniquement pour cette raison.
|
Ainsi donc, Lorentz a découvert que la matière se contracte selon "l'aberration", c'est à dire le facteur g, avec pour conséquence que la contraction transversale est annulée. Rappelons que Lorentz était fermement convaincu de l'existence de l'éther (il précisait : "l'éther reste sur place") et que les ondes de la lumière devaient aussi se comporter de cette manière. C'est pourquoi il avait recours aux équations de Maxwell pour démontrer son hypothèse, tout comme Poincaré d'ailleurs. L'absence de contraction sur les axes y et z est la toute première condition nécessaire pour que la Relativité se vérifie : y' = y z' = z Les transformations de Lorentz ont aussi pour effet de rendre l'effet Doppler parfaitement symétrique vers l'avant et vers l'arrière, de telle sorte qu'il devient impossible de détecter le mouvement absolu d'un émetteur, par exemple celui d'une galaxie lointaine dont les astronomes évalueraient la vitesse d'éloignement à la moitié de la vitesse de la lumière. En effet, cette vitesse qu'ils lui donnent est totalement arbitraire. Dans les faits, il s'agit tout juste de son mouvement relatif comparativement à nous, à un point tel que cette galaxie pourrait tout aussi bien être parfaitement au repos dans l'éther. En supposant que l'effet Doppler soit normal, c'est à dire sans ralentissement de la fréquence, La longueur d'onde vers l'avant est : 1 – bêta = 0,5 fois plus courte. La longueur d'onde vers l'arrière est : 1 + bêta = 1,5 fois plus longue. Mais si par surcroît, la fréquence de l'émetteur ralentit selon le facteur g de Lorentz, on obtient un effet Doppler surprenant dont la symétrie ne permet plus de détecter le mouvement absolu. La longueur d'onde vers l'avant est : (1 – bêta) / g = 0,577 fois plus courte. La longueur d'onde vers l'arrière est : (1 + bêta) / g = 1,732 fois plus longue. On constate effectivement que la contraction des ondes vers l'avant vaut l'inverse de leur dilatation vers l'arrière : 0,577 = 1 / 1,732 0,577 * 1,732 = 1 C'est l'une des caractéristiques remarquables des transformations de Lorentz, qui pour citer Poincaré "sembleraient un véritable coup de pouce donné par la nature pour éviter que le mouvement absolu de la terre puisse être révélé par les phénomènes optiques." Une telle symétrie s'avère la conséquence la plus inattendue, la plus incroyable de ces transformations. On verra que cet effet Doppler très particulier se traduit par une contraction, un ralentissement des horloges et, pour enfoncer le clou, un décalage horaire. En définitive, la symétrie du phénomène dans son ensemble est d'une perfection inouïe. Elle fait en sorte que chacun a droit à son opinion. Du point de vue de n'importe quel observateur, si quelque chose bouge, ce ne peut être que comparativement à lui. Si donc il voit toutes les galaxies s'éloigner autour de lui, la progression n'étant pas linéaire, cela semble indiquer qu'un hypothétique Big Bang a eu lieu exactement là où il se situe. Il s'imagine au centre de l'univers et personne ne peut démontrer qu'il a tort. Tout cela est terriblement astucieux, magique, grandiose, pour ne pas dire surnaturel, mais en contrepartie l'humanité ne saura peut-être jamais d'où elle vient, ni où elle va... Si on compare avec l'effet Doppler normal, par exemple celui du son produit par un haut-parleur qui vibre sur 1000 Hz et qui se déplace à 60% de la vitesse du son, il n'existe pas de symétrie avant et arrière : L'effet Doppler normal vers l'avant, en fréquence : 1000 / (1 – 0,6) = 2500 Hz L'effet Doppler normal vers l'arrière, en fréquence : 1000 / (1 + 0,6) = 625 Hz Une symétrie parfaite. Par contre, une antenne radio émettant sur 1000 MHz émettra plutôt sur 800 MHz si elle se déplace à 60% de la vitesse de la lumière, soit selon le facteur g = racine(1 – 0,6 ^ 2) = 0,8. Il en résultera un effet Doppler avant et arrière parfaitement symétrique : L'effet Doppler selon Lorentz, vers l'avant : 0,8 * 1000 / (1 – 0,6) = 2000 MHz L'effet Doppler selon Lorentz, vers l'arrière : 0,8 * 1000 / (1 + 0,6) = 500 MHz Si l'on compare ces résultats avec ceux d'une antenne au repos, la fréquence est doublée vers l'avant et elle est réduite de moitié vers l'arrière. On constate que le rapport des fréquences ou des longueurs d'onde est de deux (2) dans les deux cas à la seule condition de convenir que ce rapport doit être supérieur à 1 pour en arriver à une constante : R > 1.
Cette dernière équation permet donc de déterminer la vitesse d'une galaxie peu importe si cette galaxie s'éloigne ou se rapproche (quoiqu'il se produise presque toujours un "redshift"). C'est aussi ce qui explique qu'on puisse détecter un rapport supérieur à 2 dans le cas des galaxies les plus rapides. En effet, puisque rien ne peut atteindre la vitesse de la lumière, ce rapport ne pourrait être supérieur à 2 dans le cas de l'effet Doppler normal. Au contraire, si l'astronome relève un rapport de 10, cela lui indique que la vitesse de la galaxie atteint tout juste 98% de la vitesse de la lumière. Un rapport R de 100 indique 99,98% de la vitesse de la lumière, et ainsi de suite sans jamais l'atteindre. Pourtant, ce calcul ne serait correct que si notre propre galaxie était parfaitement au repos dans l'éther, ce qui est virtuellement impossible. For heureusement, la loi de la Relativité nous autorise à considérer par convention que le référentiel de la terre est privilégié et qu'il est au repos. Si la terre était en mesure d'imposer cette convention à tout l'univers, tous pourraient s'y référer d'une manière absolue. À cause des transformations de Lorentz, il faudrait aussi que les astronomes conviennent que ces galaxies lointaines sont de plus en plus contractées à mesure qu'elles s'éloignent. Une vitesse de 99,98% de la vitesse de la lumière suppose que la galaxie est aplatie à 2% seulement de sa taille originale. Le résultat évident, c'est qu'il doit exister une sorte de "mur du temps" qui s'accorde assez mal avec la constante de Hubble et qui fait en sorte que notre univers est forcément fini et non pas infini. Cette façon de voir les choses permet également de reculer le moment du Big-Bang à des milliards de milliards d'années. Les transformations de Lorentz ne sont rien d'autre qu'un effet Doppler. C'est une évidence si l'on considère que Lorentz avait emprunté ses équations à Woldemar Voigt, qui les avait élaborées en 1887 précisément dans ce but. Il désirait plus exactement annuler l'effet Doppler obtenu à l'aide des équations de Maxwell. Cela signifie qu'il faut inverser les équations Voigt-Lorentz si l'on désire produire un effet Doppler et non pas l'annuler :
Les équations de Lorentz inversées. La réciprocité. De son propre aveu, Lorentz n'a pas vu que ses équations pouvaient être établies de manière symétrique sans en changer la forme, mais uniquement en échangeant les variables et en inversant le signe. C'est Poincaré qui a réussi ce prodige. Et puisque j'ai dû modifier les équations de Poincaré de manière à provoquer un effet Doppler plutôt que de l'annuler, j'ai obtenu finalement un groupe complet qui est beaucoup plus conforme à la vision de Lorentz, qui croyait à la contraction absolue de la matière :
Le groupe complet des transformations de Lorentz, revu et corrigé. Qu'on ne s'y trompe pas, ces équations produisent des résultats différents. En particulier, les variables x et x' s'appliquent au même référentiel cartésien réputé au repos dans l'éther. Toutefois, les grandeurs obtenues correspondent bel et bien à ce que Lorentz, Poincaré et Einstein ont tous proposé. En effet, même Albert Einstein prévoyait qu'un objet mobile devrait nous apparaître plus court, soit selon g x ci-dessus. Il devrait aussi sembler se déplacer conformément à : + bêta * t. Et enfin, tous s'entendent également pour affirmer que le "temps" ralentit selon : g * t. On peut donc s'étonner que personne depuis un siècle n'ait proposé ces formules...
Le programme Ether17.exe (code source : Ether17.bas) reproduit l'effet Doppler selon Lorentz uniquement à l'aide de ces équations inversées. Il s'agit là d'une démonstration sans faille et spectaculaire que Lorentz disait vrai : le "temps" de l'électron ralentit, mais cela signifie en réalité que c'est sa fréquence qui ralentit, Lorentz ayant tout juste pressenti que l'électron présentait des propriétés ondulatoires. Le programme ci-dessous est encore plus instructif car il utilise plutôt les équations de Voigt, que j'ai inversées (et corrigées) de la même manière. L'avantage, c'est qu'on peut vérifier (grâce à un choix de quatre constantes) que la contraction des ondes n'a plus lieu sur l'axe transversal si cette constante "k" est égale à 1 (c'est précisément la découverte de Lorentz) : Doppler_Voigt_transformations.bas Doppler_Voigt_transformations.exe La contraction de la matière. Il est bien établi que l'électron doit respecter une certaine distance de son noyau en fonction d'une certaine longueur d'onde, plus exactement un multiple de celle-ci. Or l'électron en tant qu'onde est soumis à l'effet Doppler et cette longueur d'onde se contracte sur l'axe du déplacement. C'est encor plus évident s'il s'agit d'ondes stationnaires. La conséquence logique et élémentaire de ceci, c'est que les liaisons moléculaires en dépendent également, ce qui explique à merveille pourquoi la matière se contracte. Hélas ! Lorentz ne disposait pas de cette explication. C'est pourquoi il n'a pas su résister à l'influence de Poincaré et d'Einstein, qui n'ont jamais admis cette hypothèse d'une contraction absolue. La Relativité. Poincaré s'est servi de ses équations symétriques pour mettre en avant dès 1904 son "Postulat de Relativité", calqué manifestement sur le Principe de Relativité de Galilée. Plusieurs années auparavant, il avait déjà énoncé ce principe en mentionnant que les phénomènes optiques étaient purement relatifs et que la matière ne saurait se contracter véritablement de cette manière. Selon lui, ce n'était qu'une illusion. Il avait tort, mais les effets prévus étant les mêmes, tout donnait à penser qu'il avait raison. Pourtant, la version de Lorentz sur la Relativité se vérifie tout aussi bien. Mais en plus, elle explique le comportement mécanique absolu de la matière, et elle est donc infiniment supérieure. Elle montre en particulier que l'observateur en mouvement est victime d'une mystification, mais pas celui qui est au repos. Ce dernier jouit donc d'une situation privilégiée. Et elle montre surtout que la Relativité est en faveur de l'éther. La masse active et réactive. Puisque cette page traite de l'effet Doppler, il serait dommage de ne pas mentionner que selon Lorentz, la masse et donc l'inertie doit augmenter avec la vitesse. Il s'agit d'une autre conséquence des transformations de Lorentz, et donc de l'effet Doppler. C'est pourquoi il est facile de calculer cette augmentation de masse en se référant à cet effet Doppler particulier impliquant un ralentissement de la fréquence. On y parvient en séparant la masse de la matière en deux parties. On obtient des masses actives et réactives :
Le phénomène de l'action et de la réaction dépend de facteurs qui dérivent de l'effet Doppler selon Lorentz. L'énergie totale de la matière au repos ou en mouvement vaut toujours : E = (a + r) m c 2. L'énergie cinétique de la matière en mouvement vaut : E = (a + r – 1) m c 2. Le total de ces facteurs selon : gamma = a + r explique aussi l'augmentation de la masse, une découverte de Lorentz. Les propriétés et la mécanique de la matière s'expliquent donc par l'effet Doppler. C'est une preuve irréfutable que la matière est faite d'ondes.
La loi de l'action et de la réaction. Dans ces condition, il devient clair que l'action et la réaction ne sont pas égales dans l'absolu. On démontre aussi à la page sur l'énergie cinétique qu'une boule de billard est en mesure d'en déplacer une autre uniquement à cause de l'effet Doppler, qui comprime les ondes. Cette compression des ondes se traduit par une augmentation de leur énergie, qui s'avère être tout simplement de l'énergie cinétique : E = (a + r – m) c 2 = (gamma * m – m) c 2 Le Scanner du Temps. En mars 2004, j'ai inventé un dispositif fabuleux qui permet de reproduire les transformations de Lorentz sur une base composite, à référentiels multiples, que j'ai appelé le Scanner du Temps. D'une part, ce dispositif transforme un émetteur d'ondes sphériques en émetteur mobile dont les ondes sont affectées de l'effet Doppler. Il peut également faire l'inverse, soit annuler l'effet Doppler, tout simplement en inversant le sens du balayage. Cela correspond donc aux équations symétriques de Poincaré D'autre part, ce même dispositif est capable de transformer un référentiel cartésien au repos en système mobile, ce qui inclut des horloges affichant les heures. Là aussi, il peut faire l'inverse. En particulier, ce processus permet de mieux comprendre le "temps local". Mais le plus étonnant, c'est qu'il est capable de traiter simultanément de nombreux référentiels préalablement transformés, en une seule opération ! |
|
|
Manifestement, les transformations de Lorentz ont un lien avec l'effet Doppler.
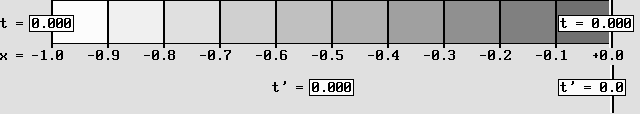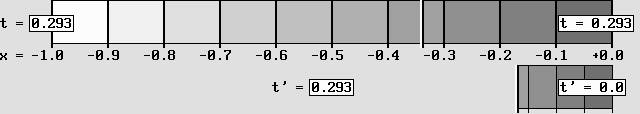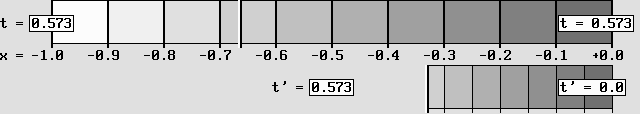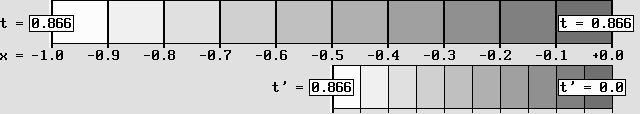
Le dispositif produit à la fois une contraction, un ralentissement des horloges et des heures locales.
Le simple fait de balayer la scène dans le sens opposé produit l'effet inverse.
Cela reproduit la fameuse réciprocité typique des transformations de Lorentz.

Ici, le système montré à gauche est accéléré à 0,866 c (à droite).
C'est ainsi qu'un roue dentée tournant sur une base au repos devrait se comporter réellement.
Il est clair que les équations de Lorentz sont incapables de réaliser autant de transformations simultanément.
Par ailleurs, la Relativité d'Einstein mène à de nombreux paradoxes (ici, celui d'Ehrenfest est levé), pour ne pas dire de contradictions.
Au contraire, le Scanner du Temps est remarquablement cohérent et logique, tout comme la Relativité de Lorentz.
| 01 | 02 | 03 | 04 | Vous êtes ici. | 06 | 07 | 08 | 09 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 |
|
Gabriel LaFrenière, Bois-des-Filion en Québec. Sur l'Internet depuis septembre 2002. Dernière mise à jour le 19 janvier 2010. Courrier électronique : veuillez consulter cet avis. La théorie de l'Absolu, © Luc Lafrenière, mai 2000. La matière est faite d'ondes, © Gabriel Lafrenière, juin 2002. |
ANTONIVS·MORO·BRVTVS·EST
(Antoine Moron est un abruti)