LA MASSE ACTIVE ET RÉACTIVE
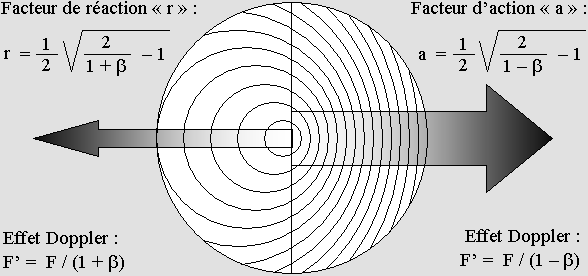
Le phénomène de l'action et de la réaction dépend de facteurs basés sur l'effet Doppler.
L'énergie cinétique de la matière en mouvement, m étant la masse au repos, vaut : E = (a + r – 1) m c 2.
L'énergie totale de la matière au repos ou en mouvement vaut toujours : E = (a + r) m c 2.
Le total de ces facteurs correspond au facteur gamma et explique l'augmentation de la masse, une découverte de Lorentz : gamma = a + r .
Les propriétés et la mécanique de la matière s'expliquent donc par l'effet Doppler.
C'est une preuve irréfutable que la matière est faite d'ondes.
![]()
![]() Page d'accueil :
La
matière est faite d'ondes.
Page d'accueil :
La
matière est faite d'ondes.
LA MÉCANIQUE DE NEWTON REVUE ET CORRIGÉE
|
L'action et la réaction dépendent de l'effet Doppler. Les termes "masse active" et "masse réactive" figuraient dans la version révisée de mon ouvrage La théorie de l'Absolu publiée en mai 2001. J'en avais donné la valeur selon les équations suivantes :
Bien qu'elles soient correctes selon le point de vue d'alors, ces équations ne mettent pas en évidence le fait que la masse active dépend exclusivement de l'effet Doppler avant (1 – bêta), alors que la masse réactive dépend plutôt uniquement de l'effet Doppler arrière, qui vaut (1 + bêta). En mars 2005, je suis enfin parvenu à relier directement la mécanique de la matière à l'effet Doppler avant et arrière selon 1 – bêta et 1 + bêta. En effet, en révisant les formules de base de l'effet Doppler, je me suis rendu compte des équivalences suivantes : (1 + bêta) / (1 – bêta) = 2 / (1 – bêta) – 1 (1 – bêta) / (1 + bêta) = 2 / (1 + bêta) – 1 J'ai donc obtenu ces équations à une seule variable (bêta), qui figurent sur le diagramme montré plus haut : a = (2 / (1 – bêta) – 1) 1 / 2 / 2 r = ( 2 / (1 + bêta) – 1) 1 / 2 / 2 ...sans réaliser sur le moment que j'avais déjà mis au point des équations à deux variables (bêta et g) plus simples : a = g / 2 (1 – bêta) r = g / 2 (1 + bêta) Par exemple : bêta = 0,866 et g = 0,5 a = 1,866 r = 0,134
Mes équations précédentes le laissaient entrevoir, mais désormais les facteurs d'action et de réaction sont rattachés spécifiquement à l'effet Doppler avant (1 – bêta) et à l'effet Doppler arrière (1 + bêta). Il s'agit d'un renforcement considérable de mon argumentation. Je rappelle que le facteur gamma de la Relativité vaut très simplement : gamma = a + r. C'est une preuve irréfutable que toute la mécanique de la matière et toutes ses propriétés sont assujetties à l'effet Doppler, ce qui suggère fortement que la matière est faite d'ondes.Isaac Newton et Poincaré. La mécanique de Newton est tout à fait remarquable. Contrairement à ce que la théorie de la Relativité d'Albert Einstein laissait croire, elle demeure pertinente à la condition de tenir compte de la nouvelle donne. Le point important, c'est que les ondes subissent l'effet Doppler dès qu'elles sont émises ou reçues à l'intérieur d'un système qui se déplace à travers l'éther. Newton ignorait que la matière est faite d'ondes. Il ne pouvait pas savoir qu'il devait tenir compte de l'effet Doppler si la vitesse d'un corps n'est plus négligeable comparativement à celle de la lumière. Il y a donc lieu de corriger sa mécanique en conséquence, mais rien de plus. Isaac Newton demeurera le grand parmi les grands. Mais il devra désormais partager sa gloire avec Lorentz et Henri Poincaré, et cette page en fera la preuve. La mécanique ondulatoire. Comme les précédentes, cette page traite de la mécanique ondulatoire. Elle sera consacrée presque exclusivement au phénomène de l'action et de la réaction, en rapport avec la masse, l'énergie, les forces et l'inertie. C'est Henri Poincaré qui a pressenti cette mécanique nouvelle : « Peut-être devrons-nous construire toute une mécanique nouvelle que nous ne faisons qu'entrevoir, où l'inertie croissant avec la vitesse, la vitesse de la lumière deviendrait une limite infranchissable ». La mécanique d'Albert Einstein, si l'on peut parler de mécanique dans ce cas, s'avère complexe et absolument irrationnelle. Il s'agit à toutes fins pratiques d'une théorie mystique qui n'est ni explicable ni modifiable. Or non seulement celle de Lorentz et de Poincaré s'explique, mais elle est hautement perfectible, tout simplement parce qu'ils n'ont fait qu'en jeter les bases. Si nous mettons tous l'épaule à la roue, nous obtiendrons une mécanique plus simple qui se vérifie aussi facilement qu'elle s'explique. La mécanique de la matière est la mécanique des ondes, et tout indique qu'on pourra y intégrer les lois et les formules de Newton le plus naturellement du monde. |
LA MASSE ACTIVE ET LA MASSE RÉACTIVE
|
Parce qu'elle n'implique que l'effet Doppler, l'augmentation de la masse d'un objet peut se calculer très simplement. On peut partager cette masse en deux parties : la partie active et la partie réactive. Il s'agit de la puissance des ondes qui se propagent dans le sens du déplacement et en sens inverse. Prenons comme exemple une vitesse de 0,866c, soit 86,6% de celle de la lumière.
On a donc selon Lorentz : bêta = 0,866 ; g = 0,5 ; gamma = 2. Dans cet exemple, la masse au repos m sera fixée à 10 kg : m = 10. Le facteur gamma valant 2, Lorentz prévoit que la masse totale M (noter la majuscule) sera portée à 20 kg à cette vitesse, soit selon : M = gamma * m.On sait que l'énergie de la matière a été évaluée selon : E = mc2, mais il se peut que l'énergie réelle de l'électron au repos soit supérieure. En effet, même si l'électron au repos présente une symétrie radiale tous azimuts, son énergie cinétique s'il se déplace s'exerce uniquement selon l'axe de son déplacement. Il est évident que les ondes transversales n'ont aucun effet. On sait que cet effet transversal n'était pas clair vers 1905 et que les résultats expérimentaux étaient parfois contradictoires. Nul doute qu'on corrigera un jour cette lacune, mais pour l'instant il suffit de distinguer les ondes qui se propagent vers l'avant de celles qui se propagent vers l'arrière. On divise donc d'abord la masse en deux moitiés, l'une active et l'autre réactive, car au départ elles valent chacune 0,5 kg lorsqu'elles sont au repos. C'est pourquoi les formules indiqueront une division par deux. Mais à cette vitesse, il faut aussi réduire la valeur de l'énergie présente selon le facteur g de Lorentz, sachant que l'énergie d'une onde est proportionnelle à sa fréquence. Les transformations de Lorentz prévoient en effet que cette fréquence sera réduite de moitié à cette vitesse selon le facteur g. De plus, si cette matière accélère, chacune des deux moitiés subit l'effet Doppler en sens inverse. Alors les facteurs d'action et de réaction correspondent aux équations suivantes : |
a = g / 2 (1 – bêta) r = g / 2 (1 + bêta)
Le facteur d'action : a = 1,866 Le facteur de réaction : r = 0,134
La masse active : a * m = 18,66 kg La masse réactive : r * m = 1,34 kg
La masse totale à cette vitesse : a * m + r * m = 20 kg.
L'énergie cinétique : E = (a + r – 1) c 2 = c 2 = 9 * 10 16 joules pour chaque kilogramme de matière au repos.
Le gain de masse : G = a + r – 1 = gamma – 1 = 1 kg pour chaque kilogramme de matière au repos.
Cela confirme que l'énergie cinétique correspond purement et simplement au gain de masse.
La masse totale : M = a + r = gamma = 2 kg pour chaque kilogramme de matière au repos.
|
Ce calcul montre que la masse totale M vaut bien gamma * 10 = 20 kg tel que prévu par Lorentz, selon le facteur gamma. Le diagramme ci-dessous montre clairement pourquoi la masse de la matière augmente selon l'effet Doppler, mais il montre surtout pourquoi l'action et supérieure à la réaction. On sait que l'énergie d'une onde augmente avec sa fréquence. La contraction des ondes vers l'avant est illimitée. Ainsi, la matière qui se déplace à des vitesse voisines de celle de la lumière peut emmagasiner des quantités pratiquement illimitées d'énergie : |

La masse active et réactive explique l'action et la réaction.
Ce diagramme montre un système qui se déplace à la moitié de la vitesse de la lumière.
Les formules suivantes sont plus simples que celles indiquées ci-dessus :
a = g / 2 (1 – bêta) r = g / 2 (1 + bêta)
Ce calcul explique aussi l'augmentation de la masse, mais aussi son énergie, qui se traduit par des forces.
|
La matière présente toutes les propriétés des ondes stationnaires sphériques. Il convient de souligner que le rapport entre les facteurs d'action et de réaction est le même que celui qui existe entre l'effet Doppler avant et arrière, peu importe que la fréquence diminue ou non selon les prévisions de Lorentz : |
|
|
Le rapport entre les facteurs d'action et de réaction est proportionnel à l'effet Doppler.
a / r = 13,93
(1 + bêta) / (1 – bêta) = 13,93
C'est indiscutable, la masse d'un corps augmente en fonction de sa vitesse à cause de l'effet Doppler.
Il en résulte un gain dans l'action qu'un tel corps exerce sur un autre, et cette action s'exerce par des ondes.
Fondamentalement, c'est ce qui explique qu'une boule de billard plus rapide exerce une pression plus forte sur une autre.
|
Les valeurs 1 + bêta et 1 – bêta correspondant à l'effet Doppler, tout comme celles des facteurs d'action et de réaction, elles indiquent ici encore une fois, et hors de tout doute, que la matière se comporte strictement comme le font les ondes stationnaires sphériques.Je tiens à rappeler ici que M. Milo Wolff fut le premier à affirmer que la matière est faite d'ondes stationnaires sphériques. Il avait aussi affirmé que la masse de la matière doit augmenter selon l'effet Doppler, mais son calcul me semble bizarre, d'autant plus qu'il ne mentionne pas que cette augmentation avait déjà été prévue correctement par Lorentz. |
LES FORCES ACTIVES ET RÉACTIVES
|
Il s'agit maintenant de montrer que, puisque les ondes véhiculent de l'énergie, ces masses actives et réactives représentent aussi de l'énergie, ce qui implique des forces actives et réactives. Répétons que pour un observateur qui se situe dans un référentiel mobile, l'effet Doppler ne peut pas être détecté. C'est pourquoi deux électrons y réagiront mutuellement comme s'ils étaient au repos. Les électrons sont victimes des mêmes illusions que nous. Leur comportement mutuel dépend de leur vitesse relative. Le comportement mécanique de la matière est donc relatif. Comme Henri Poincaré l'avait prédit, les lois des phénomènes physiques semblent donc les mêmes quelle que soit la vitesse du référentiel. Même s'il ignorait pourquoi, sa "mécanique nouvelle" s'avère tout à fait conforme à ses prévisions. Il n'empêche que, comme la masse, ces forces sont sujettes à l'effet Doppler d'une manière absolue. C'est évident sur la figure ci-dessous, qui représente les ondes stationnaires-mobiles d'un électron qui se déplace à la moitié de la vitesse de la lumière : |
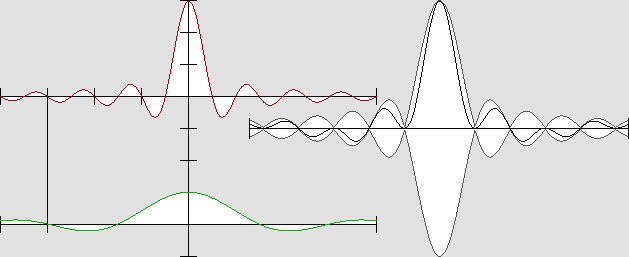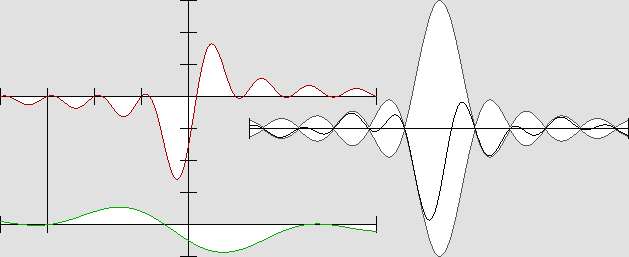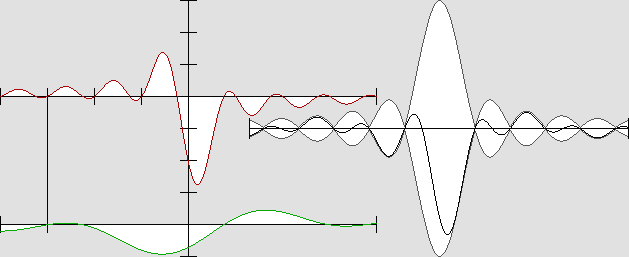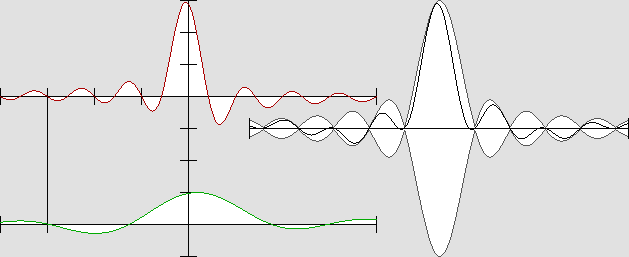
Les ondes stationnaires-mobiles au voisinage du noyau central de l'électron en mouvement.
Les ondes de la masse active se déplacent vers la droite, celles de la masse réactive, vers la gauche.
Comme celui des longueurs d'onde, le rapport R des amplitudes A varie selon : R = (1 + bêta) / (1 – bêta)
On a ici : v = 0,5 c et donc : R = 3 ; bêta = 0,5 ; A1 = 75 % ; A2 = 25 % ; A1 / A2 = 3.
|
Ce système est montré dans son référentiel mobile, ce qui signifie qu'il faut le suivre à la même vitesse pour pouvoir l'observer de cette manière. Il représente les ondes actives et réactives d'un électron, mais seulement telles qu'elles se comportent le long de l'axe du déplacement. Il faut souligner que non seulement la longueur des ondes, mais aussi leur amplitude n'est pas la même dans les deux sens. C'est en analysant cette particularité que je suis parvenu aux formules des facteurs d'action et de réaction. Il s'agit de réaliser que ce système se déplace à la moitié de la vitesse de la lumière pour des raisons mécaniques, et il suffit donc de repérer quelles sont les grandeurs qui produiront la force requise sur le noyau central de l'électron : c'est l'inertie. On remarque qu'apparemment, les ondes comprimées se déplacent trois fois plus lentement que les ondes dilatées. De cette manière, leur cadence (et non pas leur fréquence absolue) est exactement la même. C'est ce qui explique que l'effet Doppler est imperceptible vu de l'intérieur du même système mobile. L'animation ci-dessous montre plutôt des ondes stationnaires planes, dont la longueur d'onde, mais aussi l'amplitude diffèrent : |
|
|
Les ondes stationnaires-mobiles planes : v = 0,5 c ; bêta = 0,5 ; A1 = 65 % ; A2 = 35 %.
Ni la fréquence des ondes ni leur amplitude ne sont les mêmes vers l'avant et vers l'arrière.
L'observateur se déplace vers la droite en suivant ce système mobile.
Remarquer comment les nœuds sont bousculés sous l'influence des forces opposées.
|
Cette animation a le mérite de montrer que les nœuds et les ventres des ondes appelées parfois "partiellement stationnaires" ne se déplacent pas uniformément si, en plus de leur amplitude, leur fréquence n'est pas la même. Ils sont en quelque sorte bousculés en raison de la puissance relative des ondes actives et réactives. La pression de radiation. C'est ce qui explique que le noyau central d'un électron est très sensible à la pression de radiation. Si des ondes additionnelles étrangères à celles de l'électron interviennent, l'inertie de ce dernier n'est plus préservée. Il peut en être aussi bien accéléré que ralenti. Il peut même changer de direction. Le diagramme ci-dessous a été réalisé par ordinateur, et uniquement à l'aide du principe de Huygens. Ce principe n'ayant jamais été invalidé, il s'agit ici de la prédiction la plus fiable de ce que des ondes hémisphériques convergentes devraient produire. Je suis très fier de cette animation, car tout indique qu'aucun opticien n'était encore arrivé à réaliser une vue similaire. Il s'agit véritablement d'une tache d'Airy en vue longitudinale, donc comprenant l'axe optique et non pas le plan focal. On suppose ici que l'ouverture de l'objectif fait 180°, ce qui est très possible si cet objectif est un miroir ellipsoïde ou paraboloïde. Pour ceux qui auraient des doutes, ajoutons que ce phénomène peut facilement être observé et vérifié à l'aide de sons ou d'ultrasons réfléchis par un ellipsoïde de révolution, si quelqu'un voulait s'en donner la peine : |
|
|
La masse active d'un électron au repos. Les ondes proviennent uniquement de l'hémisphère gauche.
Remarquer comment le noyau central est déporté latéralement sous la pression des ondes.
Si l'électron est au repos, cet effet est neutralisé par les ondes de la masse réactive, qui est identique.
Mais dès que la masse réactive faiblit, le noyau central est constamment déplacé vers l'avant.
|
Les ondes de l'électron au repos ne subissent pas l'effet Doppler, et c'est pourquoi la masse active est égale à la masse réactive. L'effet Doppler possède la propriété de modifier à la fois la longueur d'onde et l'amplitude, et alors l'électron adopte la vitesse appropriée : c'est l'inertie. L'inertie. Ce phénomène explique donc la loi de l'inertie. Il s'agit d'une découverte importante, qui avait échappé non seulement à Galilée et à Newton, mais aussi à Lorentz et à Poincaré. On sait que la première loi de Newton, soit le fameux Principe d'Inertie, a d'abord été énoncée par Galilée. Il avait constaté qu'une fois mis en mouvement à une certaine vitesse, un corps adoptait définitivement cette vitesse sur une trajectoire rectiligne, à moins qu'il ne soit soumis à une force. Ce comportement semble aller de soi, mais encore fallait-il l'expliquer. Il fallait aussi expliquer pourquoi et comment cette force agit, ce qui n'est pas évident. C'est encore moins évident quand vient le temps de concilier l'existence de l'éther avec le fait que la matière qui se déplace doit constamment le traverser. Au 19e siècle, on avait constaté que : « L'éther ne s'oppose pas au mouvement ». Avouons que la loi de l'inertie pouvait en effet sembler incompatible avec la présence de l'éther. Mais le fait que la matière soit faite d'ondes permet maintenant de lever cette objection d'une manière indiscutable. Désormais, parce que c'est sa seule propriété connue, on peut affirmer que puisque l'éther permet aux ondes de se propager, c'est lui qui rend possible le mouvement des ondes sphériques appelées à tort "stationnaires". Désormais, nous pouvons affirmer que l'éther permet le mouvement. Il ne s'y oppose pas.
LA LOI DE L'ACTION ET DE LA RÉACTION Le fait de séparer la masse en parties actives et réactives permet donc d'expliquer de manière très convaincante le phénomène de l'action et de la réaction, car c'est uniquement la différence de vitesse qui importe et non la vitesse absolue. Deux boules de billard qui entrent en collision frontale mettent en jeu ces masses respectives. Il faut en premier lieu remarquer que lorsque deux boules de billard entrent en "contact", il n'y a pas de contact véritable. S'il y a action et réaction, c'est parce que les électrons négatifs présents autour des atomes et des molécules deviennent à faible distance beaucoup plus rapprochés les uns des autres que les protons positifs du noyau. Dès que la différence se fait sentir, il en résulte une force de répulsion de nature essentiellement électrostatique, et il faut bien comprendre qu'un tel champ résulte en fait de la composition des ondes des électrons. C'est pourquoi le résultat est assujetti à l'effet Doppler. Le choc élastique frontal. Ici, il sera uniquement question d'un choc élastique, car autrement une partie de l'énergie est convertie en chaleur, par exemple lorsque deux sacs de sable sont projetés l'un contre l'autre. La mécanique ondulatoire proclame que toutes les forces (et donc aussi la pression par contact) agissent par des ondes, et que ces ondes agissent à la vitesse de la lumière par la pression de radiation. On sait par l'expérience que si une boule de billard heurte de plein fouet une autre qui est immobile, celle-ci sera propulsée à la même vitesse, et que la première en sera immobilisée. Il faut réaliser que s'il en est ainsi, c'est parce que leurs électrons s'échangent, dans les deux sens, des ondes qui ont une masse. C'est un peu comme si les occupants de deux embarcations s'échangeaient mutuellement des petites pierres en les projetant dans l'autre embarcation, tant qu'ils sont à proximité, d'où l'action et la réaction. Mais ici, ce sont plutôt des ondes stationnaires qui agissent. D'une part, ces ondes se déplacent à la vitesse de la lumière, qui est constante. Cela signifie que l'énergie qui en résulte se calcule systématiquement en fonction de la vitesse de la lumière. D'autre part, les ondes provenant d'une boule de billard qui se déplace subissent l'effet Doppler. Sachant que l'énergie d'une onde est inversement proportionnelle à sa longueur d'onde, il est facile d'en déduire que cette énergie est supérieure vers l'avant et inférieure vers l'arrière. Un transfert de masse. L'énergie des ondes provenant des électrons de la boule de billard qui se déplace est donc supérieure vers l'avant. Par contre, au début du choc, l'autre boule qui est au repos ne peut lui opposer que des ondes qui ne subissent pas l'effet Doppler. C'est ce déséquilibre qui provoque l'augmentation ou la réduction de la masse. Il se produit véritablement un transfert de masse. Je ne suis pas mathématicien et ma connaissance du calcul différentiel et intégral est limitée. Toutefois, il suffit d'examiner attentivement la "méthode des fluxions" de Newton pour en comprendre le principe, ce qui permet à tout bon programmeur d'écrire un algorithme qui réalise l'équivalent. Il n'est pas nécessaire d'introduire la notion de "conditions aux limites", le nombre d'itérations pouvant très bien réduire la marge d'incertitude. J'ai donc pris la peine d'écrire un tel algorithme, d'ailleurs très simple, pour vérifier la justesse de cette explication, et les résultats sont concluants. On peut procéder de différentes façons, mais dans le but de respecter ce qui se passe vraiment, j'ai retenu la méthode qui consiste à retrancher d'abord une infime fraction de la masse active du projectile, puis d'ajouter cette même quantité à la masse réactive de la cible. Si celle-ci était au repos, cette masse réactive devient supérieure à la masse active et elle doit par la suite être considérée comme la masse active, qui détermine le sens du déplacement. Alors la masse active du projectile s'ajoute à la masse active de la cible. Si la masse et donc l'énergie de l'électron est constante pour une vitesse donnée, c'est parce qu'il dispose d'une quantité constante d'énergie, qui est présente dans l'éther sous forme d'ondes planes. Alors, selon la formule donnée plus haut, la réaction ne peut valoir que : r = 1 / 4 a de manière à respecter le rapport d'énergie compatible avec l'effet Doppler. On obtient ainsi de nouvelles valeurs des facteurs a et r pour le projectile et la cible, et il devient possible de calculer leur nouvelle vitesse selon : bêta = (a – r) / (a + r). Il faut un grand nombre d'itérations pour arriver à un résultat acceptable, comme c'est le cas pour la méthode d'Euler. Cette méthode était lente autrefois, mais depuis que les processeurs fonctionnent dans les Gigahertz, elle est étonnamment efficace. Comme je l'ai mentionné plus haut, j'utilise une méthode semblable pour produire des diagrammes animés stupéfiants de la tache d'Airy. Puisqu'on ne trouve rien de comparable sur l'Internet, on peut penser que les opticiens n'y arrivent pas et que le calcul différentiel et intégral est dépassé. Nos ordinateurs ultra-rapides font mieux... Dans le but de faire la démonstration que la mécanique de l'action et de la réaction dépend bel et bien de la masse active et réactive, j'ai donc réalisé le diagramme animé ci-dessous, qui montre de quelle manière se déroule le processus : |

Un choc frontal entre deux boules de billard dont la masse m au repos est de 1 kg.
Bien évidemment, on postule que ces boules sont élastiques et indestructibles.
La masse totale M de la boule qui provient de la gauche vaut 2 kg car elle se déplace à la vitesse de 0,866 c.
Après le choc, cette boule s'est immobilisée, et l'autre boule a été propulsée à la vitesse de 0,866 c.
|
Ce calcul montre très clairement qu'à mi-parcours, lorsque la vitesse des deux boules est la même, leur masse totale T n'atteint que 2,79 kg au lieu des 3 kg initiaux. À ce moment, la différence (delta) de 0,21 kg doit bien se trouver quelque part. En conformité avec la loi de la conservation de la masse et de l'énergie, cette masse ne peut pas se perdre. Manifestement, elle se trouve temporairement dans le champ de force. Un transfert d'énergie. Il est intéressant de constater que la vitesse des ventres et des nœuds de ces ondes stationnaires se situe à mi-chemin des vitesses des deux boules, car elle dépend de l'effet Doppler de la masse active de l'une comparativement à l'effet Doppler de la masse réactive de l'autre : bêta'' = (a – r ') / (a + r ') Au départ, la vitesse de ces nœuds est donc ici de 0,577 c et il se produit un délai dans le transfert de l'énergie entre les deux boules. En effet, à l'intérieur des ondes pseudo-stationnaires, l'énergie se transmet à la même vitesse que celle de leurs nœuds. Elle demeure stationnaire si les ondes sont parfaitement stationnaires. C'est ce délai qui explique qu'une partie de l'énergie cinétique se situe temporairement en dehors des deux boules. Si celles-ci sont immobilisées, et c'est le cas des électrons qui constituent les quarks du neutron ou du proton, cette énergie demeure captive indéfiniment à l'intérieur des champs gluoniques. C'est pourquoi je pense qu'un neutron est fait de seulement trois quarks, c'est à dire trois couples d'électrons dont l'axe coïncide avec les trois axes de Descartes, de manière à ce que l'effet d'attraction des 15 champs gluoniques qui en résultent les maintiennent ensemble. La masse du neutron, soit 1838 fois la masse d'un seul électron, provient essentiellement de l'énergie cinétique accumulée des six électrons qui le composent. Il est donc clair que les neutrons ne peuvent se construire spontanément qu'en présence de d'électrons et de positrons, qui s'attirent au lieu de se repousser. Leur réunion à haute vitesse produit des quarks et des antiquarks par paires, accompagnés de champs gluoniques, et non pas leur annihilation comme on le prétend actuellement. Cette énergie captive explique parfaitement les forces nucléaires. Elle se traduit par une masse et une inertie, ce qui signifie que les champs électrostatiques stables et les champs gluoniques possèdent aussi une masse et une inertie. C'est pour ainsi dire de l'énergie cinétique en conserve. De plus, la fréquence de ces ondes stationnaires varie selon la différence de vitesse, soit selon la loi de l'addition des vitesses de Poincaré. Cette fréquence qui varie selon la vitesse relative apparente (et non pas absolue) a certainement un lien avec l'onde de de Broglie, celle-ci résultant sans doute des battements entre des ondes dont la fréquence n'est pas la même. On notera que les zones qui déterminent ces battements se déplacent toujours à une vitesse supérieure à celle de la lumière. Il s'agit de l'onde de phase, qui correspond au décalage horaire selon Lorentz. Cela correspond aussi à la vitesse de balayage de mon scanner du temps, et donc à : 1 / bêta, en secondes-lumière par seconde, ou encore en longueur d'onde par période. Bêta est ici la vitesse normalisée des nœuds du champ électrostatique et non celle des électrons. C'est donc par l'intermédiaire du champ électrostatique que les forces actives et réactives agissent lors d'un choc ou d'une influence à distance. La différence de masse se trouve temporairement stockée à l'intérieur de leurs ondes stationnaires, qui sont essentielles pour effectuer le transfert de l'énergie. L'animation montrée ci-dessous est encore plus révélatrice, puisqu'elle montre un choc frontal pendant lequel, l'espace d'un instant, la totalité de l'énergie cinétique est stockée dans les ondes stationnaires du champ électrostatique : |

Ce choc frontal implique deux boules de billard qui se déplacent en sens contraire à la vitesse de 0,866 c.
On a postulé qu'au moment où elles s'immobilisent, ces boules ont une masse d'un seul kilogramme.
La masse totale d'origine étant de 4 kg, la différence (delta) de 2 kg devient la masse du champ électrostatique.
Celui-ci agit comme un ressort qui se détend. Il peut propulser de nouveau les deux boules à la vitesse de 0,866 c.
|
Le choc oblique. L'énergie échangée est réduite lors de collisions obliques, et il est facile de deviner que c'est parce que l'effet Doppler varie de manière sinusoïdale selon la direction : lambda' = lambda * (1 – bêta * cos phi) L'angle phi est supposé nul vers l'avant. Il atteint 180° vers l'arrière. Ces considérations montrent que les forces impliquées lors d'un choc oblique devraient bel et bien varier selon le théorème de Pythagore comme Newton l'avait montré. Toutefois, à des vitesses proches de celle de la lumière, l'angle des ondes actives ou réactives doit être rapporté à leur point d'origine. On peut évaluer la correction nécessaire en traçant, autour du projectile et de la cible, des ellipsoïdes de révolution aplatis selon Lorentz. Alors le point de contact indique l'angle correct. L'action et la réaction sont assujetties à l'effet Doppler. Généralement, on peut considérer que l'ancienne loi de l'action et de la réaction demeure valide. « À toute action correspond une réaction de même grandeur mais de sens opposé. » Mais cette loi s'avère inexacte si la différence de vitesse n'est plus négligeable comparativement à celle de la lumière. Le problème survient parce que l'observateur qui effectue l'expérience se considère lui-même au repos en vertu de la loi de la Relativité, alors que les deux corps qu'il observe ont parfois leur vitesse propre. Bien évidemment, cette vitesse ne peut être évaluée que selon le point de vue de l'observateur, car du point de vue de chacun de ces objets, les données seraient contradictoires. Il vaut mieux en définitive déterminer au préalable un référentiel privilégié situé au centre d'inertie de ces deux corps, et qui sera présumé être au repos dans l'éther. Cela permettra d'observer que ces deux corps devront se heurter puis rebrousser chemin comme si le champ de force exerçait exactement la même force dans les deux directions opposées. Cela conduit à un principe de double action parfaitement exact. À cause de sa réciprocité caractéristique, on pouvait à juste titre reprocher à la théorie de la Relativité d'Albert Einstein d'être incapable de concilier simultanément trois systèmes de référence. Les deux équations symétriques de Henri Poincaré s'avèrent dans ce cas tout aussi impraticables. Si quelqu'un le lui avait fait remarquer, je suis persuadé que Poincaré aurait fait marche arrière. Au lieu de mettre l'existence de l'éther en doute, il aurait sûrement opté pour la version absolue de Lorentz. Il arrive qu'une onde exerce une action négative, donc une force d'attraction. C'est le cas de l'effet d'ombre, de la gravité, des charges électriques opposées, etc. Alors la réaction est également négative. Il faut comprendre que pour des raisons mécaniques, il n'est jamais possible de justifier un effet d'attraction. Il ne peut exister qu'une force positive. Dans le cas d'une force d'attraction, ce sont en fait les ondes planes de l'éther venant en sens opposé qui exercent la véritable pression. D'un point de vue absolu, l'action et la réaction ne sont pas simultanées à cause de l'effet Doppler, mais du point de vue du référentiel privilégié montré ci-dessus, elles le sont toujours. En effet, les transformations de Lorentz prévoient des heures locales qui rétablissent la simultanéité virtuelle des événements. Le processus de l'action et de la réaction permet également de justifier les lois de la conservation de la masse et de l'énergie. On constate en effet que, dans notre exemple, la masse totale de deux corps avant et après un choc frontal ne varie pas. Dans les faits la moitié de la masse du corps qui se déplace, qui est responsable de l'énergie cinétique, passera dans celle de celui qui est au repos. En présumant qu'il s'agit d'un choc élastique, c'est celui-ci qui sera propulsé à la vitesse de 0,866 c et l'autre en sera immobilisé. Les causes et les effets. Il faut éviter de confondre la réaction avec l'effet, puisque les effets ne peuvent pas chevaucher leur propre cause et encore moins la précéder. Il y a là matière à discussion, et il est plus que probable qu'on en discutera encore dans mille ans. Pour l'instant, la présente version de la mécanique ondulatoire se borne à proposer un nouveau principe de Causalité faisant intervenir les ondes de l'éther : « Tout effet a une cause, tout effet devient une cause, et les causes agissent par des ondes à la vitesse de la lumière ». |
|
L'analogie des corpuscules. Étonnamment, comme en font foi les formules montrées plus haut, tout se passe comme si, à l'intérieur de la matière, cette énergie se déplaçait constamment à la vitesse de la lumière. Cette idée d'un déplacement de l'énergie conduit à une analogie fascinante : la matière agit ou réagit comme si elle contenait une infinité de corpuscules matériels dotés d'énergie cinétique, qui se déplaceraient en tous sens en se heurtant constamment selon une moyenne qui correspond à la vitesse de la lumière. À cause de la loi de l'entropie, il se produit une uniformisation de la vitesse moyenne des corpuscules, quelle que soit la vitesse de l'objet. Toutefois, en comparaison de leur vitesse d'origine alors que l'objet est présumé au repos, leur vitesse moyenne est celle de l'objet en mouvement plus leur vitesse d'origine. L'énergie cinétique totale des corpuscules augmente donc avec la vitesse de l'objet. Cela simule l'augmentation de masse d'une manière très imagée. Non seulement les corpuscules se heurtent entre eux, mais ils heurtent les parois de l'objet. C'est en heurtant ses parois qu'ils communiquent à l'objet une certaine vitesse. C'est pourquoi l'objet se déplace, et qu'il le fait à une vitesse constante. Comme on l'a vu plus haut, les ondes agissent de cette manière sur le noyau central d'un électron, et c'est ce qui explique son inertie. Lors d'un choc avec un autre objet, ces corpuscules seraient capables de passer du projectile à la cible en plus grand nombre, de manière à communiquer à cette cible une partie de la masse du projectile. C'est dû au fait que les corpuscules qui se déplacent vers l'avant sont plus rapides dans le projectile que dans la cible. C'est le contraire en sens inverse. Alors le projectile s'en trouve ralenti et la cible, accélérée. Fondamentalement, c'est ainsi que la masse active et réactive fonctionne. L'analogie des corpuscules montre que les ondes présentent des similitudes étonnantes avec les corpuscules dotés d'inertie et d'énergie cinétique. Dans le cas de la lumière, on n'y voit que des ondes tant que leur longueur est grande devant les particules impliquées. Mais dès que le volume de ces particules devient non négligeable, les calculs ne fonctionnent plus et tout donne à penser qu'on est en présence de corpuscules. En fait, c'est l'électron qui est impliqué, et il s'agit véritablement d'une onde-corpuscule, tout à fait comme le prévoyait de Broglie. Boltzmann et l'entropie. On sait que la loi de l'entropie de Boltzmann dérive des calculs de Maxwell sur les anneaux de Saturne, par lesquels ce dernier avait démontré que ces anneaux étaient faits de corpuscules solides. En étudiant la chaleur, Boltzmann avait découvert pour les mêmes raisons qu'elle devait être le résultat d'une vibration des molécules et que la matière devait être faite d'atomes. D'un autre côté, le rayonnement du corps noir dépend de la température, et donc d'une vibration des molécules de la matière. Ces vibrations n'étant pas illimitées, on aboutit à ce qu'on a appelé la catastrophe ultraviolette. C'est pourquoi Max Planck, ayant trouvé la valeur de sa constante d'une manière empirique, avait constaté par la suite qu'elle dérivait de la constante de Boltzmann. Dans les trois cas, on parle donc de corpuscules qui s'entrechoquent. Le calcul doit tenir compte de leur masse et de leur énergie cinétique, selon les lois de Newton. La Relativité est ici formellement exclue puisqu'elle ne s'applique qu'à des ondes. Il est évident que la vitesse de ces particules doit obéir à la distribution normale, qui affecte la forme d'une cloche. Bien évidemment, on obtient une courbe asymétrique si les extrêmes varient entre un minimum et un maximum, et c'est effectivement le cas ici. Malgré tout ce qu'on en dit, tout ceci est donc parfaitement simple et logique. Encore fallait-il le formuler, et la présence d'une constante n'était pas évidente. Ce fut l'œuvre de Boltzmann. L'éther et la constante de Boltzmann. Même si ce n'est peut-être pas le cas, l'éther pourrait bien être fait de particules qui s'entrechoquent. Le problème, c'est qu'il faudrait expliquer toute la mécanique de ces particules, ce qui nous ramènerait à la case départ. Huygens parlait de sphères en contact, alors que Fresnel parlait de points matériels séparés par des intervalles. Il s'agit en tous cas d'une substance homogène hautement élastique. Dans ce cas, l'éther possède peut-être une constante propre qui dérive aussi de la constante de Boltzmann, et qu'il reste à découvrir. Je précise ici que beaucoup de mes démonstrations s'appuient sur le principe de Huygens. Elles seraient tout à fait invalides autrement. Ce principe n'exige pas de telles particules, mais celles-ci sont très utiles pour justifier la propagation des ondes. Alors les calculs de Maxwell, de Boltzmann et la valeur trouvée de manière empirique par Max Planck prennent toute leur importance, même si dans les faits ils sont peut-être fondés sur des prémisses erronées. En plus clair, il se peut que la constante de Boltzmann décrive les propriétés de l'éther lui-même. Sinon, elle s'appliquerait à l'électron, qui est capable d'osciller autour de sa position selon des forces qui s'établissent par paliers successifs, et donc d'une manière discrète, quantique. Les quanta. La constante de Planck est omniprésente chaque fois qu'il faut quantifier la matière. On ne peut le faire que par étapes successives dont la valeur est toujours la même. Par contre cette constante est très nettement assujettie à la fréquence, par exemple dans le cas de la lumière, ce qui fait qu'il peut exister toute une gamme de fréquences qui ne présentent pas ces valeurs en escalier dites discrètes ou quantiques. Sans vouloir minimiser l'importance de ces découvertes, il faudrait tout de même réaliser que toutes ces belles formules ne servent qu'à calculer des particules qui s'entrechoquent. On peut très bien le faire à l'aide des statistiques, mais sans perdre de vue que dans les faits, la trajectoire réelle de chaque particule est bien déterminée. De là à penser que notre propre existence est bien déterminée, il n'y a qu'un pas, que je n'ai pas encore franchi. Il faut aussi comprendre que, à mesure qu'on avance dans l'infiniment petit, on finit par rejoindre la taille des particules ou des longueurs d'onde. Ces calculs deviennent alors de moins en moins fiables, jusqu'à devenir tout à fait erronés. Il ressort de tout ceci que la mécanique quantique ne représente pas une avenue pleine de promesses. Ce n'est qu'un aspect du fonctionnement de la matière, et elle a ses limites dans l'infiniment petit. Désormais, il faudra plutôt parler de la mécanique ondulatoire. Il n'empêche que des ondes qui se déploient sans pertes dans un milieu fermé se comportent comme les particules de Maxwell et de Boltzmann. Elles sont soumises à la loi de l'entropie, ce qui signifie qu'avec le temps elles devraient passer irrévocablement d'un état progressif à un état partiellement stationnaire, puis à un état stationnaire uniforme et permanent. La vitesse de la lumière : une limite absolue. La masse active et donc la masse totale tend vers l'infini lorsque la vitesse d'un objet approche celle de la lumière, ce qui signifie que Poincaré avait tout à fait raison en affirmant en 1904 que la vitesse de la lumière constitue une limite infranchissable. Contrairement à ce que certains prétendent, rien ne peut dépasser la vitesse de la lumière. D'une part, la matière peut l'approcher mais elle ne peut pas l'atteindre. D'autre part, toutes les forces sont transmises par des ondes et elles agissent à la vitesse de la lumière. L'action et la réaction à distance implique des effets simultanés, ce qui peut conduire facilement à des erreurs d'interprétation. Il pourrait arriver par exemple que lors d'une expérience, on agisse sur un élément intermédiaire mal connu et invisible, l'exemple le plus évident étant le champ électrostatique. Comme le champ gluonique, ce champ qui se situe dans l'espace qui sépare électrons, protons ou positrons est fait d'ondes stationnaires. Il possède une masse véritable qui le rend sensible à la pression de radiation. Il est toujours présent si la distance entre deux particules est très grande. Il est évident que le fait d'agir sur ce champ agit ensuite simultanément sur les deux particules qui l'ont créé, même si la distance qui les sépare est très grande. Dans ce cas, l'action et la réaction ne sont pas instantanées, elles sont plutôt simultanées après un délai qu'on a omis de mesurer. C'est pourquoi les observations donnent à penser qu'elles ont été instantanées et qu'elles ont donc eu lieu à une vitesse supérieure à celle de la lumière. Il faut rejeter l'hypothèse d'un action à distance supérieure à la vitesse de la lumière. Et enfin, puisque la lumière est faite d'ondes progressives et non pas de photons, elle se déplace bien évidemment à la vitesse de la lumière, et pas plus. Dès qu'elle a été émise, elle ne saurait subir a posteriori quelque influence que ce soit à partir de l'endroit où elle a été émise.Il n'y a pas d'action instantanée à distance. Si certaines expériences laissent croire le contraire, c'est que leurs résultats ont été mal interprétés. C'est d'ailleurs le cas très souvent... |
| 01 | 02 | 03 | 04 | 05 | 06 | 07 | 08 | 09 | 10 | 11 | 12 | 13 | 14 | 15 | Vous êtes ici. |
| 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 |
Gabriel LaFrenière, Bois-des-Filion en Québec. Sur l'Internet depuis septembre 2002. Dernière mise à jour le 12 septembre 2009. Courrier électronique : veuillez consulter cet avis. La matière est faite d'ondes, © Gabriel Lafrenière, juin 2002. |