LA FORCE DE COULOMB
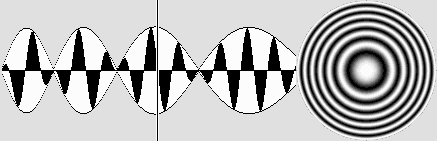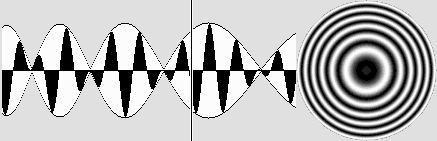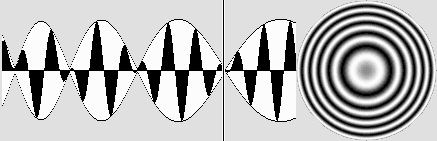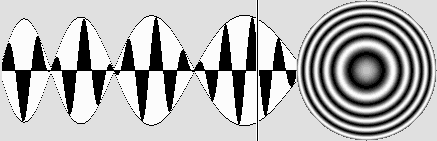
À droite, une section du champ électrostatique, qui résulte de l'addition des ondes provenant de deux particules.
Sur l'axe, ce champ rayonne des ondes dont la période est constante malgré le déplacement des particules.
Ces ondes sont constamment en phase dans le cas de deux électrons, ce qui a pour effet de les éloigner l'un de l'autre.
Elles sont plutôt en opposition de phase dans le cas d'un positron et d'un électron, d'où un effet d'attraction.
![]()
![]() Page
d'accueil : La matière
est faite d'ondes.
Page
d'accueil : La matière
est faite d'ondes.
|
Le champ électrostatique. La force de Coulomb prend sa source dans le champ électrostatique. Si les électrons rayonnent des ondes, il est clair qu'un tel champ résulte de l'addition de ces ondes. D'ailleurs, on sait très bien que les électrons présentent des propriétés ondulatoires. Le champ électrostatique est un champ de force qui contient ou transmet de l'énergie cinétique. Comme c'est le cas pour tous les autres champs de force, son fonctionnement relève de la dynamique des champs de force. Voici comment les ondes se composent si elles sont affichées sur un plan comprenant l'axe qui unit deux électrons : |
|
|
Cette image montre comment les ondes émises par deux électrons se composent.
Comme prévu, elles se recoupent sur des ellipsoïdes et des hyperboloïdes.
|
|
Cette image ne montre que les ondes stationnaires qui en résultent.
Il s'agit du champ électrostatique, qui n'est présent que dans la partie centrale.
|
Le plan central : une référence. Rappelons que l'électron est fait d'ondes stationnaires sphériques et qu'il est amplifié par les ondes qui circulent dans l'éther en permanence. Or le champ électrostatique est fait également d'ondes stationnaires, et il est lui aussi amplifié de la même manière. Il doit donc rayonner en permanence l'énergie qu'il emprunte. Il n'est pas possible à l'heure actuelle d'écrire un programme suffisamment rapide pour qu'il soit en mesure de calculer le rayonnement de ce champ électrostatique dans son entier. Ma méthode fait appel au principe de Huygens, ce qui signifie que l'ordinateur doit évaluer des millions, voire des milliards d'ondelettes de Huygens en différents points de l'espace. Mais avec le temps, il est devenu clair que cette méthode était beaucoup trop lente avec les ordinateurs actuels. Le problème, c'est qu'il faut analyser l'espace dans ses trois dimensions. Il m'a donc fallu utiliser des raccourcis et des simplifications qui soient suffisamment fiables. Je sais que personne ne voudra me faire confiance ici, et avec raison. Par contre, les diagrammes que je présente dans cette page sont vérifiables au moyen d'expériences acoustiques relativement simples. Il est très possible en effet de reproduire l'allure générale d'un champ électrostatique au moyen de deux haut-parleurs alimentés à la même source et placés face-à-face. Les ondes stationnaires et partiellement stationnaires qui se forment entre eux auront la même allure que sur l'animation montrée ci-dessus. Mais surtout, il sera aussi possible de projeter des ultrasons sur ces ondes stationnaires de manière à les amplifier. Alors ils émettront à leur tour un rayonnement particulier qui devrait correspondre à ce que mes simplifications indiquent. Dans un premier temps, en comparant différents résultats partiels, j'ai présumé que l'onde centrale, qui seule est plane et non pas hyperboloïde, permet à elle seule de prédire quelle sera l'allure générale du rayonnement de l'ensemble. Cette onde centrale comporte des ondes parfaitement stationnaires sur l'axe. Mais ensuite la période évolue du centre vers l'extérieur de la manière suivante : |

La période des ondes du plan central évolue du centre vers l'extérieur.
Noter que l'amplitude des ondes est à peu près constante, le noir représentant ici l'opposition de phase.
Vue d'un point rapproché sur l'axe, la fenêtre d'un laser a la même allure même si elle est équiphasée.
|
Les ondes rayonnées par le champ électrostatique justifient la force de Coulomb. Puisqu'on parle ici de mécanique ondulatoire, il faut rappeler que les ondes qui parviennent en phase sur le noyau central de l'électron ou du positron auront pour effet de le repousser, alors qu'il doit se produire plutôt un effet d'attraction si ces ondes parviennent en opposition de phase. Pour être plus précis, un électron emprunte une partie de l'énergie des ondes qui circulent dans l'éther, puis il les rayonne tout autour de lui. Cet emprunt se traduit par un effet d'ombre, mais celui-ci est annulé par la pression de radiation des ondes que l'électron émet. Bref, l'effet d'ombre étant constant, une pression de radiation insuffisante produit un effet d'attraction alors qu'on obtient plutôt un effet de répulsion si elle est plus forte. En première analyse, il est évident que si deux électrons s'éloignent lentement l'un de l'autre, leurs ondes parviendront alternativement en phase, puis en opposition de phase. La pression de radiation sera alternativement supérieure à l'effet d'ombre, puis inférieure, d'où un effet nul. Il est donc impossible de justifier la force de Coulomb uniquement par ces ondes. Il faut plutôt faire appel aux ondes émises par le champ électrostatique. Le propos de cette page sera de démontrer que les ondes rayonnées par le champ électrostatique seront constamment en phase entre deux électrons, ou constamment en opposition de phase entre un électron et un positron. Les diagrammes à période fixe. On a choisi ici de montrer des électrons qui s'éloignent progressivement, mais ce pourrait être l'inverse. Cette méthode exige que la période des électrons soit fixe, bien sûr selon 0 pi, de manière à juger ensuite de la période relative des ondes émises par le champ lorsqu'elles atteignent les électrons, selon différentes distances. Pour cette raison, la période des ondes stationnaires présentes sur le plan central semblera inversée dans les animations, les phases étant dirigées vers le centre. Elles se dirigeraient au contraire vers l'extérieur si les électrons se rapprochaient : |

La période des ondes stationnaires du plan central évolue vers le centre si les électrons s'éloignent.
Mon calcul simplifié n'évalue que ce plan, en présumant que l'ensemble rayonne de la même manière.
|
Le champ électrostatique a une masse selon : E = mc2. On sait depuis Lorentz que si deux électrons sont projetés l'un vers l'autre à 86,6% de la vitesse de la lumière, la masse de chacun d'eux est doublée, soit selon le facteur gamma. Le gain de masse correspond à l'énergie cinétique. Toutefois, à cause de l'effet de répulsion, ils devront éventuellement s'immobiliser et leur masse diminuera de moitié. En vertu de la loi de la conservation de la masse et de l'énergie, la masse et donc l'énergie correspondante ne peut pas se perdre. Je montre à la page sur la masse active et réactive qu'elle est tout simplement stockée dans le champ électrostatique de la manière suivante : |

La masse correspondant à l'énergie cinétique est temporairement stockée dans le champ électrostatique.
Cette énergie est en mesure de propulser de nouveau les deux électrons à 86,6% de la vitesse de la lumière.
Le champ électrostatique constitue donc de la matière : c'est de l'énergie cinétique « en conserve ».
Le champ gluonique présente les mêmes caractéristiques, mais il est beaucoup plus puissant.
|
L'unification des forces. Cette animation montre d'une manière on ne peut plus claire que le champ électrostatique contient de l'énergie. Comme l'électron, il est amplifié par les ondes de l'éther, et il doit donc rayonner des ondes. Ce sont ces ondes qu'il s'agira d'évaluer. De plus, le champ gluonique présente sensiblement les mêmes caractéristiques, ce qui permet d'unifier les forces électrostatiques et la force nucléaire dite forte. Seule, la distance importe. Il est bien évident que si la force électrostatique augmente en raison inverse du carré de la distance, elle atteint des valeurs énormes si cette distance est très courte. Il faut souligner que ces forces résultent de l'addition des ondes émises par les électrons. Or, à très faible distance, de l'ordre de quelques longueurs d'onde, les électrons ne contiennent que des ondes stationnaires. Ils n'émettent pas d'ondes tout près d'eux, ce qui fait que le champ gluonique faiblit brusquement à très courte distance. Ce détail est en accord avec les observations : on s'étonne en effet que la force du champ gluonique croisse au lieu de diminuer lorsqu'on éloigne les quarks l'un de l'autre. C'est aussi ce qui permet aux deux électrons qui forment ces quarks de demeurer à proximité sans être repoussés. La force nucléaire faible résulte plutôt du rayonnement du champ gluonique. Dans tous les cas, si l'on ajoute la gravité, la lumière visible et invisible, la pression par contact étant de nature électrostatique, toutes les forces sans exception sont attribuables à des ondes. Elles sont même toutes attribuables à des champs de force. La tendance actuelle est d'attribuer une particule à toutes ces forces : photons, gravitons, gluons, etc. Soyons clairs, ces particules n'existent pas. Le rayonnement d'un laser. Comme je l'ai mentionné plus haut, le calcul paraxial complet d'un champ électrostatique serait excessivement long, donc impraticable même avec les ordinateurs actuels. Mais tout indique que le résultat sera finalement très semblable au rayonnement que produit un laser, à proximité de la fenêtre d'émission : |
|
|
Le faisceau d'un laser comporte des "points noirs", soit des zones sur l'axe où le rayonnement est nul.
Ces zones alternent avec des points blancs où l'amplitude atteint un maximum.
On reconnaîtra la diffraction de Fresnel.

La courbe mobile indique qu'il se produit une rotation de phase d'un lobe à l'autre.
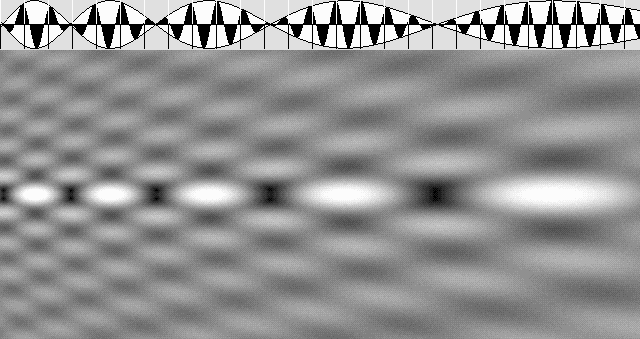
Plus près du laser, les zones sont plus rapprochées.
La partie du haut indique l'amplitude des ondes le long de l'axe, et leur position.
C'est aussi ce que montre l'animation ci-dessous:
![]()
Les traits verticaux sont distants d'une longueur d'onde et ils se déplacent à la vitesse de la lumière.
Remarquer que la période est décalée d'un lobe à l'autre, ce qui produit une inversion de phase.
Étonnamment, les ondes présentes sur l'axe se déplacent plus vite que la lumière.
|
La clé du mystère. Les ondelettes de Huygens parviennent au point à évaluer selon un certain angle, d'où un "effet de ciseau". Leur somme sur un point de l'axe donné produit une augmentation de leur longueur d'onde et aussi de leur vitesse, ce qui fait que leur fréquence effective demeure inchangée. Étrangement, ces ondes se déplacent plus vite que la vitesse de la lumière. C'est une chose bien connue en acoustique, par exemple lorsque vient le temps d'évaluer l'effet de deux haut-parleurs dans un système stéréophonique. Ce qui semble un simple détail sans importance est en réalité la clé du mystère : si les électrons se repoussent, c'est qu'il se produit une inversion de phase au moment où ils passent d'un lobe à l'autre. Au lieu d'alterner comme on pourrait s'y attendre, la période des ondes émises par le champ gluonique demeure constante d'un lobe à l'autre. Le phénomène du point noir est universel. On est ici en présence d'une source émettrice qui n'est pas ponctuelle : elle s'étend sur une certaine surface. J'ai pu constater que dans ce cas, ces zones d'amplitude minimum et maximum étaient présentes quel que soit le phénomène, la seule exception étant l'apodisation (il s'agit de répartir l'énergie de la source selon la distribution normale, ce qui n'est pas le cas ici). On peut donc les retrouver au foyer d'un miroir de télescope, dans le faisceau d'un laser ou d'un sténopé, dans le rayonnement d'un réseau d'antennes ou celui d'un émetteur muni d'un réflecteur parabolique, etc. Elles sont présentes même dans le son qui traverse une ouverture circulaire pratiquée dans un plan, et dont les dimensions sont très supérieures à la longueur d'onde. Il s'agit de ce qu'on appelle la diffraction de Fresnel. Très clairement, parce qu'il constitue lui aussi une source non ponctuelle qui s'étend dans l'espace, le champ électrostatique devrait comporter sur son axe des zones où le rayonnement se renforce ou s'annule périodiquement. Je présume donc que les spécialistes en optique ou en acoustique me suivront au moins jusqu'ici sans sourciller. La série de Balmer s'explique par les points noirs du laser. Je tiens à faire déjà le rapprochement avec la série de Balmer, en la reliant à la périodicité similaire des points noirs du laser, qui se situent très exactement aux distances L correspondant à un multiple entier n pair de la longueur d'onde, en fonction du rayon R de la source rayonnante, selon la série suivante : La série de Fresnel : L = R 2 / (n * lambda) Ces zones d'amplitude nulle ou maximum ont donc un lien avec le nombre de Fresnel, qui est soumis à la même formule. Les points noirs se produisent lorsque n est pair, alors qu'on retrouve les points blancs lorsque n est impair. Par exemple, pour un rayon de 0,5 mm et une longueur d'onde de 0,00065 mm (rouge orangé), le premier point noir (le plus éloigné) du faisceau du laser se situe à 192 mm, soit 0,25 / (2 * 0,00065). Le second est au tiers de cette distance, le troisième au quart, et ainsi de suite. Cette formule indique aussi qu'un sténopé dont le trou fait 1 mm de diamètre produit déjà une image acceptable si sa pseudo-focale fait 454 mm : 0,5 * 0,5 / (1 * 0,00055) avec n = 1. On se demande comment il se fait que les opticiens ne signalent jamais que le sténopé produit une image acceptable pour un nombre de Fresnel égal à 1. C'est la distance minimum, car on réduit beaucoup l'effet de diffusion en respectant la formule suivante, établie selon le chiffre d'Airy et selon le diamètre D du trou : L = D 2 / 2,44 l La pseudo-focale idéale d'un sténopé dont le diamètre du trou fait 1 mm est donc de 745 mm. Si vous voulez le vérifier, de même que la présence des points noirs, souvenez-vous que le faisceau d'un laser peut vous aveugler pour la vie. Il vaut mieux projeter le faisceau d'un laser éloigné à travers un trou circulaire faisant environ cinq millimètres, puis observer les points noirs et les points blancs au moyen d'une feuille de papier en guise d'écran. En vertu du principe de Huygens, ce trou (qui est l'équivalent de celui d'un sténopé) se comporte en effet comme s'il s'agissait lui-même de la fenêtre émettrice d'un autre laser. Je suis toujours sidéré quand j'examine les compte-rendus qui font la démonstration de la diffraction de Fresnel. Tous se perdent dans une mer d'équations différentielles complexes alors que mes programmes d'ordinateur, qui ne font qu'appliquer le principe de Huygens, produisent les mêmes résultats beaucoup plus simplement. En particulier, il n'est plus nécessaire de prendre en compte les conditions aux limites. Ne pourrait-on pas au moins le reconnaître ? De plus, ces compte-rendus ne parlent presque jamais de ces points noirs, alors que ceux-ci sont bien présents et facilement observables. À cause de la nouvelle mécanique ondulatoire, leur importance s'avère capitale pour expliquer la structure des atomes, la constante de Planck et les quanta. Le champ gluonique contient des points noirs équidistants. Dans le cas d'un laser, les points noirs obéissent à la série de Fresnel indiquée plus haut. Mais dans les environs du disque d'Airy qui se forme au foyer d'un miroir de télescope, ils sont régulièrement espacés. Voici une vue longitudinale de ce disque d'Airy, le trait vertical blanc indiquant le plan focal : |
|
|
Les « points noirs » près du foyer d'un télescope sont régulièrement espacés.
|
S'il en est ainsi, c'est parce que les ondelettes de Huygens se renforcent sur une surface sphérique, la fenêtre d'un laser étant au contraire plane. Or ce sont des ondes stationnaires sphériques qui produisent les champs gluoniques. Il en ressort que ces points noirs équidistants à l'intérieur des champs gluoniques peuvent capturer des protons et des neutrons. C'est pour cette raison que les nombreux protons et neutrons d'un atome lourd sont en mesure de se corder les uns près des autres, toujours selon des distances fixes. Tous leurs points noirs coïncident et se renforcent. Tout indique que les neutrons agissent comme des tampons capables d'équilibrer localement la charge électrostatique des protons. Ils contiennent en effet deux quarks "down" qui produisent des champs magnétiques intenses avec les deux quarks "up" du proton et avec son positron, de manière à lier l'ensemble en un noyau très stable. La différence entre ces quarks provient du spin des deux électrons qui les composent, ou du fait que le quark pourrait aussi être fait à la fois d'un positron et d'un électron. On montre à la page sur les champs magnétiques que ceux-ci prennent naissance chaque fois qu'un électron célibataire, c'est à dire sans son semblable du spin opposé, est en présence d'un positron. Pour la même raison, tout électron célibataire dans l'une des couches d'un atome ou d'une molécule produit un champ magnétique. Ce sont donc les points noirs équidistants du champ gluonique qui expliquent la manière dont les protons et les neutrons s'assemblent à l'intérieur d'un noyau d'atome lourd comme celui du plomb. Puisque le proton présente une structure à la fois cubique et octaédrique, le noyau d'un atome lourd devrait respecter la même configuration. Par contre, si les champs gluoniques présentent des points noirs équidistants, ils sont eux-mêmes faits d'ondes stationnaires planes ou presque. Comme le laser, ils rayonnent donc à leur tour des faisceaux d'ondes à l'intérieur desquels d'autres points noirs respectent la série de Fresnel. Le proton rayonne des points noirs. Le phénomène du point noir étant universel, j'affirme donc que le proton, qui contient de nombreux champs gluoniques, devrait également rayonner sur différents axes de telles zones périodiques où le rayonnement est nul. Ces zones ne sont pas équidistantes, et elles baignent dans un rayonnement dont l'intensité varie de la même manière. Ces points noirs sont susceptibles de capturer l'unique électron de l'atome d'hydrogène en différents endroits bien précis, où l'énergie requise pour les en expulser varie selon les multiples d'un nombre entier, donc d'une manière quantique. Cela explique pourquoi l'hydrogène rayonne de la lumière selon les séries de Balmer, Lymann et Paschen. S'il y a de nombreux protons et neutrons, les points noirs coïncident et se renforcent. Le noyau d'un atome lourd peut donc de la même manière capturer de nombreux électrons sur différentes couches atomiques, dont la distance est invariable. S'ils sont expulsés de leur position, ces électrons la réintégreront éventuellement et ils oscilleront jusqu'à stabilisation en émettant des "paquets d'ondes". Il s'agit effectivement de quanta de lumière, dont l'énergie est toujours la même. Mais ce ne sont que des ondes. Très clairement, le photon représente l'énergie d'un quantum de lumière, et non pas une particule. Les ondes stationnaires axiales agissent différemment. Mon raisonnement se fonde sur l'observation suivante : seules, les ondes stationnaires axiales varient de manière significative si les électrons s'éloignent l'un de l'autre. Tout le reste évolue d'une manière linéaire constante et non cyclique. Le rayonnement du champ électrostatique est le résultat de l'addition des ondes provenant du système extérieur stable avec celles provenant du système central cyclique. C'est ce qui explique la présence des points noirs et des points blancs. Le diagramme ci-dessous montre que ces ondes stationnaires axiales affectent la forme d'un cigare très allongé, plus exactement un ellipsoïde : |
|
|
Les ondes stationnaires axiales centrales affectent la forme d'un cigare, c'est à dire un ellipsoïde allongé.
Si la distance des électrons varie, elles évoluent d'une manière cyclique tout en rayonnant comme un laser.
Mais il s'y ajoute ou s'y retranche les ondes provenant de tout le reste, qui est constant.
|
Sachant qu'un laser est également un espace où se forment des ondes stationnaires, la seule différence provient du fait que cet espace est cylindrique et non ellipsoïde. On en conclut que leur diagramme de rayonnement devrait être à peu près similaire. Les ondes stationnaires axiales rayonnent comme un laser. La longueur L du "cigare" varie comme le carré de son rayon maximum R, soit selon : L = R 2, le tout en longueurs d'onde. Il importe de souligner que la tache d'Airy qui se forme au foyer d'un télescope possède elle aussi un longueur. Elle présente en effet un point noir à chaque extrémité, dont la distance correspond également au carré de son rayon mesuré en longueurs d'onde. Une étude plus attentive montre qu'on a plus exactement : L = lambda * (R 2 + 1) L'addition n'est significative que si le rayon mesuré en longueurs d'ondes est très faible, ce qui n'est pas le cas ici. Dès que les électrons s'éloignent l'un de l'autre, la période relative des ondes stationnaires qui se forment sur le plan central évolue en fonction de leur distance. Il faut rappeler que presque toute l'énergie provenant du reste du champ est constamment annulée, parce que les différents anneaux qu'on peut observer sur les animations montrées ci-dessus sont alternativement en phase, puis en opposition de phase. Et en dernier lieu, la distance qui sépare deux électrons vaut normalement des millions de fois leur longueur d'onde. Afin de réduire encore les temps de calcul, il m'a fallu analyser une situation où ces électrons étaient très rapprochés l'un de l'autre, mais en ne tenant compte que des ondes qu'ils émettent. Dans ce cas, la distance entre les points noirs ne mesure que quelques longueurs d'onde, ce qui rend la démonstration plus évidente. C'est donc ainsi que j'ai pu établir que le diagramme de rayonnement paraxial du champ électrostatique devrait avoir cet aspect : |

Le rayonnement du champ électrostatique.
La section de droite montre l'état de l'onde stationnaire centrale, le noir indiquant l'opposition de phase.
Les électrons représentés par les cercles blancs sur les traits noirs s'éloignent lentement l'un de l'autre.
On constate que les zones d'amplitude nulle ou maximum, sur l'axe, se déplacent en sens contraire.
|
Le diagramme strictement axial. Il est beaucoup plus facile de programmer un diagramme qui ne calcule l'amplitude que sur l'axe. Le risque d'erreur est aussi bien moindre, et il est alors possible de comparer les deux résultats. Bien que n'étant pas strictement identiques, le calcul paraxial étant excessivement lent et très imparfait, tous les deux n'en indiquent pas moins que la période des ondes qui parviennent aux électrons ne varie pas. La précision du calcul axial étant bien meilleure, c'est à l'aide de ce programme que le diagramme ci-dessous a été établi. Il montre très clairement que les zones d'amplitude nulle ou maximum se déplacent dans le sens contraire de celui des électrons. Mais il montre surtout que les ondes qui parviennent à l'électron subissent entre chaque zone une rotation de phase d'une demi-onde. Miraculeusement, cette inversion de phase d'une zone à l'autre maintient constamment la période de ces ondes en phase avec celle des deux électrons : |
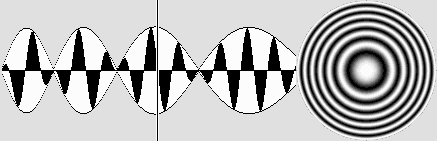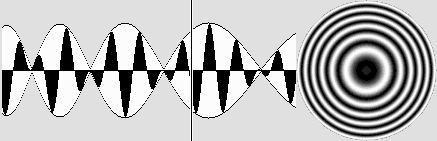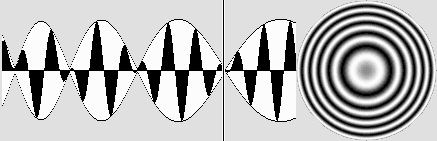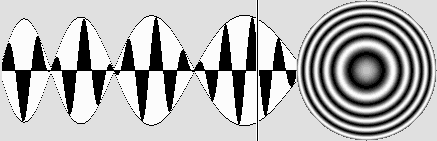
Le trait vertical mobile indique la position de l'électron.
Les ondes qui parviennent à chacun des électrons sont constamment en phase.
À cause de la pression de radiation, ces électrons seront donc constamment repoussés l'un de l'autre.
LES EFFETS D'ATTRACTION
|
Tout effet d'attraction résulte d'une pression en sens opposé. Cette page montre que les variations de la pression de radiation dépendent de la période relative entre les ondes provenant du champ de force et celles des électrons. Il en ressort que la pression de radiation peut varier entre un maximum et une valeur nulle, mais qu'elle n'est jamais négative. S'il se produit un effet d'attraction entre un positron (ou un proton) et un électron, c'est qu'il existe aussi du côté opposé un autre champ de force. Dans un premier temps, il faut remarquer que si deux sources d'ondes émettent à la quadrature, ce qui est le cas d'un positron et d'un électron, on peut obtenir un rayonnement unidirectionnel le long de l'axe : |
|
|
Un électron et un positron produisent un rayonnement asymétrique qui varie selon leur espacement.
Ici, le rayonnement est nul à droite et il atteint un maximum vers à gauche.
C'est dû au fait qu'ils émettent à la quadrature, ce qui est bien connu en radioélectricité.
L'ensemble ne peut produire un champ de force que du côté gauche.
|
Le champ de force plano-convexe composite. Ci-dessus, on constate que le rayonnement unidirectionnel vers la gauche résulte en réalité de la somme des deux rayonnements. Il s'agit d'un rayonnement composite qui se comporte sensiblement comme celui d'un seul électron lorsqu'il se compose avec un rayonnement fait d'ondes planes venant en sens inverse. L'éther est parcouru en effet par des ondes planes, ce qui produit les champs de force plano-convexes : c'est ce qu'on montre à la page sur les champs de force, ou sur la gravité. Il en résulte un champ de force plano-convexe plus complexe : il est composite. Un électron et un positron s'attirent. Selon la mécanique ondulatoire que cette étude propose, les positrons sont en avance ou en retard d'un quart d'onde sur les électrons, ce qui autorise deux spins pour chacun. Il s'ensuit que les ondes stationnaires entre un électron et un positron ne se forment jamais exactement sur le plan central. Elles se situent plutôt à un quart d'onde d'un côté et de l'autre de ce plan central. À cause de l'aller et retour de l'énergie, la période des ondes émises par le champ électrostatique, et qui agissent sur les deux particules, est finalement décalée d'une demi-onde. Ainsi donc, au lieu d'être en phase, ces ondes sont en opposition de phase entre un électron et un positron. Les ondes émises au centre et qui parviennent aux particules sont plus faibles, ce qui signifie qu'un positron et un électron exercent entre eux un effet de répulsion relativement faible. Si ces particules s'attirent, c'est donc parce que les ondes qui circulent en sens contraire exercent une pression de radiation plus intense qui pousse les particules l'une vers l'autre. Ce phénomène est donc sensiblement le même que celui de la gravité. |
| 01 | 02 | 03 | 04 | 05 | 06 | 07 | 08 | 09 | 10 | 11 | 12 | 13 | Vous êtes ici. | 15 | 16 |
| 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 |
|
Gabriel LaFrenière, Bois-des-Filion en Québec. Sur l'Internet depuis septembre 2002. Dernière mise à jour le 12 septembre 2009. La théorie de l'Absolu, © Luc Lafrenière, mai 2000. La matière est faite d'ondes, © Gabriel Lafrenière, juin 2002. |