L'INTERFÉROMÈTRE DE MICHELSON
L'interféromètre de Michelson avant et après contraction.
![]()
![]() Page d'accueil :
La
matière est faite d'ondes.
Page d'accueil :
La
matière est faite d'ondes.
UNE IDÉE GÉNIALE
|
À partir de 1881, Albert A. Michelson a tenté d’évaluer la vitesse de la Terre à travers l’éther à l'aide d'un interféromètre. Mais ce dernier n’a rien révélé. Ce fut un « échec ». En réalité cette expérience a conduit à une découverte scientifique sans précédent, c'est à dire les transformations de Lorentz et la théorie de la Relativité. Aux dires de sa fille, Michelson aurait expliqué à ses enfants qu'un nageur qui traverse une rivière entre deux bornes situées sur les rives opposées gagne plus facilement une course s'il se mesure à un autre nageur qui doit parcourir la même distance dans les deux sens dans la direction du courant.Une course entre deux avions. Si les avions avaient existé à son époque, Michelson aurait sûrement parlé plutôt d'une course entre deux avions. Supposons que le règlement oblige les deux pilotes à parcourir une distance de 100 kilomètres sur un trajet aller et retour. Les deux avions sont identiques et leur vitesse maximum est de 100 kilomètres à l'heure. Mais au moment de prendre le départ, les pilotes constatent que le vent souffle très fort, à 50 kilomètres à l'heure. L'un d'eux décide de prendre le départ dans le sens du vent, espérant prendre une avance insurmontable. Mais l'autre est plus astucieux. Il choisit de faire plutôt le trajet vent de côté et il gagne la course. C'est que ces deux avions se comporteront exactement comme le font les ondes de la lumière. Leur vitesse en l'absence de vent peut être comparée à la vitesse absolue de ces ondes. Mais en présence de vent on peut considérer que c'est plutôt leur référentiel (c'est à dire le sol) qui se déplace comparativement à l'air ambiant, réputé au repos. Alors cet air ambiant peut être comparé à l'éther, qui permet la propagation des ondes de la lumière. D'où un « vent d'éther ». |
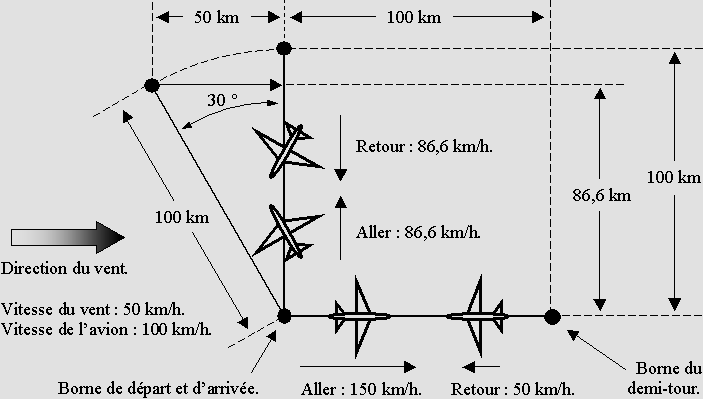
La course entre deux avions.
|
Les calculs de Michelson étaient passablement laborieux. Pour simplifier les choses, Lorentz et Poincaré utilisaient la vitesse normalisée bêta, qui vaut : v/c. C'est bien connu, c indique la vitesse de la lumière, v étant la vitesse d'entraînement. Dans notre exemple, v est plutôt la vitesse du sol en comparaison de l'air ambiant réputé au repos, soit 50 km/h. La vitesse maximum des avions équivaut à c et elle vaut 100 km/h. On a donc ici : bêta = 0,5.On peut alors utiliser la formule suivante, qui indique la vitesse relative V de la lumière, compte tenu d'un angle de propagation j :V = c (cos (arc sin (b sin j) ) – b cos j) Cette formule indique que la vitesse relative V des avions comparée au sol vaut 86,6 km/h en travers du vent, soit 90°. Elle vaut respectivement 50 km/h contre le vent à 0°, et 150 km/h vent derrière à 180°. Elle serait de 58,2 km/h à 45° et de 129 km/h à 135°. On peut faire plus simple. Mais dans le cas de ces avions et de l'interféromètre, il suffit d'évaluer la vitesse relative dans le sens du vent et en travers du vent. Il est alors beaucoup plus simple d'utiliser le facteur de contraction g de Lorentz, qui vaut :
Le facteur gamma de la Relativité correspond à l'inverse du facteur g : gamma = 1 / g. Le facteur g vaut donc ici 0,866. Ce chiffre multiplié par la vitesse maximum de l'avion indique que sa vitesse relative comparée au sol sera réduite à 86,6 km/h s'il vole en travers du vent. Or il faut plutôt utiliser le carré de ce coefficient (soit 0,75) pour obtenir sa vitesse moyenne s'il fait l'aller et retour dans la direction du vent. Cette vitesse moyenne sera donc de 75 km/h : Vitesse moyenne dans la direction du vent : V = g 2 c g 2 = 0,75 V = 75 km / h Vitesse constante en travers du vent : V = g c g = 0,866 V = 86,6 km / h Par ailleurs le pilote qui vole en travers du vent ne peut pas mettre le cap droit devant. Il doit incliner son avion d'un angle thêta valant ici 30° selon : arc sin bêta. Résumons : bêta = v / c bêta = sin thêta bêta = 0,5 g = (1 – bêta 2 ) 1 / 2 g = cos thêta g = 0,866 thêta = arc sin bêta thêta = 30° Par temps calme, les avions parcourent évidemment la distance de 100 km en une heure s'ils volent à 100 km/h. Il leur faudra 2 heures pour faire l'aller et retour peu importe la direction. Mais à cause du vent, il se produit apparemment un ralentissement de leur vitesse si elle est évaluée comparativement au sol. Si l'avion vole en travers du vent, le temps nécessaire pour boucler le trajet aller et retour correspond au coefficient g, alors que c'est selon le carré de ce coefficient s'il vole dans la direction du vent : Sur l'axe : 2 heures / g 2 = 2,6667 heures. En travers : 2 heures / g = 2,3094 heures. Ainsi l'avion qui vole en travers du vent gagnera normalement la course par 0,3573 heure, soit plus de 21 minutes. On voit que la différence est considérable, et elle s'applique également à la vitesse relative des ondes dans un référentiel en mouvement. C'est Michelson qui semble avoir découvert cette anomalie, et c'est ce qui l'a conduit à imaginer et à construire son interféromètre. D'autres petits avions. On montre ci-dessous d'autres petits avions qui effectuent l'aller et retour sur deux axes orthogonaux x et y. La vitesse de ces avions est constante de manière à simuler le comportement d'un front d'onde. Ils vous permettront de visualiser encore mieux ce qui se passe :
En l'absence de vent, les deux avions mettent le même temps pour parcourir la même distance.
Mais ici, le vent souffle par le travers à la moitié de la vitesse des avions (bêta = 0,5). À gauche, on a le trajet apparent alors qu'à droite, il s'agit plutôt du trajet réel. Il est clair que la longueur absolue du trajet est augmentée selon : Cos(thêta) = 0,866 thêta = ArcSin(bêta) = 30 ° bêta = Sin(thêta) = 0,5 Or le cosinus de l'angle thêta correspond au facteur de contraction g de Lorentz : g = Sqr(1 – bêta ^ 2) = Cos(30°) = 0,866
Ici, le vent souffle dans la même direction que celle des avions. Dans ce cas, la longueur du trajet est augmentée selon g au carré.
La transformation de Michelson. On peut donc considérer que cette transformation des ondes selon Michelson se nomme la transformation de Michelson. On y reviendra à la page sur les transformations de Lorentz. Elle implique une contraction même sur les axes y et z : x' = x * g ^ 2 + t * bêta t' = t – x * bêta y' = y * g z' = z * g La transformation des coordonnées selon Michelson respecte les mêmes proportions que celle de Lorentz, mais elle est plus sévère. Elle correspond au point où il ne devrait se produire aucun ralentissement de la fréquence des ondes, et donc des horloges, pour des raisons mécaniques. Par contre, à cause de l'effet Doppler, qui a une incidence majeure sur la procédure de réglage des horloges, le décalage horaire et plus important encore que dans les transformations de Lorentz. En effet, si la distance entre les bornes montrées ci-dessus était contractée de cette manière, les avions effectueraient toujours leur parcours en deux heures exactement peu importe la vitesse ou la direction du vent. On note toutefois que ces avions, s'ils étaient faits d'ondes stationnaires, devraient être eux-mêmes réduits en taille même sur l'axe transversal, d'où une anomalie que les transformations de Lorentz corrigeront. Contrairement à ce qu'on a toujours prétendu, la transformation de Galilée implique un ralentissement des horloges car elle ne prévoit aucune contraction. Ce ralentissement surviendrait pour des raisons mécaniques et il ne serait pas le même selon qu'il se produirait sur l'axe du déplacement ou sur un angle transversal. Très clairement, la transformation de Galilée est erronée. C'est une chose que même Descartes aurait pu remarquer, puisqu'il a découvert l'existence de l'éther et la nature ondulatoire de la lumière. C'est pourquoi son système de coordonnées à trois dimensions doit être au repos dans l'éther s'il faut évaluer le parcours de la lumière. Une course entre des ondes. La lumière réagissant selon la transformation qu'il avait découverte, Michelson en a déduit qu'il était possible de détecter le vent d'éther au moyen d'un interféromètre. Il imaginait deux ondes de lumière qui devaient faire des trajets identiques, l'un sur l'axe du vent d'éther et l'autre en travers. Le croquis ci-dessous illustre ce dispositif : |
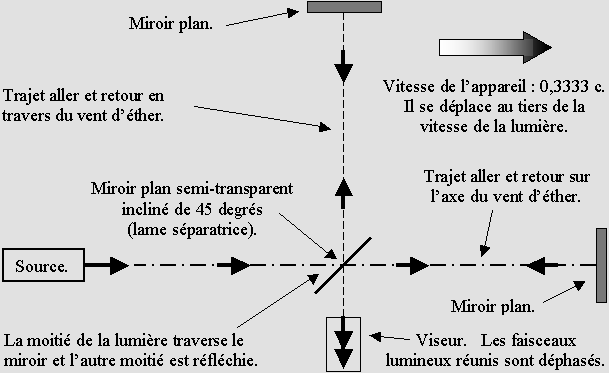
L'interféromètre de Michelson.
|
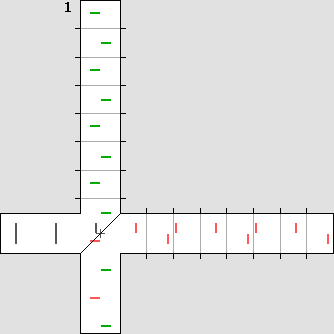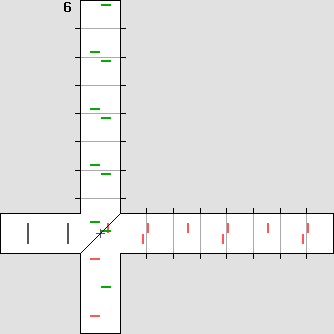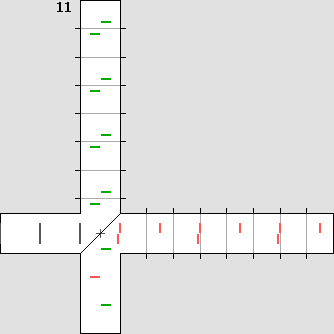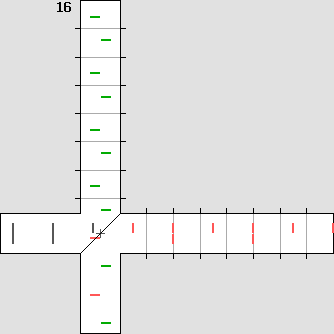
La source émet de la lumière vers la droite, face au vent d'éther. Une lame séparatrice en réfléchit une moitié vers le haut, le reste continuant en ligne droite. Chaque couloir se termine par un miroir plan, où la lumière fait demi-tour. Au retour, la lumière est de nouveau réfléchie ou transmise au niveau de la lame séparatrice. Finalement, les deux faisceaux sont réunis au bas de l'appareil, ce qui permet de comparer la différence de marche des différents plans d'onde. En effet, il se produit alors des interférences additives ou soustractives selon que ces plans d'ondes sont en phase ou en opposition de phase. Michelson notait d'abord la position des interférences, prévoyant constater un décalage après avoir fait pivoter son appareil de 90°. Celui-ci était monté sur une grande dalle de pierre flottant sur un bain de mercure, de manière à éliminer les vibrations nuisibles. La température était soigneusement contrôlée pour éviter toute dilatation de l'appareil. Ignorant tout de sa vitesse absolue, il avait prévu le pire, soit la vitesse de la Terre autour du Soleil : 29 km/s. L'interféromètre de Michelson, en version animée. Pour que la différence devienne perceptible dans une animation, il faut que la vitesse du référentiel soit considérable. On a choisi ici le tiers de la vitesse de la lumière. On remarquera que cette vitesse produit sur l'axe des ondes dont la longueur est deux fois plus grande dans un sens que dans l'autre, le rapport R des longueurs d'onde valant 1 : 2. En effet on a ici : bêta = 0,3333 avec : g = 0,9428 et ce rapport vaut : R = (1 + bêta) / (1 – bêta) Ce rapport indique que de nombreux avions décollant à chaque minute et qui feraient le trajet sur l'axe d'un vent soufflant au tiers de leur vitesse seraient deux fois plus espacés s'ils volaient dans le sens du vent qu'en sens contraire. On peut donc considérer que chaque trait montré dans l'animation ci-dessous représente un avion, les traits en noir représentant deux avions volant côte à côte. Le vent souffle vers la gauche. De plus, sur un axe transversal, les ondes sont comprimées par effet Doppler selon le coefficient de contraction g Lorentz, qui vaut 0,9428 : lambda ' = g * lambda Ci-dessous, à gauche, l'ordinateur affiche exactement la même distance pour les deux bras de l'interféromètre. Cette distance a été calculée de manière à obtenir une différence de marche d'une demi-longueur d'onde, selon la formule indiquée plus bas. Les plans d'onde (ou les avions) sont représentés par des lignes mobiles, qui sont colorées en vert ou en rouge pour distinguer leur cheminement. L'animation de gauche montre ce que Michelson s'attendait de constater : |


L'interféromètre de Michelson avant et après contraction.
|
L'animation de droite montre plutôt ce qui s'est passé en réalité, ce qu'il n'avait pas prévu. L'interféromètre s'est contracté sur l'axe du déplacement (ici, le bras horizontal) selon le coefficient de contraction g de Lorentz, qui vaut 0,9428. La longueur de ce bras a donc été réduite à 94,28 % de sa longueur originale. Alors la différence de marche fut annulée et les ondes se sont retrouvées parfaitement en phase à l'arrivée. Le fait de faire pivoter l'appareil de 90° n'a rien modifié car c'est l'autre bras qui s'est contracté. C'est pour cette raison que l'interféromètre n'a pas pu détecter le vent d'éther.
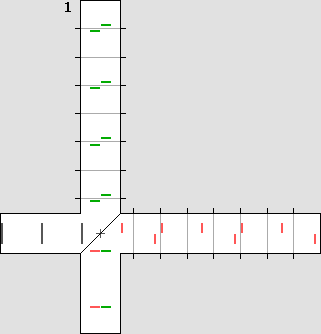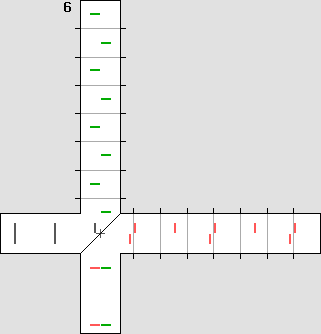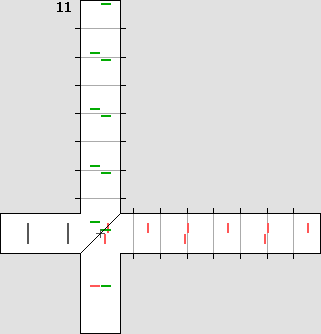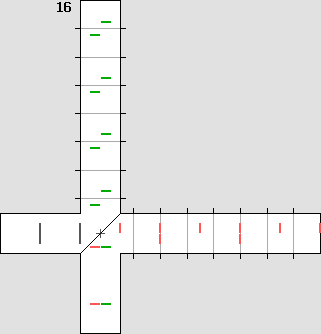
Un fait nouveau. Ces pages montrent que l'éther existe et que la matière est faite d'ondes stationnaires, qui se contractent dans un référentiel mobile. Elles apportent donc une explication, un fait nouveau : la cause de la contraction prévue par Lorentz. Il faut rappeler ici que Michelson croyait à l'existence de l'éther. La présente description de son interféromètre correspond donc très certainement à sa pensée. Toutefois ce n'est pas ce que la communauté scientifique actuelle pense, parce qu'elle a abandonné - à tort - l'hypothèse de l'existence de l'éther. Le lecteur est donc prié de noter que le reste de cette page ne correspond pas à l'opinion générale. Il existe néanmoins à l'heure actuelle une effervescence des idées, sans doute à cause de l'Internet. Ceux qui ont pris la peine de revoir eux-mêmes le cheminement de Lorentz et de Poincaré ont généralement tendance à penser qu'il doit exister un référentiel privilégié, présumé au repos. Ceux qui n'ont pas fait cette vérification devraient se taire, puisqu'ils ne savent pas de quoi ils parlent. L'explication de Lorentz est exacte. Les transformations de Lorentz, c'est donc d'abord et avant tout la contraction des distances, qui se fait uniquement sur l'axe du déplacement x. Prenons comme exemple une vitesse de 0,866 c. Alors on a : bêta = 0,866 et le coefficient de Lorentz g vaut : 0,5. Le facteur gamma vaut 2, soit 1 / g. L'animation ci-dessous montre de manière spectaculaire que si les distances sont contractées de moitié sur l'axe du déplacement, des avions en présence de vent ou encore les ondes de la lumière mettront exactement le même temps pour faire un aller et retour entre une borne centrale et quatre bornes placées sur les axes x et y. Ce dispositif peut donc être vu comme un interféromètre à quatre bras, et la très grande vitesse permet d'illustrer de manière non équivoque que la contraction annule effectivement la différence de vitesse relative : |
|
|
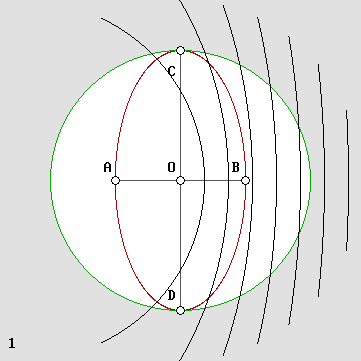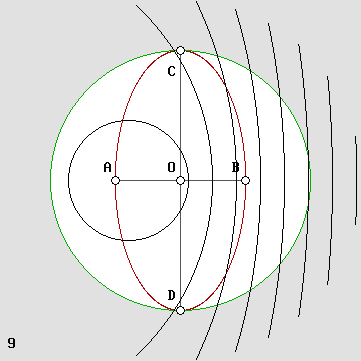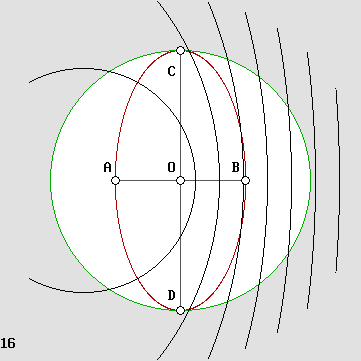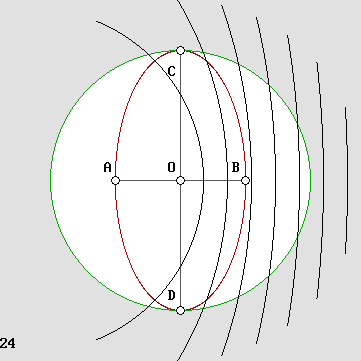
Un interféromètre à quatre bras.
Même si la vitesse est de 0,866 c, les quatre échos reviennent simultanément à la source.
L'interféromètre à 20 bras de M. Philippe Delmotte, qui a réalisé lui-même l'animation (cliquez sur l'image).
Grâce à l'Éther Virtuel, nous pouvons vérifier que des échos radar tous azimuts reviennent ensemble à la source.
Ce médium virtuel étant un véritable laboratoire, les résultats peuvent difficilement être contestés.
L'effet Doppler.
|
Pour cette raison, un observateur central qui tenterait de connaître la distance des bornes A, B, C et D montrées ci-dessus à l'aide d'un signal radar, trouverait que ces bornes sont à égale distance. Toutefois on remarquera que le temps nécessaire pour boucler le circuit serait doublé, selon le facteur gamma. La matière étant faite d'ondes, tous ses mécanismes en sont ralentis de la même manière, d'où un ralentissement de sa vitesse d'évolution. D'un point de vue mathématique, on parle d'une dilatation du temps. Mais le temps n'étant qu'un concept, il ne peut posséder une telle propriété. Entendons-nous, ce sont plutôt les horloges qui ralentissent. Ici, elles avanceront d'une demi-seconde, soit selon le facteur g, pendant qu'une horloge au repos avance d'une seconde. Une référence absolue. L'animation ci-dessus montre très clairement que l'observateur O est en mesure de connaître la distance absolue qui le sépare de C ou de D, parce que dans tous les cas la différence de vitesse relative des ondes sur un axe transversal est réduite de la même manière que le temps qu'il mesure selon ses horloges. Par exemple, si cette distance est d'une seconde lumière du point de vue d'un observateur au repos, dont les observations sont absolues, il mesurera également une seconde lumière. Contrairement à Michelson, nous disposons maintenant d'un atout considérable, car nous savons que la distance entre les nœuds des ondes stationnaires sur un axe transversal est invariable. Cela indique que les distances mesurées sur cet axe sont toujours exactes, peu importe la vitesse. Il s'agit d'une référence absolue. On verra plus loin que cela permet d'éliminer l'un des deux bras de l'interféromètre. C'est bien évidemment inutile puisque celui-ci ne peut toujours pas détecter le vent d'éther. Mais ce qui est souverainement satisfaisant, c'est qu'il s'agit d'un argument décisif et dévastateur contre l'initiative de Kennedy et Thorndyke, qui ont utilisé un interféromètre dont la longueur des bras n'était pas la même. Ils en ont conclu que l'éther n'existait pas. Mais leurs calculs étaient erronés car ils n'ont pas tenu compte des effets temporels des transformations de Lorentz. Le secret des transformations de Lorentz. On montre ci-dessous que les ondes stationnaires se contractent selon le facteur de contraction g de Lorentz au carré sur l'axe du déplacement, et selon le facteur g seulement sur les axes perpendiculaires. Si les ondes stationnaires qui constituent la matière ne se contractent que sur l'axe du déplacement, et seulement selon ce facteur g, c'est parce que leur longueur d'onde augmente simultanément (leur fréquence ralentit) selon la réciproque de ce même coefficient, soit : 1 / g . De plus les avions montrés plus haut atteignent plus rapidement la borne s'ils ont le vent derrière. Henri Poincaré a montré qu'un observateur qui veut synchroniser sa montre sur celle d'un autre placé plus loin sur l'axe x doit le faire par signaux optiques (ou par radio, découverte à cette époque). Il en résulte forcément un décalage horaire, mais l'observateur est incapable de s'en rendre compte. Dans un référentiel qui se déplace à travers l'éther, il existe donc ce que Poincaré a appelé des heures locales. Elles conduisent à une « simultanéité virtuelle » qui permet à la matière de continuer de fonctionner normalement, d'une manière mécanique qu'on pourra désormais expliquer. Et en dernier lieu, les ondes qui se contractent par effet Doppler accumulent de l'énergie, et l'on sait que l'énergie de la matière équivaut à sa masse. C'est ainsi que j'ai pu mettre en évidence des facteurs d'action et de réaction qui rendent compte de l'augmentation de masse de la matière selon l'effet Doppler. Voilà donc le secret des transformations de Lorentz : tout s'explique si la matière est faite d'ondes. Il aura fallu 100 ans pour percer ce mystère. C'était pourtant évident, car Lorentz et Poincaré en ont établi les valeurs à partir des transformations de Voigt, qui visaient à neutraliser l'effet Doppler. Elles ont donc un lien direct avec l'effet Doppler et avec les ondes. La contraction des ondes stationnaires. On aura remarqué dans l'animation de l'interféromètre de Michelson montrée plus haut qu'il s'y produit des ondes stationnaires, ce qu'on ne mentionne jamais. Pour les mettre en évidence, l'emplacement des nœuds a été souligné par des repères. On observe qu'il se produit aussi des ondes stationnaires même sur l'axe du déplacement malgré l'effet Doppler, qui fait en sorte que la longueur d'onde est doublée au retour. Avec un peu de concentration on peut observer que les ondes croisent quand même simultanément les repères parce que celles dont la longueur est doublée semblent se déplacer deux fois plus vite. Ce phénomène est peu connu et il est montré à la page sur les ondes stationnaires. On peut parler alors d'ondes pseudo-stationnaires ou d'ondes "stationnaires mobiles", dont on montre deux exemples ci-dessous. Par ailleurs le temps que mettent les ondes pour effectuer un trajet aller et retour peut être évalué selon le même calcul qui a été utilisé plus haut pour déterminer lequel des deux avions gagnerait la course. En ramenant la vitesse de la lumière c à l'unité, on obtient : Vitesse relative moyenne des ondes sur l'axe x : 1 / g 2 Vitesse en travers : 1 / g Contraction des onde stationnaires sur l'axe x : g 2 Contraction en travers : g On note que la contraction des ondes stationnaires correspond à la réciproque de la vitesse relative des ondes progressives. On voit bien que les deux options donnent les mêmes résultats. Ceci montre que Michelson aurait pu fonder plutôt ses calculs sur la contraction des ondes stationnaires. En fait, c'est même nécessaire car Lorentz et Poincaré ont corrigé les calculs de Michelson. On peut désormais se baser sur le fait que la contraction en travers est annulée à cause du ralentissement de la fréquence, ce qui fait que la distance entre les nœuds des ondes stationnaires sur un axe transversal est invariable : il s'agit d'une constante absolue. |
LA CONTRACTION DES ONDES STATIONNAIRES

Les ondes stationnaires normales, dans un référentiel au repos. bêta = 0
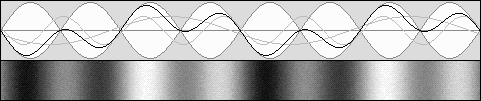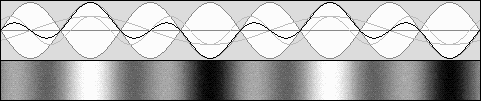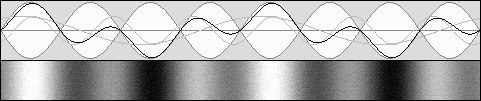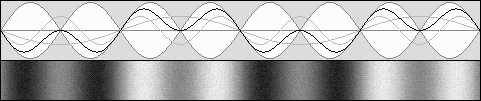
Les ondes stationnaires mobiles : bêta = 0,5 g = 0,866 Contraction de 0,75 selon g 2.
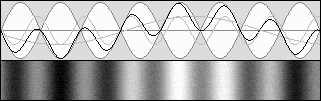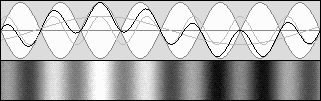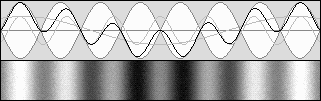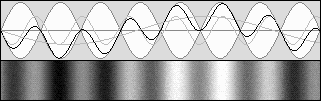
bêta = 0,707 g = 0,707 Contraction de 0,5 selon g 2.
|
Enfin, une explication vraisemblable. Dès 1892, l'Irlandais George F. FitzGerald a émis l'hypothèse que l'interféromètre devait se contracter en présence du vent d'éther. Il a même tenté de l'expliquer en présumant que la matière subissait la pression de ce vent. Lorentz et Poincaré ont repris cette hypothèse en y incorporant les effets temporels, mais sans grande conviction. FitzGerald et Lorentz ignoraient tout des propriétés ondulatoires de la matière, mais c'est une chose connue depuis Louis de Broglie. Dès ce moment on aurait pu relever la concordance entre la contraction Lorentz-FitzGerald et la contraction des ondes stationnaires. Aujourd'hui cette étude va plus loin encore en affirmant que la matière est faite exclusivement d'ondes stationnaires. Dans ces conditions, l'interféromètre doit se contracter de la même manière que les ondes stationnaires montrées ci-dessus. C'est évident : il est fait lui-même d'ondes stationnaires. En 1904, Hendrik A. Lorentz a donné la valeur exacte de la contraction. Elle se fait selon le facteur g sur l'axe du déplacement seulement. Ils ont montré qu'elle devait aussi provoquer un ralentissement des horloges, de la fréquence des ondes, etc. Il s'ensuit un décalage horaire. C'est ce qu'on appelle les transformations de Lorentz.
|
|
C'est pour cette raison que l'interféromètre de Michelson s'est contracté selon le coefficient de Lorentz g, et uniquement sur l'axe de son déplacement x. |
![]()
LE CALCUL DE LA LONGUEUR DES BRAS DE L'INTERFÉROMÈTRE.
|
On aura constaté dans les animations montrées plus haut qu'il faut un peu plus de 4 longueurs d'ondes pour obtenir l'opposition de phase lorsque la vitesse vaut le tiers de celle de la lumière. Cette distance est plus grande si la vitesse du référentiel est plus faible, et c'est pourquoi l'interféromètre de Michelson était très grand. De plus il comportait de nombreux miroirs pour augmenter encore la durée du trajet. Certains ont poussé la précision jusqu'à tenir compte du fait qu'un miroir réfléchit les ondes en opposition de phase, mais en pratique c'est inutile parce que le nombre de réflexions est pair. La période finale est donc intacte. Il faut aussi préciser que l'épaisseur de la lame séparatrice provoque une aberration qu'il faut corriger à l'aide d'une lame compensatrice. Michelson considérait uniquement la différence de vitesse des ondes et ses calculs était passablement laborieux. Comme on l'a répété plus haut, Lorentz et Poincaré ont corrigé ses calculs, ce qui permet d'établir que les mesures de distance effectuées sur tout axe transversal sont absolues. On peut avantageusement se référer plutôt à la compression des ondes stationnaires plutôt qu'à la vitesse. Selon le cas, il faut donc d'utiliser les formules suivantes, qui permettent de calculer la longueur L des deux bras qui provoquera l'opposition de phase : Selon la longueur d'onde d'origine : L = g * lambda / 4 ( 1 – g ) Selon la longueur d'onde mesurée dans le référentiel : L = lambda / 4 ( 1 – g ) Il faut insister sur le fait que selon la première formule la longueur d'onde est mesurée dans un référentiel au repos. C'est celle qu'il a fallu utiliser au moment de programmer, au moyen de l'ordinateur, les animations montrées plus haut. Mais Michelson devait plutôt utiliser la deuxième, puisqu'il se déplaçait déjà. C'était, rappelons-le, dans l'espoir de détecter la vitesse absolue de la Terre à travers l'éther, en supposant que la matière ne se transforme pas selon Lorentz. Bien évidemment, Michelson ignorait que la fréquence de la lampe de son interféromètre variait en fonction de la vitesse. On pourra vérifier toutefois que la différence est minime si la vitesse présumée n'est que de 29 km/s. Il faut composer avec des ondes et des mesures transformées. D'une part les ondes sont comprimées selon g sur un axe transversal, mais d'autre part la fréquence a ralenti également selon g de manière à allonger la longueur d'onde selon 1 / g. En définitive la longueur d'onde sur cet axe ne varie jamais. De plus, selon Lorentz, il n'y a pas de contraction sur un axe transversal et les mesures de longueur effectuées sur cet axe sont toujours invariables et absolues.Sur l'axe du déplacement, la longueur d'onde est comprimée selon g 2 mais on a vu ci-dessus qu'elle est également dilatée selon 1 / g. En définitive elle est seulement comprimée selon g. Le
problème se résume donc à comparer la longueur d'onde invariable sur
un axe transversal avec la longueur d'onde contractée selon g sur l'axe
du déplacement.
Un exemple. Prenons
comme exemple une contraction de 10%. On a alors g = 0,9 et
bêta = Si la contraction est de 10%, il faut 5 demi-longueurs
d'onde pour obtenir l'opposition de phase.
Le pire des scénarios. On sait
aujourd'hui que le Soleil voyage à une vitesse de
300 km/s environ comparativement aux galaxies environnantes. On peut
raisonnablement penser que cette vitesse pourrait être sa vitesse absolue.
Elle pourrait même être très supérieure. Si l'on choisit cette vitesse,
bêta vaut : 300 / 300000, soit
0,001, et le
coefficient de contraction g vaut 0,9999995. La formule donne alors 500000
longueurs d'ondes, chacune valant environ 0,0006 mm. La longueur des bras de l'interféromètre devrait
donc être de 30 cm seulement à cette vitesse.
Mais
Michelson a préféré jouer prudemment en envisageant le pire des scénarios,
soit la vitesse de la Terre autour du Soleil, qui est de 29 km/s. Cela
suppose que le Soleil soit parfaitement au repos dans l'éther, ce qui
est très improbable, et même statistiquement impossible. Il a donc dû construire un interféromètre
énorme, malgré l'addition de nombreux miroirs. En effet on obtient
alors les valeurs suivantes :
On a : 1 / 4 (1 – g) soit 53 419 000 fois la longueur d'onde, donc 32 000 mm. Ainsi la longueur des bras de l'interféromètre doit être idéalement de 32 mètres pour détecter une vitesse aussi faible que 29 km/s. En 1887, la longueur du trajet des rayons dans l'expérience Michelson-Morley était de 11 mètres, ce qui aurait été suffisant pour détecter des variations significatives. En 1902, Morley a essayé de nouveau en portant cette distance à 32 mètres, toujours sans résultats. |
![]()
L'EXPÉRIENCE KENNEDY-THORNDYKE ÉTAIT ABERRANTE.
|
L'interféromètre de Michelson était inutilement complexe. Sauf erreur, personne n'a jamais signalé le fait que l'un de ses deux bras était superflu. Ce bras peut être raccourci et réduit à un miroir plan placé près de la lame séparatrice : |
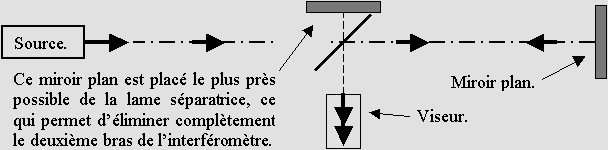
L'interféromètre de Michelson simplifié.
|
On obtient finalement l'équivalent d'une cavité Fabry-Pérot, ce que l'interféromètre Tama du Japon met à profit malgré la présence des deux bras perpendiculaires qui est maintenue pour d'autres raisons. Cette configuration n'est pas évidente si l'on considère son fonctionnement comme s'il s'agissait d'une course, car alors ce ne sont plus du tout les ondes d'origine que l'on compare. Mais puisqu'il s'agit en réalité d'ondes stationnaires, et malgré les nombreux miroirs, on peut considérer que leur contraction ou leur dilatation dans un seul des deux bras aurait pu tout aussi bien révéler le vent d'éther. Idéalement, il faudrait alors utiliser des ondes planes. En effet les deux taches d'Airy d'un laser étant sphériques à courte distance, ils n'auraient plus le même rayon de courbure vu la différence dans la longueur des trajets.Quelque
soit sa longueur, le bras le plus court
sert uniquement de référence, car la comparaison immédiate ne peut
rien révéler. Ce n'est pas comme lors d'une course d'avions, car il est
impossible de distinguer les plans d'onde successifs. On ne peut tout de
même pas affecter un numéro à chacune des ondes. On ne peut
détecter que leur décalage. Il faut réaliser que c'est uniquement après avoir fait pivoter leur
interféromètre d'un quart de tour, et à plusieurs reprises selon
différents angles et différentes heures du jour (compte tenu du plan
de l'écliptique), que Michelson et Morley s'attendaient de constater un
changement dans la position des interférences.
Il
faut en conclure que l'expérience Kennedy-Thorndyke, bien qu'elle
ait confirmé ces résultats avec une grande précision, était
aberrante.
Selon de nombreux compte-rendus, ses concepteurs prétendaient que le fait d'utiliser deux bras
dont la longueur n'était pas la même devait révéler le vent d'éther
même advenant une contraction de l'interféromètre. Certains en ont
conclu à
tort que l'éther n'existait pas. L'éther existe. Or
c'est tout à fait faux. Toute différence dans la longueur des bras aurait dû effectivement produire des résultats différents si la contraction
selon Lorentz n'avait pas eu lieu. Mais puisque cette contraction a
lieu, elle annule toute variation. À l'évidence, les ondes stationnaires
qui constituent la matière dont
l'interféromètre est fait se comportent exactement de la même manière que les ondes
stationnaires formées par la lumière qui circule entre ses miroirs. Tout
indique que cette erreur s'est produite parce qu'on a négligé de
prendre en compte le ralentissement de la fréquence selon la vitesse.
En effet les transformations de Lorentz font état d'une contraction, mais
elles prévoient également un ralentissement de la fréquence de
la lumière, et donc une augmentation de sa longueur d'onde. En
utilisant la méthode qui se réfère à la contraction des ondes
stationnaires, on se rend compte que, dans ces conditions, la longueur
d'onde de la lumière sur un axe transversal ne varie jamais. C'est
qu'en fonction de la vitesse, la longueur d'onde absolue augmente selon
1 / g alors qu'elle diminue sur cet axe selon g à cause de l'effet
Doppler.
On a finalement :
lambda ' = |
![]()
L'aberration angulaire.
|
On a parfois objecté que si l'interféromètre se contracte, l'angle de son miroir oblique ne peut plus se maintenir à 45°. Alors il ne pourrait plus réfléchir la lumière selon un angle de 90° selon la loi bien connue en optique des miroirs, qui stipule que l'angle du rayon réfléchi est égal à l'angle du rayon incident. Mais dans un référentiel qui se déplace, cette loi devient inexacte. C'est d'ailleurs Lorentz lui-même qui a signalé l'aberration angulaire qui en résulte à Michelson, avant même d'avoir établi ses célèbres transformations. Il avait sans doute appliqué le principe de Huygens, qui explique la lumière par des ondelettes. Le principe de Huygens. D'ailleurs la présente étude explique effectivement la lumière par de telles ondelettes, qui sont donc bien réelles. Ce que je vais dire ici n'est pas vraiment pertinent et vous semblera certainement suspect, mais j'affirme qu'un miroir est incapable de réfléchir la lumière, qui est faite d'ondes. Ce sont les électrons présents sur la surface de ce miroir qui émettent de nouvelles ondelettes en opposition de phase dans toutes les directions. Celles qui sont émises vers l'arrière annulent la lumière qui a traversé, d'où une ombre. Celles qui sont émises sur la surface du miroir constituent ce qui semble être la lumière réfléchie, mais qui est en fait de la toute nouvelle lumière. Il est évident que ces ondelettes doivent subir l'effet Doppler si elles sont émises à grande vitesse, d'où une distorsion. Lorentz craignait pour sa part qu'une déviation anormale ne vienne fausser les calculs de Michelson. Beaucoup de textes confondent cette aberration avec l'aberration des étoiles de Bradley, mais celle-ci ne se produit que s'il existe une différence de vitesse entre la source lumineuse et le récepteur. Or la source et le récepteur se déplacent à la même vitesse dans l'interféromètre. On montre à la deuxième page sur la Relativité de Lorentz que l'aberration des étoiles n'est jamais perceptible à cause du décalage horaire. Mais à cette époque Lorentz l'ignorait. Une étude minutieuse du comportement des ondelettes révèle que l'angle du rayon réfléchi correspond toujours exactement à 90° quelle que soit la vitesse de l'interféromètre, donc quelle que soit l'angle du miroir consécutif à la contraction. L'animation ci-dessous montre que cette aberration est annulée exactement parce que les ondes réfléchies dans une direction perpendiculaire doivent être inclinées selon l'angle thêta = arc sin v / c. Pour que cet angle concorde, il faut corriger l'angle du miroir, et ce nouvel angle correspond précisément à la contraction prévue par Lorentz : |
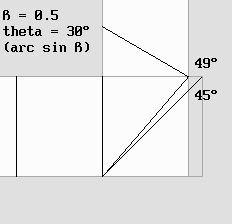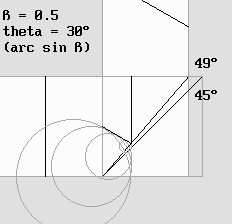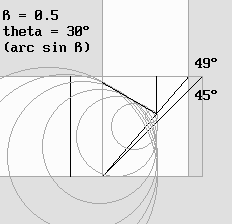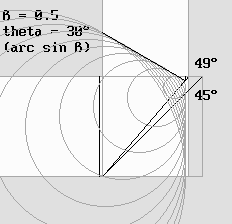
Si l'interféromètre se contracte, l'angle de la lame séparatrice en est modifié.
|
L'appareil se déplace vers la droite à la moitié de la vitesse de la lumière. On a : bêta = 0,5. Dans ce cas la vitesse relative des ondes qui se déplacent vers la droite (dans le sens du déplacement du miroir) vaut 0,5 c selon: 1 – bêta. La vitesse relative des ondes qui se déplacent vers le haut (donc en travers du vent d'éther) correspond au coefficient de contraction g de Lorentz, qui vaut ici 0,866.Le miroir de la lame séparatrice doit être incliné d'un angle valant arc tan (1 / g) = 49,1° de manière à respecter la contraction de l'appareil. D'un autre côté, après réflexion sur le miroir, l'onde doit impérativement être inclinée selon l'angle thêta , qui vaut 30°. L'animation montre qu'en appliquant le principe de Huygens, cette condition est respectée.On constate que les ondelettes sphériques suivent les ondes planes parce que leur centre de courbure est au repos dans l'éther. L'addition de milliards d'ondelettes qui prennent naissance à tour de rôle sur la surface de la lame séparatrice provoque la formation d'une onde plane unique, exactement comme le prévoyait Huygens. La merveilleuse harmonie des transformations de Lorentz apparaît alors dans toute sa splendeur. De nouvelles preuves. Depuis que nous disposons d'un médium virtuel informatique, à voir à la page sur l'éther, le vent tourne en faveur de la Relativité de Lorentz. Je répète que ce dernier croyait fermement à l'existence de l'éther, ce qui ne l'a pas empêché de mettre au point la Relativité en étroite collaboration avec Poincaré. Voici deux diagrammes produits par mon programme Ether19.exe Ether19.bas :
Ces deux systèmes se déplacent vers la droite à la moitié de la vitesse de la lumière. À gauche, le faisceau convergent est dévié par une lame séparatrice inclinée selon Lorentz. À droite, l'angle de la lame a été maintenu à 45° exactement. Voici l'animation AVI correspondante produite par ce même programme Ether19 : http://glafreniere.com/avi/Michelson_transversal.avi
Il est clair que si l'angle de la lame séparatrice demeure à 45° quelle que soit la vitesse de l'interféromètre, le faisceau lumineux ne sera plus réfléchi sur un plan orthogonal. Or si l'interféromètre se contracte comme le prévoyait Lorentz, le plan des ondes réfléchies demeure parfaitement perpendiculaire à l'axe du déplacement : le faisceau lumineux sera réfléchi sur cet axe. Vous pouvez aussi télécharger les deux animations indiquées ci-dessous pour observer comment la diffraction de Fresnel se comporte en présence de la lame séparatrice. Elles ont été réalisées à l'aide de ce même programme Ether19. J'ai pris la peine d'y insérer les quatre orientations possibles de l'interféromètre. On observe que dans tous les cas, le faisceau lumineux est bien réfléchi comme le prévoyait Lorentz : ether19_axial_petit.wmv ether19_transversal_petit.wmv Il s'agit ici d'une première. Cette démonstration n'avait jamais été faite, et elle est manifestement en faveur de Lorentz. Ne vous y trompez pas : cette expérience est au moins aussi importante que celle de Michelson. Elle montre en particulier que les ondes qui se propagent par le travers sont systématiquement inclinées : thêta = arc sin (v / c). Par exemple, à la moitié de la vitesse de la lumière, les ondes transversales sont inclinées de 30°. L'angle atteint 45° à 0,707 c. De plus, la lame séparatrice a pour effet de contracter le faisceau lumineux selon les prévisions de Lorentz ou de rétablir sa largeur originale, selon le cas. La structure même de la tache d'Airy ou de la diffraction de Fresnel se comporte également comme le prévoyait Lorentz, c'est à dire qu'on observe une contraction sur l'axe du déplacement. Bref, cette expérience montre que l'interféromètre de Michelson se contracte, mais que son opérateur est incapable de s'en rendre compte. Depuis la rédaction de cette page, j'ai réalisé de meilleures animations encore à propos de l'interféromètre de Michelson. Elles sont vraiment spectaculaires, et les résultats sont bien évidemment en faveur de Lorentz. Les voici : Michelson_Interferometer.5c.mkv Michelson_Interferometer.7c.mkv Michelson_Interferometer_Stationary.mkv Michelson_Interferometer_No_Contraction.mkv Voici
le programme FreeBasic que
j'ai écrit pour obtenir ces images
: Un argument spectaculaire et pourtant méconnu. Il ne s'agit donc pas d'une objection. Il s'agit plutôt d'une confirmation spectaculaire que les transformations de Lorentz ont réellement lieu, en fonction de la vitesse absolue de la matière comparativement à l'éther. D'une part l'interféromètre de Michelson se contracte, ce qui annule la différence de vitesse des ondes. D'autre part l'angle de la lame séparatrice est modifié de manière à corriger l'aberration angulaire, ce qui permet aux deux faisceaux lumineux de se rejoindre exactement au même endroit. L'appareil ne peut rien détecter. Des centaines d'auteurs, souvent parmi les plus "respectables", affirment sans sourciller que cette expérience a permis de démontrer que l'éther n'existait pas. Ces gens sont des moutons de Panurge, les pires qui soient. Ils croient aveuglément tout ce qu'on leur raconte au lieu de douter de tout et de tout vérifier selon le conseil de Descartes : « Dubium sapientiae initium » : l'intelligence (ou la sagesse) repose sur le doute. |
![]()
Lorentz avait raison.
|
Ainsi donc, l'interféromètre de Michelson s'est vraiment contracté comme FitzGerald, Larmor et Lorentz l'ont d'abord affirmé. Il s'agissait d'une hypothèse simple et vraisemblable, et pourtant personne ne les a cru. Tous ont préféré se rallier à la théorie de la Relativité d'Albert Einstein, même si elle faisait appel à une transformation de l'espace-temps tout à fait déraisonnable. Cette approche exclusivement relativiste fut une erreur monumentale. Il aurait fallu sauvegarder à tout prix le point de vue absolu. |
|
Il aurait fallu évaluer plus attentivement comment un observateur en mouvement devrait percevoir les choses, en considérant que l'éther existe et que la matière se transforme réellement comme Lorentz l'a montré. |
|
La Relativité est donc remarquablement simple. Ce n'est pas une théorie mystérieuse qui dépasse l'entendement. C'est une loi de la nature qui peut se vérifier au moyen de calculs élémentaires. On en fait la démonstration à la page sur les transformations de Lorentz. Elle est étayée par des démonstrations similaires à la page sur la Relativité de Lorentz. La différence essentielle avec le concept erroné d'Einstein, c'est qu'on peut montrer que tout observateur en mouvement est toujours victime d'une mystification. Seul, un observateur au repos absolu voit les choses telles qu'elles se sont produites. Mais parce que celui qui se déplace a lui aussi l'impression d'être au repos, il a l'impression que c'est plutôt celui qui est au repos qui se déplace et qui subit les transformations de Lorentz. Dans ces conditions aucun d'eux ne peut savoir avec certitude lequel des deux se déplace vraiment. En plus clair, la différence essentielle, c'est que l'un a tort et que l'autre a raison. La Relativité d'Einstein prétend que les deux ont raison. Elle confond les apparences et la réalité. En revanche, non seulement la Relativité de Lorentz se vérifie, mais on peut l'expliquer, ce qui est un avantage considérable. C'est même une véritable révolution. Il faut donc réhabiliter l'éther, qu'on a banni injustement, et qui s'avère essentiel. La matière se transforme selon les prévisions de Lorentz. Les pages dont la liste figure plus bas ont ceci de très particulier qu'elles sont fondées sur une explication mécanique de la matière et de tous les phénomènes physiques. Il ne s'agit pas seulement d'une théorie qu'on pourra vérifier un jour, il s'agit de faits qu'on peut confirmer dès maintenant. Quoi qu'il en soit, il n'existe à l'heure actuelle qu'une seule explication logique :
La conclusion qu'il faut en tirer s'impose : la matière s'assemble et fonctionne à l'aide d'ondes stationnaires, d'une manière mécanique. Si elle se déplace, ces ondes subissent l'effet Doppler. C'est pourquoi elle doit se transformer comme Lorentz l'a montré. Ce n'est pas une hypothèse, c'est une évidence. |
| 01 | 02 | 03 | 04 | 05 | 06 | Vous êtes ici. | 08 | 09 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 |
|
Gabriel LaFrenière, Bois-des-Filion en Québec. Dernière mise à jour le 09-09-09. Sur l'Internet depuis septembre 2002. Courrier électronique : veuillez consulter cet avis. La théorie de l'Absolu, © Luc Lafrenière, mai 2000. La matière est faite d'ondes, © Gabriel Lafrenière, juin 2002. |