LES TRANSFORMATIONS DE LORENTZ
Cette page a été entièrement refaite en janvier 2011.
|
La Relativité n'est pas un phénomène qui dépasse l'entendement.
Mais pour la comprendre, il faut d'abord bien connaître les effets des transformations de Lorentz.
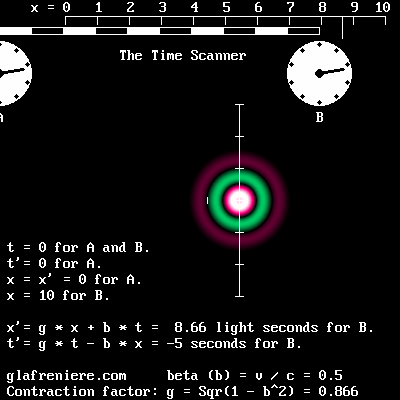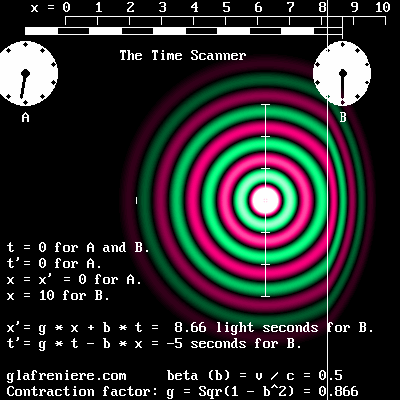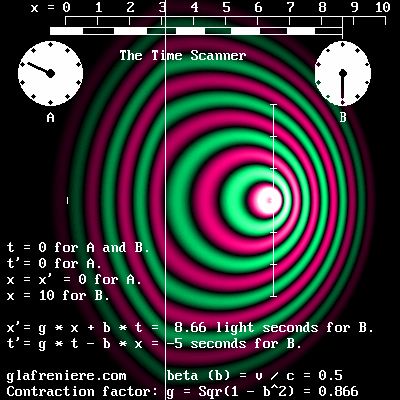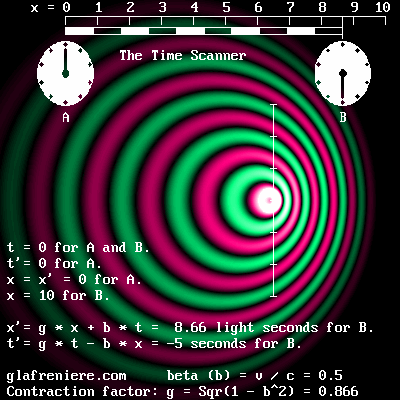
Le « Scanner du Temps » reproduit les mêmes effets spatiaux-temporels typiques de l'effet Doppler.
![]()
![]() Page d'accueil : La
matière est faite d'ondes.
Page d'accueil : La
matière est faite d'ondes.
|
Les équations de Lorentz. Vers 1887, Hendrik Antoon Lorentz (1853–1928) s'intéressait de près aux recherches de Michelson. À cette époque, bien évidemment, son but n'était pas de mettre au point la théorie de la Relativité. Il tentait beaucoup plus simplement d'expliquer pourquoi l'interféromètre de Michelson n'avait pas détecté le mouvement absolu de la Terre comparativement à l'éther. Il avait fait valoir dès 1895 que n'importe quelle contraction de cet appareil, pourvu qu'elle soit conforme à ses équations préliminaires, était susceptible d'annuler la différence de vitesse de la lumière sur deux axes orthogonaux en raison de l'effet Doppler. Il avait aussi remarqué dès cette époque qu'une telle contraction devait entraîner des effets temporels. Puisqu'il existait tout un éventail de possibilités, Lorentz cherchait donc à déterminer quelle contraction et quels effets temporels convenaient le mieux pour annuler parfaitement ce qu'on appelait à l'époque "l'aberration". Dans ces pages, cette fameuse aberration est assimilée au facteur de contraction de Lorentz, qu'on représentera par la lettre "g". Je suis d'avis qu'on aurait dû combler cette carence vraiment ennuyeuse il y a longtemps. En effet, dès qu'on parle de la Relativité, on parle systématiquement d'une contraction. Or le célèbre "facteur gamma" qui figure dans les équations de Poincaré semble indiquer plutôt une dilatation puisqu'il est toujours supérieur à l'unité. Le facteur de contraction correspondra donc à l'inverse du facteur gamma. Sa valeur s'obtient plus facilement si l'on adopte une vitesse normalisée à la manière de Poincaré, appelée ici bêta.
Lorentz et Poincaré ont travaillé sur ce problème pendant plus de dix ans. Ils ont considéré les champs électromagnétiques au voisinage d'un électron en mouvement; ils ont vérifié plus exactement les diverses valeurs de contraction et de temps qui auraient pour résultat d'immobiliser parfaitement cet électron. Henri Poincaré parlait de "l'impossibilité de mettre en évidence le mouvement absolu". Dans son livre "Électricité et Optique", publié en 1901, il mentionne que Lorentz avait déjà trouvé que la constante de Voigt "l" de ses équations préliminaires devait être égale à 1. En 1904, Lorentz publia sa version définitive qui, il faut bien le dire, diffère de celle montrée ci-dessous, en particulier en ce qui concerne l'équation du temps. Elle comportait toujours la constante de Voigt devenue inutile. Il en ressort que les "transformations de Lorentz" telles qu'on les connaît aujourd'hui correspondent plutôt à la version donnée par Henri Poincaré en 1905, mais dont la constante de Voigt a été supprimée.
Les transformations de Lorentz. Il vaut mieux inverser ces équations. Ci-dessus, la variable x' concerne l'électron au repos. Puisque ce détail important pour la suite des choses est rarement mentionné, j'ai mis ci-dessous un extrait du célèbre mémoire de Poincaré publié en 1905. C'est au paragraphe 6.
C'est très clair : Poincaré remplace l'électron en mouvement par un électron immobile. Il applique donc la variable x' à l'électron immobile, ce qui prête à confusion. Dans cette étude, les équations proposées seront donc toujours inversées de manière à ce que la variable x désigne plus justement l'électron au repos. C'était d'ailleurs ce que proposait Poincaré en 1901. Vous verrez que ces "transformations transformées" deviennent alors bien plus limpides. Un obstacle inutile : les équations de Maxwell. Si vous avez la patience de parcourir attentivement les écrits de Lorentz, de Larmor et de Poincaré, vous verrez que la quasi-totalité de leurs démonstrations exigent une connaissance approfondie des équations de Maxwell. Or ces équations font intervenir de nombreux concepts que peu de gens sont en mesure de maîtriser. Par exemple, malgré toute leur science, MM. Rigal et Henry, les auteurs d'un livre sur la radioélectricité générale publié en 1959, reconnaissent qu'il est "plus prudent de laisser le dernier mot aux résultats expérimentaux"! D'ailleurs, vers 1920, Lorentz lui-même faisait remarquer qu'on pouvait trouver moins de vingt physiciens dans le monde capables de comprendre la Relativité. Et aujourd'hui, plus personne ne s'y retrouve. De l'aveu même de Lorentz, ses transformations étaient très semblables à celles de Woldemar Voigt, elles aussi applicables en principe aux équations de Maxwell. Pourtant, le but de Voigt était plus simplement d'annuler l'effet Doppler. Il faut donc insister sur le fait que, bien que ni Lorentz ni Poincaré ne le mentionnent clairement, c'est d'abord et avant tout de l'effet Doppler qu'il s'agit. Les transformations de Voigt reproduisent d'ailleurs parfaitement les ondes sonores, qui n'ont absolument rien à voir avec les équations de Maxwell. Voici un programme qui le montre sans l'ombre d'un doute. Doppler_Voigt_transformations.bas Doppler_Voigt_transformations.exe On gardera donc à l'esprit qu'ici, on a affaire à des ondes et à l'effet Doppler. Or il s'agit de phénomènes relativement simples qu'on peut peut fort bien traiter sans devoir recourir aux équations de Maxwell, qui constituent un obstacle majeur et inutile qu'il vaut beaucoup mieux éviter. Le facteur de contraction de Lorentz g et la vitesse normalisée bêta. Je répète que dans ces pages, la lettre "g" représente le facteur de contraction de Lorenz, grandeur que Poincaré appelait "l'aberration". Il s'agit de l'inverse du facteur gamma, qu'on ignorera parce qu'il conduit à des équations plus difficiles à interpréter. Ainsi donc, le facteur g remplace avantageusement l'encombrant: racine(1–v^2/c^2) qu'on retrouve dans les transformations de Lorentz montrées plus haut. De plus, toujours par souci de simplicité, il vaut mieux adopter une vitesse normalisée, une autre trouvaille de Poincaré. On a ici: bêta = v / c. Dans ce cas, on a: c = 1, en remarquant que la vitesse de la lumière au carré demeure alors 1. Grâce à ces mesures élémentaires, les équations inversées que je propose ci-dessous sont bien plus simples. Mais on y gagne surtout parce que tous les effets concrets des transformations de Lorentz y sont clairement exprimés. Il se produit quatre transformations distinctes, d'où l'emploi du pluriel. Deux d'entre elles s'appliquent aux mesures de l'espace et deux autres aux mesures du temps.
Les transformations de Lorentz inversées et simplifiées.
Je tiens à rappeler que les hypothèses les plus simples sont les plus vraisemblables. Or ici, on pourrait difficilement faire plus simple. D'une part, la matière en mouvement, contractée selon: x' = g * x à l'instant t = 0, se sera déplacée ensuite d'une distance additionnelle égale à: bêta * t. D'autre part, la période des ondes ralentit selon: g * t et il se produit un décalage horaire ou une onde de phase correspondant à: –bêta * t. Si vous ne voyez pas le lien avec les transformations de Lorentz montrées plus haut, la première étape pour le vérifier consiste à extraire la variable x de la partie droite de la première équation montrée ci-dessus. Alors le facteur g passe au dénominateur et il représente la grandeur: racine(1 – (v ^ 2 / c ^ 2)). x = (x' – bêta * t) / g Deuxièmement, il faut remplacer la vitesse normalisée bêta par la vitesse v. La multiplication v * t demeure correcte à la condition que les mesures de vitesse et les grandeurs x et x', normalisées ici en secondes-lumière, soient reconverties au système MKS. x = (x' – v * t) / g Et en troisième lieu, on a déjà souligné que la variable x devrait plus logiquement représenter le système au repos. Il faut donc interchanger les variables x et x'. Par contre, il faut éviter d'interchanger les variables t et t', même si à première vue ce serait la bonne chose à faire. Voigt avait donc confondu les variables t et t', erreur que ni Lorentz ni Poincaré n'ont remarquée par la suite puisque n'importe quelle valeur de t est arbitraire. La symétrie fonctionne de toutes façons si l'on n'effectue qu'un seul calcul; par contre, on constate que l'effet Doppler qui résulte d'un grand nombre de calculs effectués pixel par pixel n'est pas reproduit correctement. Ainsi, x' réintègre sa position initiale à la gauche de l'équation :
On retrouve l'équation originale des transformations de Lorentz, dans sa version simplifiée. C'est l'équivalent de la version donnée par Poincaré, sachant qu'on a : gamma = 1 / g. x' = gamma * (x – bêta * t)
L'éther. Les transformations de Lorentz s'appliquent aux ondes dès que le mouvement intervient. On verra plus loin qu'à l'aide de ces équations, on peut facilement montrer des ondes qui subissent l'effet Doppler sur l'écran d'un ordinateur. Mais il importe de savoir exactement à quoi on a affaire en évaluant les variables x, x', t, et t'. Dans cette page, on fera toujours appel à un système de coordonnées cartésien et euclidien présumé au repos dans l'éther. On ne parlera donc jamais d'un "référentiel galiléen". Et enfin, il ne sera surtout pas question de "transformer l'espace-temps", ce qui est proprement absurde. J'insiste sur le fait que Lorentz croyait à l'existence de l'éther lorsqu'il a élaboré ses équations. En outre, c'était certainement un très grand physicien. Dans cette optique, si l'on considère que personne n'a jamais démontré que l'éther n'existe pas, on peut dire que l'attitude catégorique et irrévocable des physiciens de notre époque à propos de l'éther est pour le moins étrange. Après tout, on parle ici des transformations de Lorentz. Elles devraient être d'abord et avant tout examinées et vérifiées en postulant que l'éther existe, c'est à dire selon le concept original de Lorentz. Autrement, il faudrait leur trouver un autre nom et une autre utilité. Malheureusement, incapable d'expliquer la contraction de la matière (une "étrange propriété" qui a tout l'air d'un "coup de pouce" commodément donné par la nature, comme le faisait remarquer Poincaré), Lorentz a changé d'idée par la suite. Mais fort heureusement, nous avons constaté depuis ce temps que la matière présentait des propriétés ondulatoires. Plus récemment, M. Ivanov a découvert que les "ondes stationnaires animées" subissaient une contraction. C'est pourquoi la contraction de la matière en mouvement s'avère maintenant justifiée et facilement explicable. Il ne s'agit plus d'un coup de pouce qui interviendrait comme un Deus ex machina, c'est à dire un fait inattendu et improbable, qui ne suit aucune logique et qui vient fort à propos résoudre un problème autrement insoluble. Lorentz n'a jamais abandonné l'hypothèse d'un éther capable de transmettre la lumière et les ondes radio. En 1920, il écrivait:
Il est clair que Lorentz n'aurait pas pu élaborer ses équations sans effectuer des calculs préliminaires basés sur l'existence de l'éther. Poincaré de son côté mentionnait que "cette hypothèse est commode pour l'explication des phénomènes." Einstein lui-même parlait encore de l'éther après 1920. Si donc vous affirmez qu'il n'existe pas, vous allez un peu vite. Après tout, on aurait dû d'abord expliquer clairement comment la lumière et les ondes radio se propagent avant d'y renoncer. En effet, le fonctionnement mécanique des champs magnétiques et électriques, tout comme leur nature véritable, demeurent toujours un mystère. Quoi qu'il en soit, vous devriez à tout le moins examiner la version "alpha" des transformations de Lorentz proposée ci-dessous puisqu'elle exige la présence d'un médium capable de véhiculer les ondes. Elle s'applique à un phénomène découvert par M. Yuri Ivanov en 1981, et qu'il a appelé les "ondes stationnaires animées". Ce sera le point de départ d'un cheminement qui nous conduira tout droit à la Relativité. On peut facilement reproduire expérimentalement les ondes d'Ivanov. Le point important, c'est qu'on peut en vérifier le comportement à l'aide des ondes sonores, qui ont bien évidemment besoin d'un médium, l'air en particulier, pour se propager. J'ose espérer que vous n'allez tout de même pas prétendre que l'air n'existe pas !... Les transformations de Lorentz s'appliquent à trois phénomènes distincts. Pendant des années, je me suis demandé quelle était la cause fondamentale des transformations de Lorentz. À cause des équations de Voigt, il était évident qu'on avait affaire à l'effet Doppler. Mais ce n'est que récemment, en 2010, que j'ai découvert que ces transformations s'appliquaient différemment à trois phénomènes distincts: 1– Les ondes stationnaires d'Ivanov (transformations alpha). 2 – L'électron (transformations bêta). 3 – La matière (transformations gamma). Mais étonnamment, les équations requises demeurent identiques, de sorte qu'il faut plutôt redéfinir les variables x, y, z et t pour les adapter à chacun de ces trois phénomènes. Vous verrez que cette approche permet d'expliquer beaucoup mieux les transformations de Lorentz. C'est certainement parce qu'il n'avait pas identifié leurs fonctions dans leur ensemble que Lorentz n'a pas réagi plus énergiquement au dérapage de Poincaré. On sait que ce dernier fut le premier à utiliser le terme de "Relativité", mais en postulant vers la fin de sa vie que la contraction de la matière n'était pas réelle et que les phénomènes optiques étaient relatifs. C'est ce qui l'a conduit au désastre final: dans un tel contexte, l'éther devient apparemment superflu puisqu'on n'a plus à s'en préoccuper. Poincaré a donc modifié radicalement la théorie de Lorentz, et c'est finalement Einstein qui l'a supplanté après s'être emparé de ses idées. Je tiens à rappeler que mon Scanner du Temps reproduit à merveille ces trois transformations. Il peut même le faire simultanément. Il réussit ce tour de force parce qu'il balaie une image animée à la vitesse de "l'onde de phase". Ce phénomène découvert par Louis de Broglie apparaît en effet chaque fois qu'on applique les transformations de Lorentz. Il affecte normalement la phase des ondes, qui évolue d'une manière surprenante sur l'axe du déplacement. Mais dans le cas de la matière, l'onde de phase se traduit plutôt par un décalage horaire. Grandmercé, Sèrgi. Je tiens à remercier chaleureusement M. Sèrgi Blanchard, dont les connaissances en mathématiques et en astrophysique m’ont permis d’y voir plus clair. C’est surtout son flair exceptionnel qui a fait toute la différence. Cet homme-là peut repérer juste à l’odeur les failles d’un raisonnement. Même dans la noirceur la plus totale, il est capable de pressentir la direction à suivre. Quoi qu'il en soit, ce fut presque toujours à la suite de ses observations que j’ai réussi à aplanir les difficultés. Depuis un bon moment, de sa lointaine Occitanie, il surveille attentivement ma progression à travers cet incroyable bourbier que constitue la physique actuelle. Sans lui, je dois dire que cette grande aventure aurait été autrement pénible et sans doute beaucoup moins fructueuse.
1 – LES TRANSFORMATIONS ALPHA (s'appliquent aux ondes d'Ivanov). Les ondes que M. Yuri Ivanov avait nommées lively standing waves, c'est à dire "ondes stationnaires animées", se caractérisent par un déplacement des ventres et des nœuds selon une vitesse normalisée que j'appellerai ici "alpha". C'est pourquoi ces ondes transportent l'énergie qu'elles contiennent à cette même vitesse. Il se produit aussi une contraction des ventres, de sorte que les nœuds se rapprochent les uns des autres à mesure que la vitesse alpha augmente. Ces ondes présentent enfin la fameuse onde de phase qui a été décrite pour la première fois par Louis de Broglie. La vitesse de cette onde de phase vaut l'inverse de la vitesse alpha, soit: 1 / alpha. Elle est donc toujours supérieure à la vitesse des ondes, qui peut être celle du son ou celle de la lumière, cette dernière correspondant effectivement à la moyenne géométrique entre la "vitesse de groupe" et la vitesse de phase comme de Broglie l'avait aussi montré. On peut considérer qu'il s'agit d'ondes planes circulant théoriquement en sens opposé, mais dont la longueur diffère. M. Ivanov en a étudié et décrit méthodiquement le comportement vers 1980. Je vous présente donc ci-après les "ondes d'Ivanov".
Les ondes d'Ivanov présentent trois propriétés remarquables : 1 – Les ventres et les nœuds se déplacent à la vitesse alpha. 2 – Les ventres, montrés en blanc, se contractent selon le facteur de contraction g de Lorentz. 3 – Il se produit une onde de phase, bien visible ici sous la forme de franges sombres qui se déplacent vers la droite.
Tout ceci est fondamental : c'est la base même des transformations de Lorentz, et donc de la Relativité. De plus, ces ondes n'étant vraiment pas "stationnaires", il fallait leur attribuer un nom plus pertinent. Je propose qu'elles portent désormais le nom de M. Ivanov, qui est l'auteur de cette découverte. Ce grand chercheur avait pressenti dès le début qu'il touchait là à quelque chose d'important. Il avait montré que la matière elle-même doit se contracter de la même manière que "ses" ondes. Il avait toutefois abouti à des transformations qui ne conviennent qu'aux phénomènes acoustiques, comme on le verra plus loin. Voici donc les équations des transformations alpha, qu'on peut identifier à cause du recours à la vitesse normalisée "alpha".
Les transformations alpha. Il s'agit bien des transformations de Lorentz, mais les variables doivent être interprétées autrement.
Ces équations permettent de reproduire fidèlement les ondes d'Ivanov, comme le programme qui a produit la vidéo proposée ci-dessous le prouve indiscutablement. Standing_Waves_03_Transformations.mkv Standing_Waves_03_Transformations.bas Je rappelle que j'ai dû redéfinir la vitesse alpha en l'attribuant spécifiquement au déplacement des ventres et des nœuds des ondes d'Ivanov. Le facteur de contraction de Lorentz g peut être établi selon cette vitesse: g = racine(1 – alpha^2). Mais il peut tout aussi bien être établi selon le rapport des moyennes arithmétique et géométrique des deux longueurs d'onde en cause. Les équations : y' = y; z' = z sont ici superflues puisqu'on considère des ondes planes. Elles sont toutefois nécessaires s'il faut reproduire les "ondes stationnaires transversales animées" montrées plus bas. Tout est dans la définition des variables x et t. C'est surtout dans la définition et le pré-calcul des variables x et t que la différence d'avec la version de Lorentz est la plus significative. Dans le cas des transformations alpha, les variables x et t font référence à une longueur d'onde établie arbitrairement selon la moyenne géométrique des deux longueurs d'onde impliquées. On aurait pu tout aussi bien choisir la moyenne arithmétique, car le rapport de la moyenne géométrique sur la moyenne arithmétique correspond étonnamment au facteur de contraction de Lorentz g. Mais puisqu'il faut choisir, nous retiendrons la moyenne géométrique. C'est d'abord pour faire plus simple, car il suffit ensuite de faire intervenir le facteur g et non pas son carré. Mais c'est surtout dans le but d'uniformiser les équations pour qu'elles conviennent aux trois transformations alpha, bêta et gamma. On peut obtenir la vitesse alpha à partir du rapport "R" de ces deux longueurs d'onde: R = lambda' / lambda alpha = (R – 1) / (R + 1) Je rappelle que ce calcul se vérifie aussi bien en acoustique qu'en optique. Après tout, on ne fait qu'évaluer deux ondes dont la longueur diffère puisqu'il n'y a pas d'autre variable. Ce n'est pas bien compliqué, et pourtant il aura fallu attendre 1970 pour que M. Ivanov s'y intéresse. Malheureusement, ce dernier a retenu le carré du facteur g pour établir ses propres transformations. On peut en effet recourir au carré pour obtenir l'effet Doppler ordinaire, celui du son par exemple. Il s'agit en pratique d'un cas particulier des transformations de Voigt où la constante de Voigt serait égale au facteur g et non pas à 1 comme dans la version de Lorentz. Par contre, les "transformations d'Ivanov" ne peuvent pas s'appliquer à l'électron, dont la fréquence diminue avec la vitesse... D'ailleurs, en 1895, Lorentz lui-même avait fait la même erreur qu'Ivanov en considérant (entre autres) le carré du facteur de contraction. Il avait heureusement corrigé très vite par la suite. Poincaré précise même que Lorentz y est arrivé avant lui en procédant "par tâtonnements", lui-même ayant par la suite confirmé le choix de Lorentz en invoquant le principe de moindre action (c. f. Maupertuis, Euler, Lagrange). Six courtes séquences vidéo. Voici des vidéos qui montrent divers aspects des ondes d'Ivanov :
Les ondes d'Ivanov reproduites grâce au médium virtuel Delmotte-Marcotte : Standing_Waves_01_Ivanov.mkv On compare plus simplement avec l'addition mathématique des ondes : Standing_Waves_02_Theoretical.mkv Les ondes d'Ivanov sont reproduites grâce aux transformations alpha : Standing_Waves_03_Transformations.mkv Le test de Hertz dans un repère en mouvement (médium Delmotte-Marcotte) : Standing_Waves_04_Hertz.mkv Le test de Hertz effectué à la vitesse alpha. Un émetteur est fixe, l'autre avance à la vitesse bêta : Standing_Waves_05_Alpha.mkv Les ondes d'Ivanov, selon que l'effet Doppler est acoustique ou relativiste : Standing_Waves_06_Doppler.mkv
On aura vu plus haut que la troisième séquence et le programme correspondant (Standing_Waves_03_Transformations.bas) prouvent sans l'ombre d'un doute que les transformations alpha appliquées aux ondes d'Ivanov produisent exactement les mêmes résultats que le médium virtuel Delmotte-Marcotte. Puisque ces transformations correspondent aux transformations de Lorentz mais qu'elles sont appliquées dans un tout autre contexte (et avec autant de bonheur!), ces transformations alpha s'avèrent hautement pertinentes. J'ai donc pris la peine de les exposer d'une manière plus systématique dans le tableau suivant :
Les transformations alpha. Elles ne s'appliquent qu'aux ondes d'Ivanov, qu'elles soient acoustiques ou optiques. Les variables x représentent les distances établies d'après la moyenne géométrique des deux longueurs d'onde. Les variables t représentent la période en radians aux points x et x', là aussi en se basant sur cette moyenne géométrique. Ce sont les mêmes mesures d'espace et de temps qu'on applique partout. Ici, il n'y a pas de Relativité : tout est absolu !
Ci-dessous, j'insiste sur l'aspect géométrique de ces transformations hautement euclidiennes, pythagoriciennes et cartésiennes. Pour éviter un autre dérapage comme celui qui a conduit à une Relativité non euclidienne et franchement surréaliste, il faut réaliser qu'on a affaire tout simplement au théorème de Pythagore. La longueur de l'hypoténuse est normalisée à 1. Elle correspond à la vitesse de la lumière, comme Poincaré l'avait si bien établi en normalisant la vitesse bêta selon v/c. On aura donc c = 1. La longueur des deux côtés adjacents correspond alors au facteur g et à la vitesse alpha. Mais si l'on établit plutôt la longueur de l'hypoténuse selon la moyenne arithmétique des deux longueurs d'onde, le côté où se situait le facteur g correspondra à leur moyenne géométrique. C'est tout à fait remarquable !
Dans cet exemple, les deux ondes considérées mesurent respectivement 50 et 150 pixels. Les variables x doivent être exprimées en longueurs d'ondes établies d'après la moyenne géométrique des deux longueurs d'onde, soit 86,6 pixels. Les équations alpha donnent alors les coordonnées x' correctes. Elles donnent aussi la phase t' correcte en ce point (et non pas le "temps", bien qu'à l'heure actuelle on utilise effectivement la période d'oscillation de certains phénomènes particulièrement stables pour établir l'heure). Si donc on a t = 0 au départ, on peut plus simplement obtenir x' et t' de la manière suivante: x ' = g * x. t ' = – alpha * x. La première formule indique que toute structure faite d'ondes stationnaires se contracte selon le facteur de contraction g. La deuxième indique qu'il se produit une onde de phase. Il s'agit bien de celle que Louis de Broglie a décrite. Comment afficher les ondes d'Ivanov. Il ne faut pas perdre de vue qu'il s'agit ici de reproduire les ondes d'Ivanov sur l'écran de l'ordinateur, dont les coordonnées réelles sont exprimées en pixels. Supposons qu'il s'agit d'en obtenir une seule image, et non pas une animation. Les coordonnées x représentent la distance de l'origine exprimée en longueurs d'onde. On a 86,6 pixels lorsque x = 1. Une distance de 100 pixels correspond donc à x = 1,1547 selon: 100 / lambda. Cette distance indique alors la période t comparativement à celle de l'origine, au point x = 0 où l'on a toujours: t = 0. À ce stade, on a tout simplement: t = x puisqu'il n'y a pas de coordonnées y. Pour ceux qui ne l'auraient pas encore réalisé, on est donc loin ici du "temps" que cette variable était censée représenter dans les transformations de Lorentz. Pour chaque pixel, on aura besoin d'une variable x et d'une variable t. Il faut donc recourir à deux tableaux de variables à une seule dimension. Si l'on souhaite afficher ces ondes fictives de 86,6 pixels avant qu'elles ne subissent les transformations alpha, il faut convertir cette période t en radians. x = distance en pixels / lambda en pixels t = x radian = 2 * pi * t Au point x = 100 pixels, on obtient : radian = 1,1547 * 2 * pi = 7,255. L'amplitude de l'onde en ce point vaut donc sin(radian) = 0,826 alors qu'elle vaut zéro au point x = 0 et 1 au point x = lambda / 4 (quadrature). Puisqu'on a affaire à des ondes planes, il suffit de répéter les mêmes amplitudes verticalement sur une bande d'une certaine largeur, disons 50 pixels. Il faut refaire le même calcul pixel par pixel. S'il y en a 1000, par exemple, cela produira une bande de 50 x 1000 pixels. Pour ma part, j'aime bien représenter les ondes en noir si l'amplitude est à zéro et en blanc si elle atteint un maximum, mais en passant par le vert émeraude (vert et 50% de bleu) et le rouge fuchsia (rouge et 50% de bleu) selon que l'amplitude est positive ou négative. On évite ainsi les dominantes jaunes désagréables, et le comportement des ondes est bien plus facile à interpréter. Ensuite, pour afficher les ondes d'Ivanov , il faut bien évidemment avoir recours aux transformations alpha. x ' = 0,866 * x + 0,5 * t t ' = 0,866 * t – 0,5 * x Finalement, il suffit de convertir les variables x' en pixels et les variables t' en radians : pixel à traiter : x ' * lambda radian = 2 * pi * t ' amplitude = sin(radian) Pour obtenir une animation des ondes d'Ivanov comme je l'ai fait plus haut, il faut augmenter progressivement toutes les grandeurs t selon un pas fixe valant une fraction quelconque de 1, par exemple: 1 / 48. La période générale augmentera ainsi progressivement de manière à atteindre une pulsation de plus pour toutes les variables t lorsque les ondes auront parcouru 86,6 pixels, et cela se produira à la 48ième image. Les transformations alpha reproduisent tout aussi bien les ondes stationnaires transversales. On aura vu à la page sur les ondes d'Ivanov que dans un système en mouvement, les ondes qui se propagent apparemment en sens contraire le long d'un axe transversal y ou z doivent être inclinées d'un angle thêta = arc sin(alpha) de manière à rattraper constamment ce système. Dans ce cas, leur longueur est la même dans les deux sens et il n'est donc plus nécessaire de recourir à leur moyenne géométrique. Par contre, étant inclinées, ces ondes ne se propagent pas vraiment le long de l'axe transversal, de sorte que la longueur d'onde telle que mesurée sur cet axe semble plus grande. Il suffit pourtant d'appliquer les transformations alpha à un système stationnaire transversal pour obtenir le système mobile équivalent. D'une part, il faut se référer à la longueur d'onde d'un système au repos. Et d'autre part, il faut réintroduire les équations de Lorentz pour les axes orthogonaux: y' = y; z' = y. Il est remarquable que la fréquence de ce système s'en trouve théoriquement ralentie, puisque la longueur d'onde telle que mesurée sur un axe transversal ne varie pas. Ce comportement préfigure donc ce qu'on verra plus loin dans le cas de l'électron. Mais ce n'est pas obligatoire, car on pourrait tout aussi bien se référer plutôt à une longueur d'onde contractée transversalement selon le facteur g, ce qui est le cas du son en présence de l'effet Doppler. Là encore, à cause d'un "effet de ciseau", on voit apparaître une onde de phase dont la vitesse sur l'axe du déplacement est égale à 1 / alpha. Étonnamment, il est difficile à priori de déterminer la vitesse alpha de ce système. En effet, on ne voit plus que cette onde de phase, qui présente une structure complexe rappelant celle d'un damier plus ou moins écrasé, tout dépendant de l'angle thêta.
Les "ondes stationnaires transversales animées". Les deux trains d'onde qui composent ce système ont la même longueur d'onde. Ces ondes circulent apparemment en sens opposé. Mais en réalité, elles se propagent selon un angle thêta valant : arc sin(alpha). Les franges d'interférence se déplacent vers l'avant à la vitesse de l'onde de phase, soit 1 / alpha. Ce phénomène est bien visible dans cette vidéo :
L'électron et la matière présentent déjà ces caractéristiques. Si l'on reproduit simultanément des ondes stationnaires orientées sur l'axe du déplacement et d'autres orientées sur un axe transversal, on obtient déjà une très bonne indication de l'aspect qu'aura l'électron en mouvement. Le comportement des ondes d'Ivanov constitue donc une indication de plus que l'électron est bel et bien fait d'ondes stationnaires sphériques, comme M. Milo Wolff l'affirmait depuis 1980. J'avais moi-même affirmé et publié dès 2002 que pour se mettre en mouvement, un tel système ondulatoire devait subir l'effet Doppler. Il subit plus exactement les transformations bêta proposées plus bas.
Voici le centre de l'électron en mouvement. L'onde de phase et la contraction du noyau central sont bien visibles. Bêta : 0,866; g = 0,5 (contraction : 50%).
On verra plus loin que dans le cas de la matière, tout est beaucoup plus simple. La distance absolue d'un point quelconque dont les coordonnées x, y et z d'un système de coordonnées cartésien présumé au repos dans l'éther sont converties selon le théorème de Pythagore est exprimée en secondes-lumière. La variable t représente le temps écoulé, évalué en secondes absolues. Poincaré disait plus justement: "l'instant t". Il est le même partout et il s'agit donc du "vrai temps" dans le sens où l'entendait Lorentz. Il ne s'agit plus d'une pulsation dont la période fluctue capricieusement selon la distance. Mais étonnamment, les équations requises demeurent pourtant strictement les mêmes. Elles indiquent que la contraction affecte réellement la matière et que les effets temporels affectent réellement l'heure affichée par les horloges. Ces effets se produisent pour des raisons mécaniques et ils sont mesurables d'une manière absolue par un observateur immobile comparativement à l'éther. Le problème. c'est que tout observateur en mouvement les perçoit plutôt d'une manière relative et tout à fait surprenante, et c'est là que la Relativité selon Lorentz prend tout son sens. C'est pourquoi Poincaré et Einstein, qui basent leurs prédictions sur ce que cet observateur en mouvement perçoit, semblent avoir raison. Le problème, c'est qu'ils ont tort sur les causes mécaniques réelles et fondamentales qui expliquent ces phénomènes. M. Ivanov a découvert pourquoi la matière se contracte. Dès maintenant, nous sommes en mesure de confirmer l'argument fondamental invoqué par M. Yuri Ivanov. À la seule condition que les liaisons chimiques impliquant les électrons de valence, les atomes et les molécules s'établissent en fonction d'une certaine longueur d'onde, ce qui est d'ailleurs bien admis de nos jours, toute matière en mouvement doit subir une contraction sur l'axe de son déplacement.
2 – LES TRANSFORMATIONS BÊTA (s'appliquent à l'électron). Voici les équations des transformations bêta de l'électron. On peut considérer qu'il s'agit tout simplement des transformations de Lorentz et de Poincaré, qui on le sait appliquaient ces transformations à l'électron et à ses champs électromagnétiques.
Les transformations bêta.
Il faut souligner d'abord et avant tout que les transformations "bêta" produisent un effet Doppler relativiste. C'est pourquoi la longueur d'onde de l'électron au repos vaut malgré tout la moyenne géométrique des deux longueurs d'onde qu'il produit vers l'avant et vers l'arrière lorsqu'il est en mouvement. C'est ce qui explique que les formules requises demeurent finalement identiques à celles qui s'appliquent aux ondes d'Ivanov. Ici, ce sont en fait les variables qui prennent une toute autre signification. Comme on l'a vu plus haut, avant d'appliquer les transformations, il est nécessaire d'effectuer un pré-calcul en fonction du système considéré. Ce qui distingue l'électron des ondes d'Ivanov, c'est que la longueur d'onde de l'électron au repos et sa fréquence sont réelles et constantes. Il n'est donc plus nécessaire de recourir à une moyenne géométrique, quoique ce calcul se vérifie de toutes façons puisque la fréquence de l'électron en mouvement ralentit. Avec x = 0 comme référence absolue, cette fréquence plus lente s'établit très simplement en fonction du facteur de contraction de Lorentz, comme la deuxième équation ci-dessus l'indique. t ' = g * t f ' = g * f J'ai déjà affirmé qu'il s'agissait de "l'équation du siècle" et je le pense toujours étant donné son importance. L'effet Doppler que subit l'électron est donc très particulier. On peut dire que c'est la découverte la plus significative de Lorentz. C'est ce qui lui a permis d'éliminer la constante "l" de ses équations. Poincaré a fait de même en suivant un autre chemin, ce qui l'a finalement conduit à son Postulat de Relativité. Les variables x, y et z représentent les coordonnées de l'électron au repos. On l'aura vu, l'électron est fait d'ondes stationnaires sphériques dont l'amplitude s'établit selon le sinus cardinal, soit: amplitude = sin(x) / x comme M. Jocelyn Marcotte l'a si bien démontré grâce à sa propre version (à trois dimensions!) du médium virtuel Delmotte-Marcotte. Mais attention : il ne faut pas confondre cette variable x avec la coordonnée x. La variable x du sinus cardinal avant sa conversion en radians représente la distance absolue d'un point situé en (x, y) comparativement à l'origine, où se situe le centre de l'électron au repos. Il faut donc recourir au théorème de Pythagore pour calculer la distance citée ci-dessous, et ensuite convertir cette distance en radians comme on l'a vu plus haut. Pour fixer les idées, les coordonnées x et y étant normalement exprimées en pixels sur l'écran d'un ordinateur, a dans ce cas particulier: distance en pixels = racine(x2 + y2) xradian = 2 * pi * distance en pixels / lambda en pixels amplitude = sin(xradian) / xradian Ici, les coordonnées x, y et z exprimées en pixels font référence à la longueur d'onde de l'électron au repos. Celle-ci est constante. Un jour, on arrivera certainement à la mesurer en suivant la piste de Louis de Broglie, mais il est clair qu'elle doit être inférieure à la taille d'un proton. La variable t représente la période de l'électron parfaitement stationnaire au point (x, y, z), à convertir là aussi en radians si l'on souhaite montrer cet électron sur l'écran de l'ordinateur. On peut le représenter en deux dimension, donc en tenant compte seulement des coordonnées x et y, car c'est bien suffisant pour s'en faire une idée correcte. Si par exemple la distance de l'origine exprimée en longueurs d'onde vaut 7, on aura aussi t = 7, à convertir au besoin en radians selon: 7 * 2 * pi. Il faut donc être conscient que, contrairement à ce que les équations de Lorentz semblent indiquer, il existe autant de "temps" t qu'il y a de pixels à évaluer, avant même d'effectuer la transformation bêta de l'électron. Les équations montreront alors un électron en mouvement pourvu qu'on convertisse les variables t' en radians et qu'on applique là encore le sinus cardinal. La vitesse à utiliser est bien la vitesse normalisée bêta donnée par Poincaré, que de Broglie appelle la "vitesse de groupe". Si vous suivez ces directives, vous devriez obtenir mon électron mobile. Il est très significatif que la formule mathématique qui permet de le représenter d'une autre manière, qui fut créée par M. Jocelyn Marcotte et simplifiée par M. Philippe Delmotte, produise exactement les mêmes résultats. Ce sont en effet les deux mêmes chercheurs géniaux qui ont créé le médium virtuel Delmotte-Marcotte. Ils ont toute mon admiration! D'ailleurs, cette preuve est d'autant plus solide qu'on peut aussi reproduire mon électron mobile d'une troisième manière, grâce à mon Scanner du Temps. Tout ceci s'avère remarquablement cohérent. amplitude = (sin(t + x) – sin(t) ) / x
L'électron au repos, à gauche, et sa version mobile, à droite. J'ai dû synchroniser la fréquence des deux systèmes à cause des contraintes inhérentes aux animations GIF. En réalité, la fréquence du système mobile montré à droite est plus lente selon : f ' = g f. Vous pouvez aussi observer l'électron mobile dans cette vidéo : Doppler_Moving_Electron.mkv Voici le programme qui m'a permis de la réaliser, et qui démontre que les transformations bêta fonctionnent admirablement : Doppler_Moving_Electron.bas Doppler_Moving_Electron.exe
Voilà donc pourquoi l'effet Doppler de l'électron diffère de l'effet Doppler acoustique normal. Cela explique la Relativité, qui est certainement vraie puisqu'elle a été vérifiée de différentes manières. C'est Henri Poincaré qui l'a décrite dès 1900 et qui en a formulé le principe dès 1904 sous le nom de "Postulat de Relativité". Mais ce n'est certainement pas pour les raisons mathématiques qu'il a proposées. Si la Relativité est vraie, c'est bien plutôt pour les raisons mécaniques invoquées par Lorentz, lesquelles s'appuient sur l'existence de l'éther. Cela dit, c'est au contraire à cause de la distorsion affectant les mesures effectuées par un observateur en mouvement que la Relativité se vérifie. Tout est là : la Relativité est le résultat d'une mystification. Elle est fondée sur les apparences. Pour la démontrer, on peut se baser sur certains effets. Par exemple, il n'existe qu'un seul taux de contraction qui soit compatible avec le décalage horaire qui s'ensuit, et qu'on peut facilement évaluer. C'est probablement la piste que Lorentz a suivie. On peut aussi démontrer qu'au moment où deux systèmes se rencontrent, toute contraction sur les axes orthogonaux (qui se produit effectivement dans le cas de l'effet Doppler normal) serait facile à détecter et indiquerait lequel des deux est le plus rapide comparativement à l'éther. Mais, depuis la découverte de la vitesse alpha, nous pouvons désormais énoncer un autre principe général qui y conduit :
Un exemple. Reprenons l'exemple d'un vitesse alpha de 0,5 tel qu'on l'avait proposé plus haut (les ondes d'Ivanov). On était en présence de deux ondes circulant théoriquement en sens opposé, l'une mesurant 50 pixels et l'autre, 150. Mais dans le cas présent, on a plutôt un électron au repos dont la longueur d'onde (lambda) telle que représentée sur l'écran est de 50 pixels. Or pour qu'un deuxième électron arrive à produire une longueur d'onde de 150 pixels vers l'arrière (lambda'), il doit s'éloigner de lui très rapidement. On a vu qu'il doit s'agir d'un effet Doppler relativiste (il pourrait tout aussi bien s'agir du "redshift" d'une galaxie éloignée), d'où le calcul suivant: bêta = 2 / ((lambda / lambda')^2 + 1) – 1 bêta = 2 / ((50 / 150)^2 + 1) – 1 = 0,8 c Le facteur de contraction de Lorentz : g = racine(1 – bêta^2) = 0,6 Le redshift relativiste : lambda' = lambda * (1 + bêta) / g La preuve : lambda' = 50 * (1 + 0,8) / 0,6 = 150
La vitesse requise étant 0,8 c, la vitesse intermédiaire moyenne arithmétique entre les deux électrons devrait être de 0,4 c. Pourtant, si un observateur se déplace entre ces deux électrons sur le même axe et à une vitesse alpha intermédiaire égale à 0,5 c (et non pas 0,4 c), il aura l'impression que les deux électrons s'éloignent de lui à la même vitesse, soit 0,5 c. Ce calcul s'appuie sur la loi de l'addition des vitesses relativistes élaborée par Henri Poincaré. bêta'' = (bêta + bêta') / (1 + bêta * bêta') Si l'on ajoute 0,5 à 0,5: bêta'' = (0,5 + 0,5) / (1 + 0,5 * 0,5) = 0,8 Si l'on ajoutait encore une fois 0,5 à 0,8, on obtiendrait: 0,92857. Étonnamment, cette vitesse est encore une fois inférieure à celle de la lumière. Le même calcul répété encore et encore produirait indéfiniment des vitesses inférieures à celle de la lumière (c = 1). C'est pour cette raison que Poincare affirmait dès 1904, à Saint-Louis, USA, que la vitesse de la lumière était une "limite infranchissable". Inversement, la vitesse moyenne alpha intermédiaire peut s'établir ainsi (bêta = 0,8; g = 0,6) :
Ou plus simplement : alpha = (1 – g) / bêta alpha = (1 – 0,6) / 0,8 = 0,5
Revoyons donc ce "Postulat de Relativité" et considérons encore ces deux électrons, l'un étant au repos et l'autre s'éloignant à la vitesse de 0,8 c. Entre les deux, un observateur se déplace sur le même axe à la vitesse intermédiaire alpha, soit 0,5 c. Les deux électrons émettent des ondes progressives l'un vers l'autre, dont la longueur est de 50 et 150 pixels sur l'écran de l'ordinateur. On a vu plus haut que ces ondes qui circulent en sens opposé doivent produire des ondes d'Ivanov. On peut obtenir leur vitesse de déplacement "alpha" grâce aux formules suivantes: R = lambda' / lambda = 150 / 50 = 3 alpha = (R – 1) / (R + 1) = 0,5 L'observateur se déplace donc exactement à la même vitesse que les ventres et les nœuds des ondes d'Ivanov. Cela signifie qu'il est incapable d'enregistrer les "battements" classiques, qui sont très perceptibles normalement si la longueur d'onde ou la fréquence diffèrent. Bref, à ses yeux, les deux fréquences semblent identiques. Puisque rien ne lui indique qu'il est en mouvement, cet observateur est tenté d'en conclure que ces deux électrons s'éloignent de lui sens opposé. Mais ce n'est pas tout : à cause de sa propre contraction (x' = 0,866 x) et du ralentissement de ses horloges (t' = 0,866 t), il fera erreur dans la mesure de ces longueurs d'onde et il trouvera que ces deux électrons s'éloignent de lui à la même vitesse alpha, c'est à dire la moitié de la vitesse de la lumière. C'est donc à cause d'une erreur dans ses lectures que l'observateur est totalement mystifié. Mais s'il est intelligent et bien informé, il doit être conscient qu'il pourrait tout aussi bien se déplacer à 0,5 c. Il pourrait même se déplacer à 0,8 c puisque dans ce cas l'un des électrons devrait se déplacer à 0,5 c et l'autre, à 0,92857 c comme on vient de le voir. Dans tous les cas, ses mesures seraient exactement les mêmes. En fait, il existe tout un éventail de solutions qui conviennent à ces mesures, et il lui est donc impossible de déterminer laquelle correspond aux faits absolus. Impossible de savoir ce qu'il en est exactement. Si donc nous observons deux galaxies s'éloigner de nous en sens opposé à la moitié de la vitesse de la lumière, nous devons faire face au même problème. En réalité, nous pourrions tout aussi bien nous déplacer nous-mêmes à la moitié de la vitesse de la lumière, et alors les résultats de nos mesures seraient parfaitement identiques. Dans ce cas, l'une des galaxies serait au repos et l'autre s'éloignerait à 0,8 fois la vitesse de la lumière. En fait, pour n'importe quelle vitesse de ces galaxies, il existe une vitesse intermédiaire alpha qui conduit à la même mystification tout à fait ahurissante, pour ne pas dire sublime... Voilà donc pourquoi la découverte de la vitesse alpha constitue un pas de géant. Elle permet de mieux comprendre la Relativité selon Lorentz, qui peut concilier la situation de trois référentiels distincts, alors que celle de Poincaré (ou d'Einstein) est limitée à deux à cause de sa belle mais trompeuse réciprocité. Je présente ci-dessous une autre illustration de ce phénomène, qui fait intervenir le test de Hertz. On constate que l'observateur obtient bel et bien deux longueurs d'onde identiques à l'aide de ce test, l'une à l'avant de lui et l'autre, à l'arrière. Veuillez noter que dans cet exemple, la vitesse bêta est de 0,5 alors que la vitesse intermédiaire alpha vaut 0, 2679 c. Ces faits sont facilement vérifiables. Prenez-en bonne note : à cause de la précision remarquable de nos instruments de mesure actuels, ce phénomène est devenu plus facilement vérifiable. Il n'est plus nécessaire de considérer des vitesses "relativistes". Dès qu'il aura été vérifié, les astronomes devront rejeter la théorie actuelle sur l'expansion de l'univers pour la remplacer par celle du Big Bang Relativiste. Jusqu'à maintenant, pour des raisons évidentes de simplicité, ils ont préféré considérer que l'univers prend de l'expansion un peu à la manière d'un pudding aux raisins qui gonfle au four. Puisque les raisins voisins s'éloignent à des vitesses de plus en plus rapides en fonction de la distance, du point de vue d'un raisin donné, il est impossible de déterminer où se situe le centre du pudding tant que les limites extérieures ne sont pas visibles. Non seulement elle est fausse, mais la "théorie du pudding" conduit à des erreurs additionnelles déplorables. Par exemple, M. Saul Perlmutter a dû déduire de ses observations que l'expansion de l'univers se faisait à une cadence accélérée. Cette erreur a ensuite conduit à toutes sortes d'interprétations farfelues, entre autres l'existence possible "d'énergie noire" qui serait responsable de cette accélération. En réalité, l'expansion de l'univers est relativiste. Si la vitesse des galaxies approche celle de la lumière, ces galaxies et l'espace qui les sépare se contractent. Là où leur vitesse frôle celle de la lumière se situe une sorte de "mur du temps" infranchissable. On peut même affirmer qu'à cause de la contraction, cette région contient à elle seule la quasi-totalité des galaxies de l'univers. Les astronomes devront réaliser que la lumière provenant des galaxies dont la vitesse excède 0,6 c montre un redshift relativiste indiscutable (en violet dans le graphique ci-dessous) puisque l'effet Doppler arrière dépasse alors le maximum possible de 2 fois la longueur d'onde normale (selon la courbe bleue, soit selon: 1 + bêta, sachant que bêta n'atteint jamais 1). Ces effets sont incompatibles avec la constante de Hubble à moins de considérer que ces galaxies se déplacent à des vitesses supérieures à celle de la lumière, ce qui serait en contradiction formelle avec la Relativité. Tout ça ne ressemble en rien à un pudding au raisin. En conséquence, il faudra corriger la constante de Hubble pour tenir compte des effets relativistes. Si on ne le fait pas, la luminosité des supernovae très éloignées de type 1A, qui on le sait est constante, semble faiblir davantage que selon le carré de la distance. C'est bien ce que M. Perlmutter a trouvé, mais il a dû parler d'une expansion accélérée de l'univers pour l'expliquer. Il faut souligner que ses recherches furent admirables et qu'il a obtenu des résultats vraiment significatifs. Un jour prochain, on fera la correction. Ce jour-là, M. Perlmutter deviendra célèbre parce qu'il aura démontré que la Relativité s'applique aussi à l'Univers...
Pour éviter tout malentendu, il devient nécessaire ici d'établir la différence entre l'effet Doppler normal, celui du son par exemple, et l'effet Doppler relativiste, soit celui qui caractérise l'électron, la lumière et les ondes radio:
On compare ici l'effet Doppler relativiste avec l'effet Doppler normal. L'effet Doppler relativiste est dû au ralentissement de la fréquence de l'électron selon sa vitesse : f ' = g f. Les effets sont ainsi bien différents selon qu'il s'agit d'un son ou de la lumière. Par exemple, le "redshift" d'une galaxie très éloignée (donc très rapide) vaut, en longueurs d'onde : (1 + bêta) / g. Dans le cas du son, on aurait plus simplement : 1 + bêta.
3 – LES TRANSFORMATIONS GAMMA (s'appliquent à la matière). Dans son esprit, les transformations établies par Lorentz s'appliquaient au départ à l'interféromètre de Michelson. Elles s'appliquaient donc à la matière, même si par la suite lui et Poincaré se sont tournés vers les champs électromagnétiques de l'électron. Mais là encore, même en parlant de l'électron et en appliquant ses transformations aux équations de Maxwell, le but premier de Lorentz était de montrer comment l'interféromètre se contracte de manière à annuler la différence de phase que Michelson prévoyait détecter. Il est très clair que Lorentz, de son propre aveu, "n'avait pas songé à la voie directe qui conduit à la Relativité", alors que Poincaré ne cherchait que ça. Dès 1901, dans Électricité et optique, Poincaré parlait déjà d'un "principe" voulant que les phénomènes optiques soient relatifs (ce qui est tout à fait faux et annonce son futur dérapage). En 1904, donc un an avant Einstein, il proclamait haut et fort à St-Louis (USA) son "Postulat de Relativité". Il en a fait une description suffisamment claire pour qu'on puisse affirmer qu'Einstein lui a purement et simplement dérobé sa découverte... Bref, Lorentz et Poincaré n'ont n'a pas fait la distinction entre la matière et les champs électromagnétiques. On verra ici que les transformations requises dans le cas de la matière, qu'on appellera "gamma", font appel une troisième fois aux mêmes équations. Mais au lieu de traiter des ondes, on fera appel à des unités d'espace et de temps. Pour ce faire, il convient de rappeler qu'on se réfère de nos jours à une fréquence donnée pour établir la longueur du mètre. Ici, pour respecter la normalisation proposée par Poincaré, on considérera une fréquence de 1 Hz. La longueur d'onde qui en résulte mesure une seconde-lumière, d'où : c = 1 seconde-lumière par seconde. Les variables x, y et z seront donc exprimées en secondes-lumière (300000 km) absolues, c'est à dire telles qu'on les mesurerait dans un repère cartésien réputé au repos comparativement à l'éther. Les variables t seront exprimées en secondes absolues et de la même manière. La vitesse normalisée bêta demeure la même que celle qui s'applique à l'électron, mais on parle plutôt ici de la vitesse d'entraînement d'un système matériel bien structuré, dans son ensemble, ce qui inclut ses espaces vides. On aura donc recours une troisième fois aux mêmes équations :
Les transformations « gamma » de la matière. Les grandeurs obtenues correspondent bel et bien à ce que Lorentz, Poincaré et Einstein ont tous proposé. En effet, même Albert Einstein prévoyait qu'un objet très rapide devrait nous apparaître plus court, soit selon g * x. Il devrait aussi sembler se déplacer conformément à : + bêta * t. Et enfin, tous s'entendent pour affirmer que le « temps ralentit » selon : g * t. On peut donc s'étonner que personne n'avait encore proposé ces formules...
Répétons-le, les variables x, y et z représentent ici les coordonnées d'un objet matériel immobile exprimées en secondes-lumière. Mais il faut surtout réaliser qu'ici, il n'existe qu'un seul temps t exprimé en secondes absolues, soit celui qui a cours partout dans un référentiel réputé au repos absolu comparativement à l'éther. Il s'agit du "vrai temps", selon le mot de Lorentz. Par contre, on obtient tout un éventail de temps t', qui représentent l'heure réelle mais inexacte affichée par les horloges en mouvement. La Relativité selon Lorentz nous autorise à établir par convention des normes d'espace et de temps, ici-même sur Terre, même si notre système solaire n'est sûrement pas au repos comparativement à l'éther. Quoi qu'on en pense, ces grandeurs arbitraires deviennent alors absolues, et tous n'ont qu'à s'y conformer... Contrairement à celles de Lorentz et de Poincaré, ces équations présentent l'immense avantage de comporter des variables x et x' dont les valeurs sont absolues et qui peuvent être reportées dans un unique référentiel cartésien présumé au repos dans l'éther. Ce ne sont pas l'espace et le temps qui se transforment, ce sont plutôt les dimensions d'un système matériel complexe et la vitesse d'évolution de ses processus mécaniques. Les effets des transformations gamma. Ces nouvelles équations sont bien plus transparentes quant à leurs effets, d'autant plus qu'elles indiquent bel et bien ce que Lorentz avait à l'esprit lorsqu'il a présenté sa théorie dans son mémoire de 1904. Voyez plutôt:
1 – La matière se contracte selon : g * x. Supposons qu'on a : bêta = 0,5 et g = 0,866. Dans ce cas, la partie d'un objet au repos située à: x = 1 seconde-lumière de l'origine se situe plutôt à x' = 0,866 seconde-lumière à l'instant t = 0 seconde si l'objet se déplace à cette vitesse. Pour des raisons mécaniques, cette contraction s'applique également aux espaces vides d'un système matériel complexe. En particulier, c'est à cause d'elle que l'interféromètre de Michelson devient incapable de mesurer la vitesse de la Terre à travers l'éther. 2 – Après un délai d'une seconde, ce même point aura avancé de : + bêta * t = 0,5 seconde lumière pour se situer finalement à 0,866 + 0,5 = 1,366 seconde lumière de l'origine. Il s'agit tout simplement d'un mouvement de translation, mais il faut d'abord tenir compte de la contraction.
3
–
Une horloge qui se déplace à la moitié de la vitesse de la lumière affiche des
secondes plus lentes selon : t' = g
* t comparativement aux secondes affichées par une horloge au repos. Pour
éliminer tout risque d'erreur dû à l'effet Doppler, il faut bien sûr que
la procédure de synchronisation des horloges soit effectuée à l'instant
précis où la distance qui les sépare est nulle. Pour faire simple, ce
devrait être au point x = x' = 0 et à l'instant t = t' = 0. Par la suite, à
l'instant t = 1 seconde, l'horloge en mouvement affiche donc 0,866 seconde et
elle a parcouru
0,5 seconde-lumière. 4
–
Les horloges présentent un décalage horaire qui correspond à : –
bêta * x. On se réfère ici à la position x d'une horloge
immobile, qui se situe donc en permanence à cette distance de l'origine peu importe le temps
écoulé. Si par exemple on a x = 1 seconde-lumière, l'horloge en mouvement
équivalente se situera au point x' = g * x
= 0,866 seconde-lumière à l'instant t = 0 seconde. Cette horloge accuse donc un retard de –bêta
* x = Les transformations réversibles de Poincaré. Les transformations bêta
produisent un effet Doppler si elles sont appliquées à un émetteur d'ondes
au repos. Mais elle peuvent tout aussi bien neutraliser cet effet Doppler s'il
est déjà présent puisque c'était effectivement le but de Voigt en 1887. Or
mon Scanner du temps peut réaliser les mêmes effets comme on peut le
vérifier ci-après. Toute l'astuce consiste à recourir à la vitesse
intermédiaire alpha, de manière à ce que le système de gauche se déplace
vers la droite tandis que celui de droite se déplace vers la gauche: Vous pouvez aussi télécharger une vidéo qui montre ce
phénomène : Time_Scanner_Doppler.mkv J'insiste donc sur le fait que
les transformations de Lorentz ont la propriété de produire un effet Doppler, mais qu'elles
peuvent tout aussi bien l'annuler si elles sont inversées. Seul, Poincaré a proposé deux séries d'équations dans ce
but, l'une étant le miroir de
l'autre, contrairement à Lorentz qui selon ses propres mots "n'avait pas
songé à la voie directe qui y conduit". Mon Scanner du Temps fait de
même, aussi bien avec les ondes d'Ivanov, les ondes de l'électron et la
matière en mouvement. Dans ce dernier cas, il annule la contraction et le
décalage horaire.
Henri Poincaré a donc proposé deux groupes d'équations dont l'un est le miroir de l'autre. Il parlait d'effectuer une rotation de 180° avant d'appliquer le deuxième groupe, mais cela équivaut plus simplement à revenir en arrière pour défaire les effets du premier groupe. Poincaré était persuadé qu'aucun de ces deux groupes n'avait préséance sur l'autre, ce qui était bien évidemment de nature à étayer son "postulat de Relativité". Poincaré l'ignorait, mais il est maintenant bien évident que la partie symétrique figurant à droite ci-dessous a plus simplement pour effet d'annuler l'effet Doppler que celle de gauche a produit. Or, même après correction et inversion, les équations montrées ci-dessous ne laissent pas deviner cette nuance capitale à moins de préciser d'entrée de jeu que les variables x et t ont préséance sur les variables x' et t'. Ce qui est clair aujourd'hui, c'est qu'un système au repos a préséance sur un système en mouvement. Un système sans effet Doppler a donc préséance sur un autre qui en est affecté. Il s'agit du fameux "référentiel privilégié" qu'on invoque lorsqu'on parle de la Relativité selon Lorentz. La Relativité n'est donc pas réelle: elle ne peut être que le résultat d'une illusion attribuable à des mesures faussées à cause des transformations de Lorentz. Voici donc ces équations symétriques après inversion et correction :
Le groupe complet des transformations de Lorentz, revu et corrigé.
PLUSIEURS CHERCHEURS ONT PROPOSÉ DE TELLES TRANSFORMATIONS Revenons sur l'expérience de Michelson et Morley, qui ont réalisé à partir de 1887 des expériences de plus en plus précises à l'aide d'un interféromètre. On sait que cet appareil n'a pas fonctionné comme Michelson le prévoyait. En principe, ce fut un échec. Mais ce résultat inattendu devait forcément lever le voile sur une "mécanique nouvelle" propre à la matière (cette expression est de Poincaré). On peut dire que Michelson a fait, et c'était déjà très clair à l'époque, l'une des plus grandes découvertes scientifiques de tous les temps. C'est ce qui a incité beaucoup de chercheurs à participer à cette grande aventure. Woldemar Voigt. En 1887, donc avant le début des tests de Michelson, Woldemar Voigt avait proposé un groupe d'équations dont le but était de neutraliser l'effet Doppler dans un référentiel en mouvement. Il les appliquait aux équations de Maxwell. Il semble que Lorentz n'ait pas eu connaissance des travaux de Voigt lorsqu'il a mis au point ses premières équations vers 1895. Voici une transposition des équations de Voigt qui me semble suspecte :
Ces équations sont manifestement inexactes puisque le facteur "q", qui correspond au facteur de contraction de Lorentz "g", affecte les coordonnées y et z. Pourtant, Lorentz a reconnu après 1905 que les équations de Voigt équivalaient aux siennes, ce qui donne fortement à penser que celles-ci sont inexactes. Vers l'an 2000, j'avais d'ailleurs moi-même trouvé sur l'Internet une version très différente, qu'on attribuait pourtant à Voigt. En particulier, elle comportait une constante "k" qu'on retrouve également sous la forme "l" dans la version de Lorentz. Il faudra donc tirer ceci au clair. Par contre, je suis en mesure d'affirmer que cette autre version attribuée à Voigt est proprement géniale. Il y a un bémol : grâce à mon ordinateur, j'ai découvert que si l'on désire conserver cette constante, que j'appellerai la constante de Voigt "k", elle doit figurer au numérateur dans l'équation x' et au dénominateur dans l'équation t'. J'ai donc fait la correction dans la version montrée ci-dessous. Il s'agit là d'une erreur grave qu'on n'a jamais remarquée semble-t-il puisque cette constante fut éliminée. Et bien évidement, là encore, il a fallu inverser ces équations de manière à attribuer les variables x' au système en mouvement.
Les transformations de Voigt revues et corrigées. La constante k est utile car elle permet de produire ou de corriger un effet Doppler à fréquence variable. Dans le cas de l'effet Doppler normal, la constante k est égale au facteur g de manière à maintenir la même fréquence. Dans le cas de la lumière et des ondes qui composent la matière, la constante k est égale à 1 de manière à ralentir la fréquence.
Ce groupe d'équations produit un effet Doppler "variable". C'est dû au fait que la constante k permet de modifier la fréquence du système. Par exemple, Lorentz ayant trouvé que la valeur de cette constante devait être égale à 1 (ce qui permet de l'éliminer pour aboutir aux transformations de Lorentz classiques), on obtient un effet Doppler relativiste. Dans ce cas, la fréquence du système ralentit selon le facteur g. Mais si la constante k est égale au facteur g, on obtient plutôt l'effet Doppler acoustique normal, qui bien sûr n'implique aucune modification de la fréquence. Cela signifie par exemple que, dès qu'on est en présence d'un effet Doppler impliquant les ondes radio émises par un satellite, il s'agit en soi d'un "effet relativiste". Il faudra à l'avenir prendre garde à cette particularité, car les physiciens avaient l'habitude de ne tenir compte des effets relativistes qu'en présence de vitesses énormes. N'en doutez pas, même les calculs impliquant les satellites GPS doivent tenir compte des effets relativistes. En effet, un observateur posté dans un satellite n'enregistre aucun effet Doppler dans les ondes que ses antennes émettent parce que tout son environnement se transforme de manière à compenser. Or il y en a manifestement un, et il est considérable. J'ai écrit le programme ci-après dans le but de montrer les quatre transformations les plus significatives. Elles correspondent aux choix A, B, C or D. Avec k = 1, on obtient donc les transformations de Lorentz, qui se caractérisent par un ralentissement de la fréquence selon le facteur g, ce manière à obtenir une invariance dans la longueur d'onde sur les axes orthogonaux : x' = x; z' = z. Doppler_Voigt_transformations.bas Doppler _Voigt_transformations.exe Ce programme permet aussi d'obtenir l'effet Doppler normal, qui on le sait produit une contraction de la longueur d'onde sur les axes orthogonaux selon le facteur g. Il s'agit sans doute de la manière la plus facile d'obtenir un effet Doppler sur l'écran d'un ordinateur. Ces équations seront donc utiles dans le futur à beaucoup de gens. C'est pourquoi j'ai pris la peine de les simplifier, sachant qu'on a k = g.
L'effet Doppler normal. Soyez sans crainte, ces équations ne s'appliquent pas à priori aux équations de Maxwell ! Les variables x, y, et z représentent les coordonnées d'un pixel sur votre écran, exprimées en longueurs d'onde. La variable t indique la période en cours pour ce pixel, considérant sa distance de l'origine, en longueurs d'onde. Pour afficher l'onde sans effet Doppler, il faut donc la convertir en radians : sin(t * 2 * pi) sur le pixel x, y. Pour afficher l'onde avec effet Doppler, on aura plutôt : sin(t' * 2 * pi) sur le pixel x', y'.
Heaviside et FitzGerald. En 1889, Oliver Heaviside fit valoir que les charges électrostatiques devraient se contracter selon un facteur de contraction équivalent au futur facteur g de Lorentz, déjà connu sous le nom de "l'aberration". Son ami George FitzGerald proposa alors d'appliquer la même contraction à l'interféromètre de Michelson. FitzGerald avait parfaitement raison sur ce point. Par contre, il n'a jamais publié cette hypothèse ni présenté les équations correspondantes. Il n'a pas signalé d'effets temporels non plus. Lorentz cite toutefois FitzGerald dans son mémoire de 1904, de sorte que la contraction qu'il ont proposée mérite certainement d'être nommée "contraction Lorentz-FitzGerald". Joseph Larmor. En 1897, Joseph Larmor proposa des transformations indiquant seulement un mouvement de translation selon v * t. Sa première théorie était basée sur le fait que la contraction de l'interféromètre de Michelson devait être le résultat des effets temporels, ce qui est tout à fait génial. De plus, c'était un fervent partisan de la théorie de l'éther, qu'il a lui-même fait progresser énormément. De ce point de vue, ce grand personnage fut le seul à être totalement en accord avec la Relativité selon Lorentz. En 1900, dans son livre intitulé "Éther et Matière", on constate qu'il maîtrise déjà assez bien les transformations de Lorentz, mais la contraction n'est toujours pas donnée correctement (ci-dessous, on a x' = x – v * t). On y retrouve le facteur de contraction de Lorentz et son équation du temps indique le décalage horaire correct. Or même en 1904, le décalage horaire proposé par Lorentz était toujours inexact.
Par contre, on sait que Joseph Larmor suivait de près les progrès de Lorentz (et sans doute inversement), de sorte qu'il est difficile de déterminer quelle fut la contribution réelle de l'un et de l'autre. En 1901, Poincaré mentionne clairement que Larmor a adapté la théorie de Lorentz à la sienne. La même confusion existe d'ailleurs entre Lorentz et Poincaré, qui ont échangé de la correspondance. Il faudrait faire une étude là-dessus pour y voir plus clair. Quoi qu'il en soit, l'œuvre de Larmor est significative et ce fut certainement un très grand chercheur. Yuri Ivanov. En 1981, M. Yuri Ivanov proposa ses propres transformations:
Les transformations d'Ivanov (1981).
Ces équations ne sont pas sans intérêt. Elles sont le reflet du comportement des ondes qu'il a découvertes : les ondes d'Ivanov. Or on a vu que ces ondes pouvaient tout aussi bien être évaluées selon la moyenne arithmétique ou géométrique des deux longueurs d'onde en cause. Mais alors les formules requises diffèrent. M. Ivanov propose une contraction selon le facteur g sur les axes transversaux y et z. Il propose une contraction encore plus sévère sur l'axe du déplacement, soit selon le facteur g au carré. Cela correspond à l'effet Doppler acoustique, ce qui est normal puisqu'il a mené ses tests au moyen de microphones et de haut-parleurs en présence de vent. Son équation du temps fait aussi référence à l'effet Doppler acoustique, qu'on peut en effet évaluer selon un angle de propagation thêta puisqu'il est sinusoïdal. Ce tableau est doublement intéressant parce qu'il montre aussi les transformations de Galilée, qui conduisent à son célèbre "principe de Relativité". Ce mot de Relativité est donc implicite dès qu'on parle de transformations spatio-temporelles. Mais en fait, on parle ici beaucoup plus simplement d'un mouvement de translation, qui peut être envisagé différemment par deux observateurs postés dans des référentiels dont la vitesse n'est pas la même. x ' = x – v t t ' = t Si donc ou utilise la méthode de Poincaré (revoir le tableau déjà montré beaucoup plus haut), il suffit de permuter les variables et d'inverser le signe pour obtenir le point de vue de l'autre observateur dans une équation parfaitement symétrique. x = x ' + v t ' Henri Poincaré. En 1901, dans son livre "Électricité et optique", Henri Poincaré expose la théorie de Lorentz même si ce dernier ne l'a pas encore publiée. Il présente ses propres équations en précisant qu'elles sont de Lorentz et en les nommant même d'après lui. Ces équations indiquent un mouvement de translation alors que celles de Lorentz ne le feront pas. Elles présentent aussi la fameuse constante "l" (que j'appellerai la constante de Voigt) qui permet de varier la fréquence. Poincaré ajoute que Lorentz a déjà trouvé "par tâtonnements" que cette constante devrait être égale à 1. Il est lui-même d'accord avec ce choix parce qu'il respecte le "principe de moindre action" (c. f. Maupertuis, Euler, Lagrange). Il faut insister sur le fait que Poincaré fut particulièrement séduit par la théorie de Lorentz parce qu'il avait lui-même œuvré à la "Commission des Longitudes". Il s'était interrogé sur les résultats d'une procédure de synchronisation des horloges par signaux optiques. Le problème, c'est qu'il devait forcément se produire un décalage horaire à cause du mouvement de la terre comparativement à l'éther. Or les équations de Lorentz tenaient compte d'un tel décalage horaire. Je dois dire que la description que Poincaré en fait dans ses livres est inexacte parce qu'il a toujours refusé de prendre en compte la contraction de la matière. Par contre, les équations qu'il utilise en 1901 indiquent bel et bien le décalage horaire correct, qui correspond à: –bêta * x. Je rappelle que c'est Joseph Larmor qui semble avoir devancé Poincaré et même Lorentz sur ce point, soit en 1900. J'ai mis ci-dessous une copie des équations présentées en 1905 par Poincaré. Elles sont plus exactes et mieux formulées que celles de Lorentz (1904). En particulier, le mouvement de translation y figure et Poincaré a bien vu que la vitesse de la lumière pouvait être ramenée à la valeur nominale de 1 de manière à ce que son carré demeure aussi égal à l'unité. Poincaré a pu alors simplifier encore davantage les équations en normalisant aussi la vitesse, représentée alors par la lettre grecque epsilon mais aujourd'hui par bêta. Il s'y trouve aussi l'inverse du facteur g, représenté par la lettre "k", et devenu le célèbre facteur "gamma", qu'on retrouve aujourd'hui dans tous les ouvrages sur la Relativité. Après toutes ces années, au fur et à mesure que je compilais tous ces renseignements, j'ai été amené à faire des commentaires qui ne se sont pas toujours avéré pertinents. C'est donc avec la plus grande prudence que j'avance maintenant que les véritables "transformations de Lorenz", dans leur forme définitive, semblent bien être une autre des nombreuses réalisations de Poincaré. À cause de sa modestie bien connue, il aura tout simplement négligé de revendiquer la paternité de ces innovations. On peut citer aussi, entre autres: le Postulat de Relativité, la loi de l'addition des vitesses relativistes, l'équation E = mc^2 dans une forme inversée, la "mécanique nouvelle", la similitude entre l'inertie et la gravité, etc. Aujourd'hui, tout ceci est attribué à Einstein, de sorte que je peux affirmer sans la moindre retenue que tous ceux qui ne jurent que par Albert Einstein sont des ignorants. Après tout, on parle ici d'un très grand nombre de publications allant de 1895 à 1904, avec des tas d'autres références extérieures, alors qu'Einstein n'a publié "sa" version qu'en 1905. Il a prétendu que son travail avait été indépendant alors qu'on sait très bien qu'il résumait régulièrement pour les Annalen der Physik les travaux de physique les plus intéressants de l'époque. Il connaissait donc forcément toutes ces publications, en particulier la célèbre "Note à l'Académie" de Poincaré, reçue en 1905 avant qu'il ne publie lui-même son texte sur la Relativité. Or on ne peut retrouver la moindre preuve à l'effet qu'il a vraiment travaillé là-dessus. Très franchement, si l'on considère que trois physiciens éminents de la trempe de Lorentz, de Poincaré et de Larmor ont mis dix ans pour élaborer la Relativité, il est tout simplement impossible qu'Einstein y soit parvenu seul en aussi peu de temps. La vérité, c'est qu'Einstein a copié Poincaré avec une rare effronterie. Tous ceux qui se noieront un jour dans son sillage auront fait preuve d'une mauvaise foi inqualifiable. Je vais donc omettre de citer Einstein. C'est d'autant plus pertinent que les équations de ce dernier sont, là encore, identiques à celles de Poincaré (quoique déguisées, comme tout bon plagiaire sait le faire). Malheureusement pour Einstein, les idées de Poincaré sur la Relativité étaient erronées. Seule, la Relativité selon Lorentz peut s'expliquer logiquement sans avoir recours à des concepts ésotériques et farfelus. Voici donc les transformations dites "de Lorentz", mais selon toute vraisemblance attribuables à Henri Poincaré :
Une splendeur : les transformations de Poincaré (1905). Ici, epsilon représente la vitesse normalisée bêta et k, le facteur de contraction de Lorentz g. La constante de Voigt "l" peut être supprimée puisqu'elle est égale à 1.
Hendrik Antoon Lorentz.
À mon avis, la découverte fondamentale de Lorentz est ce qu'on a appelé à tort le "ralentissement du temps". Il s'agit plus exactement du ralentissement de la fréquence de l'électron en fonction du facteur g, ce qui provoque un ralentissement de tous les phénomènes mécaniques. Bref, ce n'est pas le temps qui ralentit, ce sont plutôt les horloges en mouvement qui égrènent des secondes plus lentes. J'oserai affirmer que l'équation du temps donnée par Lorentz est incorrecte puisque c'est le décalage horaire donné par Larmor en 1900 et confirmé par Poincaré en 1901 qui s'avère exact. Par contre, Lorentz donne le ralentissement des fréquences correct. C'est précisément en raison de ce ralentissement que l'effet Doppler est modifié de telle sorte que la longueur d'onde ne se contracte pas sur les axes y et z. En effet, l'effet Doppler normal a pour effet de contracter la longueur d'onde sur ces axes selon le facteur g. C'est donc Lorentz qui a trouvé le premier qu'on doit obtenir: x' = x; z' = z. La Relativité n'est possible qu'à cette condition. Les idées de Lorentz sont exposées dans son mémoire présenté à l'Académie d'Amsterdam en 1904. Comme vous pouvez le constater, ses équations diffèrent sensiblement de celles de Poincaré montrées ci-dessus.
Les équations de Lorentz, telles que présentées en 1904. Veuillez noter que k représente le facteur gamma et non le facteur de contraction g, qui vaut l'inverse. La constante de Voigt "l" y figure toujours, même si elle est devenue inutile ( l = 1).
On remarque en particulier l'absence de mouvement de translation, quoique certains prétendent que la variable x est déjà modifiée ici selon: x* = x – v t. C'est possible, mais je n'ai personnellement rien vu de tel dans le mémoire de 1904. D'ailleurs, le fait d'appliquer ces formules aux équations de Maxwell complique tellement la démonstration qu'on s'y perd. Mais ça n'a guère d'importance car ce sont surtout les effets temporels et la contraction qui sont déterminants. Sachant que les variables x', y' et z' s'appliquent ici au référentiel au repos, ce qui est extrêmement trompeur, on obtient une dilatation et non une contraction. De la même manière, le ralentissement de la fréquence se traduit ici par une accélération. Pour être franc, je préfère de loin la formulation de Poincaré montrée plus haut.
LA LOI DE L'ADDITION DES VITESSES DE POINCARÉ Selon Lorentz, l'inertie augmente avec la vitesse de telle sorte que la vitesse de la lumière devient une limite infranchissable. Dans ces conditions, le fait pour un observateur d'accélérer à la moitié de la vitesse de la lumière alors qu'il se déplace déjà à la moitié de la vitesse de la lumière du point de vue d'un deuxième observateur ne peut pas se traduire selon ce dernier par une simple addition des vitesses puisqu'on aboutit alors à la vitesse de la lumière. Ce pourrait même être pratiquement le double à la limite puisque la vitesse d'un objet peut approcher celle de la lumière. Il doit donc exister une loi de l'addition des vitesses qui respecte les transformations de Lorentz. Sachant cela, Henri Poincaré a élaboré la formule suivante : bêta'' = (bêta + bêta') / (1 + bêta * bêta') Dans l'exemple ci-dessus, deux fois la moitié de la vitesse de la lumière équivaut à 80% de la vitesse de la lumière. S'il faut additionner bêta = 0,1 à bêta' = 0,2 on obtient bêta'' = 0,294 et non pas bêta'' = 3. Mais soyons clairs. Cela signifierait par exemple que le pilote d'une fusée spatiale qui se déplace déjà selon nous sur Terre à bêta = 0,1 entreprend d'accélérer jusqu'à bêta' = 0,3. On sait que selon la Relativité il se considère au repos. S'il réussit son exploit, il considérera donc qu'il se déplace maintenant à bêta' = 0,3 alors que selon nous il aura accéléré sa vitesse de bêta' = 0,1 à bêta'' = 0,294. Mais pour être parfaitement logique, ce pilote devrait considérer que, puisqu'il est parti de la Terre et qu'il a déjà ressenti fortement les effets de l'accélération qui l'a d'abord propulsé à 10% de la vitesse de la lumière, il n'était plus en droit de se considérer toujours au repos. C'est donc le point de vue d'un observateur sur Terre, dont les mesures n'ont pas changé, qui prime sur le sien. On voit l'utilité d'établir par convention un référentiel privilégié. Encore une fois, la Relativité de Lorentz se révèle ici supérieure à celle d'Einstein ou de Poincaré, celle-ci étant incapable de concilier ces trois référentiels distincts à cause de son inévitable réciprocité.
LES TRANSFORMATIONS TOUS AZIMUTS Mais il y a plus encore : si l'on envisage de transformer un grand nombre de galaxies en les montrant sur un même tableau, il devient nécessaire de modifier les coordonnées x, y et z en conséquence. À petite échelle, on peut considérer comme l'a fait Lorentz qu'un objet circule constamment sur un axe x et qu'on a par ailleurs: y' = y et z' = z. Mais ce n'est plus possible si l'univers est en expansion. Il devenait donc nécessaire de mettre au point des équations tridimensionnelles, ce que j'ai fait...
Une nouveauté : les transformations tridimensionnelles tous azimuts. Elles s'appliquent en priorité à l'univers, qui est en expansion. Mais elles permettent aussi d'effectuer les transformations de Lorentz peu importe l'axe du déplacement. La formule : gxyz = gx * gy * gz introduit une nouveauté : la loi de l'addition des composantes de vitesse. Henri Poincaré avait énoncé une loi similaire sur l'addition des vitesses, la vitesse de la lumière devenant inaccessible.
J'ai poli et repoli ces équations en mai et juin 2009 pour leur donner une beauté formelle qu'elles n'avaient pas au départ. Reproduite à l'aide de ces équations, même l'onde de phase découverte par Louis de Broglie se révèle remarquablement précise. Cela garantit que l'émetteur d'onde, qui doit faire appel à cette onde de phase, produira dans le médium virtuel Delmotte-Marcotte un effet Doppler pour ainsi dire parfait peu importe l'axe de son déplacement.
Les transformations tous azimuts permettent de travailler dans un espace à deux et même à trois dimensions. On peut obtenir un effet Doppler relativiste, une contraction selon Lorentz et une onde phase quelle que soit la direction du système ! Big_Bang_03_Multiple_Doppler.mkv Le programme FreeBASIC : Big_Bang_03_Multiple_Doppler.bas
Ces équations sont d'une grande beauté. Les animations ci-dessous montrent très bien de quoi elles sont capables, et elles me plaisent infiniment. Il s'agit certainement de la réalisation mathématique la plus significative que j'aie menée à terme à ce jour... L'effet Doppler sur un trajet oblique, dans le médium virtuel Delmotte-Marcotte : Relativistic_Doppler.avi Mon électron mobile, également sur un trajet oblique : Doppler_Moving_Electron_Diagonal.avi L'onde de phase de Louis de Broglie, dans le contexte de l'expansion de l'univers : Big_Bang_04_Phase_Wave.mkv D'ailleurs, je n'ai pas hésité à transformer Lorentz lui-même : Lorentz_3D_Transformations.mkv C'est ce qu'on pourrait appeler la transformation de Lorentz ! La contraction en particulier est évidente. Le but véritable était de montrer que l'onde de phase doit être associée à la contraction (il faut la situer dans une ellipse et non un cercle) pour qu'elle se superpose parfaitement à l'effet Doppler relativiste. Voici une illustration encore plus révélatrice de ce phénomène: L'onde de phase de Louis de Broglie, sur un trajet oblique : Phase_Wave_2.mkv Vous trouverez plus de détails sur ces transformations à la page sur le Big Bang relativiste.
Le Scanner du Temps fait mieux encore. Voici une vidéo plus complète qui devrait vous intéresser au plus haut point. Je vous préviens, elle est quelque peu indigeste au premier abord car elle contient tous les éléments qui permettent de démontrer que la version de la Relativité proposée par Lorentz en 1904 était correcte : Et voici le programme FreeBasic qui a produit cette animation: Avouez que mon Scanner du Temps est l'outil idéal pour montrer comment l'observateur B voit les choses de son propre point de vue, c'est à dire en postulant qu'il est au repos. Il réalise donc ici la même chose que les équations proposées par Lorentz et Poincaré, à savoir remettre l'électron mobile dans un repère au repos. On voit aussi qu'il est possible de montrer un nombre illimité de référentiels dans la même scène, ce que la Relativité d'Einstein est incapable de faire à cause des mesures incompatibles. De plus, on constate que la règle graduée rouge ne subit aucune transformation de longueur. Cela démontre qu'il est ridicule d'invoquer une transformation de l'espace puisqu'elle ne s'applique pas nécessairement. Pour ceux qui n'auraient pas encore saisi comment le Scanner du Temps arrive à reproduire les transformations de Lorentz, je rappelle que le balayage qu'il réalise doit se faire à la même vitesse que celle de l'onde de phase, soit 1 / bêta. Je tiens aussi à rappeler que tout observateur en mouvement va à la rencontre de la lumière et des ondes radio si elles proviennent de l'avant. Inversement, il les fuit si elles proviennent de l'arrière. Ne cherchez pas plus loin, tout repose sur ce phénomène: un observateur mobile voit ce qui se passe devant lui avant ce qui se passe derrière lui. Il est victime d'une distorsion évidente qui lui permet de corriger l'effet Doppler dans les ondes que lui-même émet de manière à ce qu'elles lui semblent parfaitement sphériques; il voit au contraire un effet Doppler dans les ondes provenant d'un émetteur au repos. C'est exactement ce que les équations réversibles présentées par Henri Poincaré produisent. Mais les conclusions de Poincaré étaient fausses, car les phénomènes optiques ne sont pas relatifs comme il le pensait. La vérité, c'est que les événements tels qu'ils sont perçus par un observateur en mouvement présentent une distorsion spatio-temporelle. Cet observateur est manifestement victime d'une mystification. Le Scanner du Temps est remarquablement efficace. Le Scanner du Temps est en mesure d'effectuer les transformations de Lorentz sur tous les éléments d'une même scène, peu importe leur vitesse et leur direction propres. Bien évidemment, chacun de ces éléments doit avoir été transformé au préalable avant de subir une deuxième transformation. Ci-dessous, on a par exemple une roue dentée entraînée par des engrenages théoriquement circulaires. Son centre est au repos. Mais à cause de la vitesse de rotation, ces engrenages qui se déplacent à 0,866 fois la vitesse de la lumière sont contractés de moitié selon le facteur g. C'est pourquoi ils apparaissent elliptiques. Le balayage a pour effet de transformer l'ensemble de manière à montrer quelle serait sa structure s'il était accéléré à 0,866 fois la vitesse de la lumière. Ce n'est pas évident du tout à première vue, mais le résultat respecte admirablement la Relativité. Par exemple, on pourrait croire que la vitesse des dents supérieures de la roue, qui se déplaçaient déjà à 0,866 fois la vitesse de la lumière, devrait atteindre le double puisqu'on a accéléré toute la roue à cette même vitesse. Pourtant, un objet ne peut jamais atteindre la vitesse de la lumière. C'est une application de la loi de l'addition des vitesses relativistes de Poincaré: bêta prime = (bêta_1 + bêta_2) / (1 + bêta_1 * bêta_2) = (0,866 + 0,866)/(1 + 0,866 * 0,866) = 0,9897.De plus, sachant que le temps t' indique que tout ce qui est à l'avant est en retard sur ce qui est à l'arrière, les dents de la roue avancent plus lentement dans le haut de l'image de droite de manière à respecter ce retard...
L'optique du mouvement. Il faut souligner que tous les dérapages sur la Relativité n'auraient jamais eu lieu si les physiciens qui ont participé à son élaboration avaient possédé une meilleure connaissance de l'optique. Au lieu de recourir aux équations de Maxwell, ils auraient dû plus simplement étudier de quelle manière la lumière se comporte lorsqu'on fait intervenir le mouvement. Après tout, c'était bien ce que l'interféromètre de Michelson devait analyser. Puisqu'on ne l'a toujours pas fait, ce qui est vraiment consternant si l'on considère l'importance de ces phénomènes, j'ai dû jeter les bases de l'optique du mouvement. Je dirais même que l'ignorance actuelle des phénomènes optiques et acoustiques, en particulier lorsque le mouvement intervient, est scandaleuse. Bien qu'il ait été mis au point il y a des années, le monde scientifique n'a toujours pas réalisé que le médium virtuel mis au point par Philippe Delmotte et Jocelyn Marcotte constitue un outil indispensable lorsque vient le temps d'étudier le comportement des ondes. Un jour, n'en doutez pas, tous les étudiants en optique et en acoustique ne travailleront qu'avec ça. La Relativité. La Relativité selon Lorentz sera désormais plus facile à comprendre. L'interféromètre de Michelson se contracte vraiment comme Lorentz l'a indiqué. Mais hélas ! à cette époque, il en ignorait la raison. Son hypothèse a donc été rejetée comme improbable. Mais depuis ce temps, Louis de Broglie a montré que l'électron diffracte comme le font les ondes. Et plus récemment, M. Yuri Ivanov a montré que les ondes stationnaires se contractent si le mouvement intervient. Il a fait valoir que, puisque les liaisons atomiques et moléculaires s'effectuent en fonction de la longueur d'onde des électrons de valence, ce qui est bien admis de nos jours, la matière en mouvement doit se contracter. Soyons clairs, les faits sont absolus. Mais la Relativité est vraie car les faits sont perçus comme s'ils étaient relatifs. Soyons clairs, l'espace et le temps ne se transforment pas. C'est plutôt la matière en mouvement qui se contracte, et ce sont tous ses mécanismes qui fonctionnent plus lentement. Il n'y a plus de paradoxes. Tout devient clair et logique. |
| 01 | 02 | 03 | 04 | 05 | 06 | 07 | Vous êtes ici. | 09 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 |
|
Gabriel La Frenière, Bois-des-Filion en Québec. Sur l'Internet depuis septembre 2002. Dernière mise à jour le 15 février 2011. Courrier électronique : veuillez consulter cet avis. La théorie de l'Absolu, © Luc Lafrenière, mai 2000. La matière est faite d'ondes, © Gabriel Lafrenière, juin 2002. |