LE BIG BANG RELATIVISTE
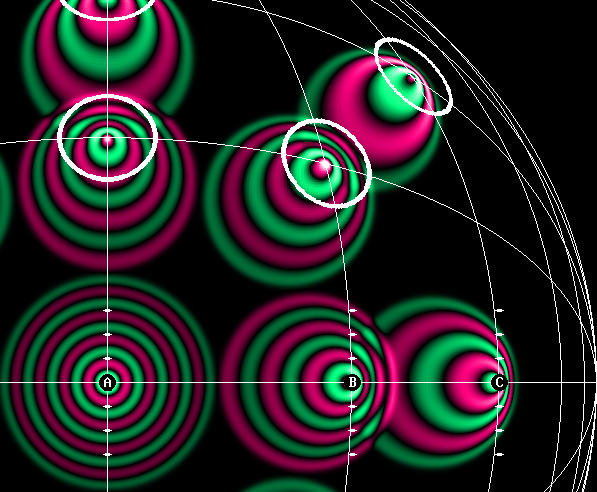
Le "redshift" dans la lumière des galaxies éloignées est forcément relativiste.
Plus la galaxie est éloignée et donc rapide selon la constante de Hubble, plus la fréquence de la lumière qu'elle émet ralentit.
Remarquer l'invariance transversale de la longueur d'onde, qui est la caractéristique majeure de l'effet Doppler selon les transformations de Lorentz.
De cette manière, l'observateur B montré ci-dessus peut considérer qu'il est au repos, et même qu'il se situe au centre de l'univers.
![]()
![]() Page
d'accueil : La matière
est faite d'ondes.
Page
d'accueil : La matière
est faite d'ondes.
LA RELATIVITÉ TRIDIMENSIONNELLE
La sphère cosmique.
|
La Relativité s'applique à tout en ce monde. Mais à cause de leur vitesse considérable, elle s'applique d'abord et avant tout aux galaxies les plus éloignées. Très clairement, ces galaxies sont donc assujetties aux transformations de Lorentz. Cela signifie que nous devrions observer une contraction de leurs dimensions dans le sens de leur déplacement, un ralentissement de la fréquence de la lumière qu'elles émettent et un "temps local" variant selon leur distance. Nous savons que les galaxies qui nous entourent semblent s'éloigner selon la constante de Hubble. Plus elles sont éloignées, plus elles sont rapides. Notre univers étant manifestement en expansion, il est raisonnable de penser qu'il a pu se produire un "Big Bang" à l'origine, ou à tout le moins une naissance de notre univers dans un espace relativement restreint suivie d'une expansion dans des proportions fantastiques. Or une telle expansion ne peut se faire que conformément aux transformations de Lorentz et donc à la Relativité. Il en ressort que la distance réelle des galaxies les plus rapides, celles dont la vitesse approche celle de la lumière, a été mal évaluée jusqu'à maintenant. Si la Relativité est vraie, et elle l'est, les galaxies doivent forcément sembler se situer en plus grand nombre relativement près de la surface d'une énorme sphère, déjà connue sous le nom quelque peu ésotérique de "sphère cosmique". C'est pourquoi, selon toute vraisemblance, nous devons nous représenter les galaxies de l'univers selon le modèle représenté ci-dessous.
La sphère cosmique. Pour fixer les idées, on a ici une vitesse de référence bêta = 0,5 arbitraire qui détermine une vitesse intermédiaire alpha = 0,2679. Vues du centre A, les galaxies nous apparaissent d'autant plus rapides et contractées qu'elles se situent près de la surface de la sphère. Mais étonnamment, un observateur situé dans une autre galaxie, B par exemple, a quand même l'impression qu'il se situe au centre. C'est dû au fait qu'il va à la rencontre des ondes de la lumière, qui l'informent de la situation. Il en résulte une distorsion dans le temps entre ce qu'il voit à l'avant et à l'arrière. Le Scanner du Temps peut reproduire cette distorsion en balayant l'arrière de la scène à une époque bien plus ancienne qu'à l'avant. Voici la preuve que, peu importe où nous sommes en réalité, tout nous indique que nous sommes au centre de l'univers. Big_Bang_02_Doppler_Lorentz_Scan.avi Le programme : Big_Bang_02_Doppler_Lorentz_Scan.bas
Peu importe sa vitesse, l'observateur mesure le même "redshift" dans la lumière provenant des deux galaxies opposées voisines. En effet, l'effet Doppler relativiste n'est perceptible que selon la différence de vitesse, qui correspond ici à la vitesse alpha. Cet effet Doppler doit être relativiste, car autrement de nombreuses anomalies permettraient à l'observateur de détecter sa vitesse.
Le "théorème" montré ci-dessus fait appel aux propriétés remarquables des ondes stationnaires d'Ivanov. Il montre que la situation des observateurs B et D est équivalente sous les transformations de Lorentz. Il leur est tout à fait impossible de déterminer qui est le plus rapide à cause de la présence d'une constante dans leurs relevés. Il s'agit de la longueur d'onde mesurée, qui est étonnamment identique à la moyenne géométrique des deux longueurs d'onde. En effet, leurs mesures sont faussées à cause de la contraction de leur environnement, qui affecte aussi la longueur du mètre. L'animation suivante en est la preuve, car elle constitue une expérience de physique réalisée à l'aide d'un médium virtuel.
Les transformations transversales. Le 30 avril 2010, j'ai pu établir une version tridimensionnelle des transformations de Lorentz (voir plus bas). À
l'aide de ces équations, il devient possible
de montrer le déroulement du « Big Bang »: Le programme : Big_Bang_01_Relativistic.bas Désormais, les transformations de Lorentz peuvent s'appliquer à un espace cartésien en trois dimensions. Cet espace est absolu. Il n'est pas transformable, pas plus que le temps d'ailleurs. L'axe des abscisses n'est pas l'axe du déplacement comme on le croyait; c'est plutôt l'axe des transformations déterminé par les observateurs A, B et C montrés ci-dessus. La position de ces observateurs doit être établie selon une suite alpha (voir plus bas) pour que l'observateur B (qui se déplace à la vitesse alpha) puisse considérer que ses "jumeaux" A et C se déplacent en sens contraire et à la même distance. Puisque leur vitesse est la même selon B, ils ont le même temps et le même espace selon lui, ce qui démontre que la Relativité n'implique pas nécessairement une prétendue "transformation de l'espace-temps". D'une part, cela permet de lever une fois pour toute le célèbre paradoxe des jumeaux, ici A et C, qui peuvent alors concilier leurs observations apparemment opposées. D'autre part, si les jumeaux sont remplacés par des galaxies, on peut obtenir une représentation très convaincante d'un univers en expansion à la suite d'un hypothétique Big Bang, comme en font foi les animations présentées dans cette page. On sait que Lorentz avait donné: y' = y; z' = z. Ces grandeurs demeurent justifiées si le déplacement se fait effectivement sur l'axe des x et à petite échelle. Mais les équations données plus bas dans l'encadré sont obligatoires s'il faut transformer plus d'un objet dont la direction n'est pas la même. C'est également le cas s'il se produit une expansion. Alors les transformations comportent une composante y ou z comme c'est le cas pour l'observateur C' montré dans l'image ci-dessus. Le point important à retenir, c'est que l'observateur C utilise une horloge qui marque des heures plus lentes sur tout le plan orthogonal comprenant les axes y et z. En réalité, ce plan se déplace à la vitesse bêta et il faut donc ajouter cette vitesse à la composante Bêta(y) qui résulte du déplacement de C' sur l'axe y. Dans ce sens, l'axe des x est un axe privilégié où le temps absolu t s'applique alors que les axes y et z comportent des niveaux de transformation additionnels puisque ce sont plutôt des temps t[x]' et t[xy]' qui s'appliquent. Si l'on tient à ce que la vitesse absolue soit la même sur les deux axes x et y, il faut donc accélérer au préalable la vitesse sur l'axe transversal selon le facteur g qui a cours sur l'axe x. Bien évidemment, pour respecter la Relativité, la vitesse absolue doit être inférieure à celle de la lumière. Ce pourrait être jusqu'à 0,999 fois la vitesse de la lumière sur chacun des trois axes sans problèmes. Alors ces équations produiront malgré tout une composante de vitesse inférieure à celle de la lumière, de la même manière que le fait l'équation de Poincaré sur l'addition des vitesses relativistes. Je tiens à souligner que la formule y' = g * y + bêta * t' est calquée strictement sur la formule originale de Lorentz, mais en permutant les variables y, y' et t, t'. Il est plus raisonnable en effet d'attribuer les variables y' et t' au référentiel en mouvement. On sait que Lorentz appliquait ses transformations à l'électron en mouvement de manière à le remettre au repos, ce qui avait pour effet de rendre les équations de Maxwell invariantes quelle que soit la vitesse d'un référentiel. 1 – En intégrant la vitesse normalisée: bêta = v / c et le facteur de contraction: g = racine(1 – bêta ^ 2) pour simplifier comme le faisait Poincaré, voici la formule originale de Lorentz :
2 – On remplace l'axe x par l'axe y : y' = (y – bêta * t) / g 3 – On permute les variables y, y' et t, t' : y = (y' – bêta * t') / g 4 – Puis on extrait la variable y': y' = gy * y + bêtay * t' 5 – Si l'on échange les variables x et t avec x' et t', cette formule est donc la réplique exacte de celle que Lorentz avait établie pour l'axe x, c'est à dire avec le temps t' et non pas t. Par contre, l'ordinateur montre clairement que sur l'axe x, il faut utiliser le temps t et non pas t'. C'est tout aussi évident d'un point de vue logique puisque les mouvements de translation que nous observons selon nos mesures se font bien évidemment selon la transformation de Galilée: x' = x + bêta * t. Pas de doute, la formule correcte doit se lire : x' = g * x + bêta * t. En définitive, sur cet axe, il suffit donc d'inverser les variables x et x' dans les équations originales de Lorentz pour que l'ordinateur produise l'effet Doppler convenable (au lieu de le corriger, ce qui était l'intention initiale). Sans doute, Lorentz a confondu t et t', et cette erreur était déjà présente dans les équations initiales que Voigt avait élaborées vers 1887. Ainsi donc, avec le recul, on réalise que les variables x et t devraient s'appliquer impérativement au référentiel au repos puisque c'est le référentiel privilégié. Mais étonnamment, s'il faut transposer les équations de Lorentz dans un univers en trois dimensions, on trouve qu'il faut utiliser le temps t[x]' qui a cours pour une coordonnée x' donnée pour établir ensuite les grandeurs y'. En cascade, il faut finalement faire appel au temps t[xy]' pour établir ensuite les grandeurs z'. Cela tient au fait qu'il faut se référer à ce qu'un observateur situé à cet endroit voit sur tout le plan orthogonal dans lequel il se situe. On est alors en mesure de savoir la vitesse absolue d'une galaxie située en ce point et son temps t[xyz]', qui n'est pas vraiment le temps mais plutôt la période de l'onde en ce point. Voici donc les équations qui doivent s'appliquer dans un univers en trois dimensions, qu'il soit ou non en expansion :
Une nouveauté : les transformations tridimensionnelles tous azimuts. La formule x' = (x + bêta * t') / g est pratiquement identique à l'équation originale de Lorentz. Mais puisqu'on a t' et non pas t, elle montre que Lorentz a confondu ces variables. De plus, il est plus logique d'attribuer les variables x et t au repère fixe. Alors le facteur gamma peut être abandonné car le facteur de contraction g de Lorentz, qui est l'inverse, est le véritable facteur. La formule : gxyz = gx * gy * gz introduit une autre nouveauté : la loi de l'addition des composantes de vitesse. Henri Poincaré avait énoncé une loi similaire sur l'addition des vitesses selon laquelle la vitesse de la lumière ne peut être atteinte.
J'ai poli et repoli ces équations en mai et juin 2009 pour leur donner une beauté formelle qu'elles n'avaient pas au départ. Reproduite à l'aide de ces équations, même l'onde de phase découverte par Louis de Broglie se révèle remarquablement précise. Cela garantit que l'émetteur d'onde, qui doit faire appel à cette onde de phase, produira un effet Doppler pour ainsi dire parfait. D'ailleurs, je n'ai pas hésité à transformer Lorentz lui-même. C'est ce qu'on pourrait appeler la transformation de Lorentz ! Lorentz_3D_Transformations.mkv La contraction en particulier est évidente. Le but véritable était de montrer que l'onde de phase doit être associée à la contraction (il faut la situer dans une ellipse et non un cercle) pour qu'elle se superpose parfaitement à l'effet Doppler relativiste. Ces formules sont indispensables s'il faut afficher sur un même écran plusieurs structures ou émetteurs d'ondes dont la vitesse et la direction ne sont pas les mêmes. C'est le cas des animations proposées ici et dans lesquelles on peut voir des galaxies se déplacer et se contracter conformément aux indications de Lorentz. Mais il y a mieux: les mêmes équations permettent de programmer l'émetteur d'ondes. Cet émetteur est non seulement contracté comme les galaxies(x' = g * x) et déplacé (+ bêta * t) en fonction du temps écoulé, mais il présente une phase qui est modifiée à deux niveaux. Elle est d'abord ralentie selon le facteur g de Lorentz (t' = g * t) et elle accuse en plus un décalage horaire, ce "temps local" étant donné par: –bêta * x. Cela produit l'onde de phase dont il est question ici. Je tiens à répéter que la même onde de phase permet au Scanner du Temps de balayer une scène à la vitesse 1 / c, exprimée en secondes-lumière par seconde ou encore en longueurs d'onde par période d'onde. Cette onde de phase peut prendre diverses formes, comme en fait foi l'animation qui suit: Voici une représentation très détaillée et très précise de l'effet Doppler qui en résulte, un gros plan du cœur de l'émetteur, puisque c'est en définitive l'unique fonction des transformations de Lorentz: Et voici enfin la plus récente version de l'électron en mouvement, qui est fait d'ondes "stationnaires mobiles" sphériques. Je l'avais présenté dès l'an 2002 dans mon ouvrage "La matière est faite d'ondes" sous le nom "d'onde de La Frenière". Ici, grâce aux équations tridimensionnelles de Lorentz, il se déplace selon des composantes de vitesse x et y, donc sur une diagonale. Comme M. Jocelyn Marcotte l'avait découvert, on peut l'obtenir très simplement à partir du sinus cardinal, soit: y=sin(x)/x. Doppler_Moving_Electron_Diagonal.avi Doppler_Moving_Electron_Diagonal.bas Le programme disponible ci-dessus étant vraiment élémentaire, il montre que l'application de ces formules est d'une grande simplicité. Il faut toutefois garder à l'esprit que les coordonnées en pixels doivent être converties en longueurs d'onde. De la même manière, ce que Lorentz appelle le "temps" représente en réalité la période des ondes, et c'est pourquoi il faut convertir les variables t et t' en radians si l'on souhaite afficher les ondes correspondantes sur l'écran. On peut effectivement déterminer le temps en se référant à la période d'une certaine oscillation, comme les horloges au quartz le font depuis longtemps. Mais l'erreur à éviter, c'est de confondre période d'onde et temps. Il faut donc réaliser qu'on a franchement dérapé à partir de 1905 en prétendant qu'on avait affaire à un "ralentissement du temps" au lieu de convenir tout simplement que la lumière et les ondes radio émises dans un référentiel en mouvement devaient présenter un effet Doppler particulier caractérisé par un ralentissement de la fréquence. Il faut dire qu'on ignorait à l'époque que la matière présentait des propriétés ondulatoires. Or on le sait maintenant. Cela signifie que les transformations de Lorentz s'appliquent aussi à la matière. Lorsqu'un ensemble de matière (et tout particulièrement une galaxie dans un univers en expansion !) est en mouvement : 1 – Cet ensemble se contracte sur l'axe de son déplacement selon le facteur g de Lorentz. 2 – La séquence des événements s'y déroule plus lentement selon le facteur g de Lorentz. 3 – Les mécanismes qui causent ces événements accusent du retard à l'avant selon le "temps local" découvert par Lorentz. Une expérience cruciale. On se pose la question suivante : si des observateurs postés dans des stations spatiales faisaient en sorte de conserver entre eux une distance égale mais sans cesse croissante, existerait-il un moyen de détecter une anomalie dans l'effet Doppler qui résulterait d'un mouvement de l'ensemble dans un sens plutôt que dans l'autre ? La séquence ci-dessous prouve hors de tout doute que malgré l'effet Doppler, les tests se révèleront toujours négatifs. Big_Bang_04_Apparently_Equidistant.mkv C'est très clair : là encore, les tests que nous conduirons dans le futur à l'aide de véritables stations spatiales donneront à penser que nous sommes au centre de l'univers, puisque rien ne nous indique que nous sommes en mouvement. C'est dû au fait que l'effet Doppler "relativiste" semble toujours relatif, comme son nom l'indique, mais sans pourtant l'être vraiment dans l'absolu. Il peut révéler une différence de vitesse, mais il ne peut jamais révéler le mouvement de translation d'un ensemble, comme je l'ai déjà démontré, ni même des anomalies dans l'effet Doppler résultant d'une expansion continue, comme on le constate ici. Encore une fois, je vous propose aussi le programme qui a réalisé ces images. J'ai pris la peine de le soigner plus que d'ordinaire pour que vous puissiez vérifier que tout est dans l'ordre et que les formules utilisées correspondent bel et bien à celles qui sont indiquées plus haut. Big_Bang_04_Apparently_Equidistant.bas Or il y a mieux encore, puisqu'on peut confirmer le tout à l'aide du Scanner du temps. On a vu que l'observateur B est autorisé à penser qu'il est au repos et au centre de l'univers puisqu'il reçoit au même instant aussi bien les échos de son signal radio que l'accusé de réception des quatre observateurs orthogonaux A, C, D et E. Mais le Scanner peut aussi montrer ce que l'observateur C constate. En effet, ce dernier s'éloigne des ondes qui lui parviennent de l'arrière et il en résulte forcément une distorsion dans le temps. Il s'agit bien sûr du "temps local" découvert par Lorentz et dont parle abondamment Henri Poincaré. L'idée de base qui m'a conduit à mettre au point ce Scanner consistait justement à corriger cette distorsion de manière à montrer le point de vue de cet observateur mobile, mais j'ai pu constater à ma grande surprise que ce dispositif reproduisait en réalité les transformations de Lorentz dans leur ensemble, et pas seulement le temps local. Voici donc ce que l'observateur C devrait voir si l'on se fie au Scanner du Temps: Big_Bang_04_Apparently_Equidistant_Scan.mkv
Les transformations de Lorentz. Ce que voit l'observateur C, qui est à droite, est exactement l'inverse de ce que voit l'observateur A. Ces images montrent avec la plus grande clarté que, peu importe notre vitesse réelle, nous avons toujours l'impression d'être fixes. Peu importe notre position réelle, nous avons aussi l'impression d'être au centre de l'univers. Ce sont là les effets de la Relativité dans toute sa splendeur. Il en ressort que les transformations de Lorentz sont incontournables et qu'elles doivent s'appliquer aussi au Big Bang.
Ces formules sont magiques ! Un jour, on réalisera toute leur importance. Il ne sera pas possible de parler d'ondes, de mouvement, de champs de force, d'énergie cinétique, d'effet Doppler, d'astronomie, d'astrophysique ou de Relativité sans y avoir recours. Ces expériences montrent clairement que si notre univers était simplement en expansion (accélérée ou non) selon la constante de Hubble, nous pourrions détecter des anomalies selon la direction en examinant les galaxies éloignées. Nous pourrions en mesurant ces anomalies nous situer à l'intérieur de la sphère cosmique. Or ce n'est pas le cas: tout se passe comme si nous étions au centre. Les astronomes ont donc certainement tort de penser que le redshift inhabituel (c'est à dire supérieur à 2 selon 1 + bêta) peut être attribué sans problèmes à l'expansion de l'univers. Il est plutôt attribuable à l'effet Doppler relativiste tel que décrit par les transformations de Lorentz. L'explication bien connue du pudding aux raisins qui gonfle ne tient pas la route: elle est par trop simpliste pour rendre compte de ces phénomènes. Encore une fois, c'est Lorentz qui avait raison, avec en prime une explication plus raisonnable de l'anomalie dans la luminosité des supernovae constatée par M. Perlmutter (voir plus bas). Je dois encore évaluer la possibilité d'une expansion des galaxies elles-mêmes. Elle s'appliquerait en fait à tout notre environnement et elle se ferait dans les mêmes proportions que celle de l'Univers. Si c'était le cas, les galaxies les plus éloignées seraient plus petites, en proportion du facteur g. Il faudrait alors adapter ces formules à une telle situation. Mais ce n'est qu'une hypothèse. Elle apparaît vraisemblable, mais puisqu'il n'en existe à l'heure actuelle aucun indice, il vaut mieux la laisser en suspend. Une méprise de la part de Lorentz: t' et non pas t. Jusqu'à récemment, je n'arrivais pas à m'expliquer clairement pourquoi il fallait utiliser le temps t et non t' pour produire un effet Doppler correct lorsque le mouvement avait lieu sur l'axe des abscisses. J'en avais conclu que n'importe quel phénomène cyclique régulier, par exemple le mouvement de la terre autour du soleil, pouvait servir de référence absolue pour établir le temps, même s'il était relevé dans un autre référentiel. Il n'empêche qu'il faut utiliser impérativement t pour A et t' pour C puisque le calcul s'appuie sur l'existence de l'éther. La situation de ces jumeaux (c. f. le paradoxe des jumeaux) n'est pas réversible car l'observateur A voit les faits tels qu'ils se produisent vraiment. C et C' (ou D ci-dessus) sont au contraire victimes d'une mystification parce qu'ils subissent les transformations de Lorentz et qu'ils doivent composer avec l'effet Doppler relativiste, qui est particulièrement trompeur. Finalement, la véritable vitesse, la véritable contraction et la véritable période des ondes dans l'absolu. Considérant les trois axes, la composante des vitesses normalisées bêta[xyz] peut s'établir selon le théorème de Pythagore, mais il est plus simple de recourir au raccourci ci-dessous. Il faut noter que la vitesse réelle sur l'axe y et l'axe z s'en trouvera finalement ralentie. Ce calcul a l'avantage d'effectuer automatiquement la correction nécessaire pour éviter que la vitesse absolue n'atteigne ou ne dépasse la vitesse de la lumière, ce qui est une condition essentielle pour que la Relativité se vérifie. C'est ce qui me permet d'affirmer qu'il existe une loi des composantes de vitesse relativistes qui respecte cette condition essentielle: gxyz = gx * gy * gz ...ce qui permet de connaître la vitesse absolue correspondante : bêtaxyz = racine(1 – gxyz2) On peut finalement savoir l'heure t[xyz] plus lente qu'une horloge située sur cette galaxie affichera et qui convient à sa vitesse absolue bêta[xyz] et à ses coordonnées x', y' et z' comme le montre la dernière équation dans l'encadré ci-dessus. Après conversion en radians (multiplier par 2 * pi et diviser par la longueur d'onde), il s'agira tout aussi bien de la période qu'il faut appliquer à un émetteur d'ondes. On constate alors avec admiration que cette période suit l'onde de phase pressentie par Louis de Broglie, et dont la vitesse est toujours supérieure à celle de la lumière. Elle vaut en effet: 1 / bêta si elle est évaluée en secondes-lumière par seconde. Les animations proposées sur cette page démontrent que cela produit un effet Doppler parfait peu importe la vitesse ou la direction de l'émetteur. C'est une chose que je n'étais jamais arrivé à réaliser jusqu'à maintenant. Bref, ça fonctionne magnifiquement... Big_Bang_03_Multiple_Doppler.mkv Le programme FreeBASIC : Big_Bang_03_Multiple_Doppler.bas
Vous avez bien lu, dans les trois cas suivants, il faut recourir à ces mêmes équations tridimensionnelles: 1– Pour reproduire l'onde de phase dont parle de Broglie. 2– Pour programmer un effet Doppler relativiste au moyen du médium virtuel Delmotte-Marcotte. 3– Pour modifier la forme et la position des galaxies.
Voici un échantillon de ce que montre la séquence vidéo à l'aide du médium virtuel Delmotte-Marcotte. Ici, l'observateur B se déplace à la vitesse intermédiaire alpha, soit 0,5 c, sachant que C s'éloigne à 0,8 c. On notera avant tout que la longueur d'onde demeure constante dans les directions transversales. Cette invariance, qui est la caractéristique majeure des transformations de Lorentz, fait en sorte que la Relativité se vérifie. C'est dû au fait que la fréquence d'émission ralentit selon le facteur de Lorentz g, qui est l'inverse du facteur gamma. D'une part, les équations tridimensionnelles proposées plus haut permettent de réaliser un effet Doppler variable et tous azimuts. D'autre part, les mêmes équations permettent de déplacer et de contracter les petites ellipses blanches, qui représentent des galaxies. Cela signifie que la matière et les ondes se comportent strictement de la même manière !
La conclusion qu'il faut en tirer s'impose alors dans toute sa splendeur :
Le centre de l'univers. L'analogie bien connue du pudding aux raisins montre que chaque raisin conserve sa position relative à l'intérieur d'un certain volume, si celui-ci prend de l'expansion d'une manière linéaire. Du point de vue de chaque raisin, les autres s'éloignent d'autant plus rapidement que leur distance est grande. La constante de Hubble a été établie selon cette vision de notre univers en expansion, qui à première vue semble expliquer pourquoi il n'est pas possible de savoir où se situe le centre. Or c'est maintenant très clair : si l'univers se comportait de la sorte, les phénomènes optiques nous permettraient de déterminer notre vitesse et notre position comparativement au centre. En réalité, c'est à cause des transformations de Lorentz que nous avons l'impression d'être au centre de l'univers. C'est la conséquence la plus surprenante de la Relativité ! En voici la preuve irréfutable, réalisée grâce à mon Scanner du Temps : Big_Bang_01_Relativistic_Scan.mkv Le programme : Big_Bang_01_Relativistic_Scan.bas On voit bien que l'observateur B est transféré au centre de la sphère malgré le fait qu'en réalité, il se situe à mi-chemin entre le centre et la surface. Il ne voit pas d'effet Doppler dans les ondes qu'il émet mais il constate un effet Doppler égal pour les quatre échos qu'il reçoit de A, C, D et E en raison de l'expansion. Les galaxies lui apparaissent contractées en fonction de sa propre position et non pas celle de A. L'explication de ce phénomène a échappé à tous les scientifiques jusqu'à maintenant. Elle est pourtant d'une simplicité enfantine. Si nous sommes en mouvement, nous allons à la rencontre des ondes qui nous informent de la position des galaxies situées à l'avant. La scène que nous observons à l'avant s'est donc déroulée bien avant celle qui se situe à distance égale, mais à l'arrière. Le Scanner du temps peut tout aussi bien compenser ou reproduire cette distorsion. Ici il la reproduit, de sorte qu'il peut représenter ce que l'observateur B observe au point d'en être totalement mystifié. Tôt ou tard, les astrophysiciens devront donc admettre une fois pour toutes que la Relativité s'applique à tout en ce monde, et tout particulièrement à notre univers dans son ensemble. La sphère cosmique. Il se peut que tout prenne de l'expansion avec le temps. La Relativité serait respectée pour peu que les transformations tridimensionnelles de Lorentz soient respectées. Si l'univers est en expansion dans un éther fixe (c'est le point important), il doit absolument se conformer aux équations tridimensionnelles de Lorentz indiquées dans l'encadré ci-dessus. Mais puisque cette expansion est négligeable à petite échelle, même celle d'une galaxie, les équations y' = y; z' = z données par Lorentz s'appliquent la plupart du temps. C'est le cas en particulier de l'interféromètre de Michelson. Ce calcul indique que la surface de la sphère constitue un véritable "mur du temps" au-delà duquel aucune galaxie ne saurait exister puisque la matière ne peut dépasser ni même atteindre la vitesse de la lumière. La constante de Hubble se précisant d'année en année, on peut aujourd'hui avancer que le rayon de cette sphère, telle que nous la voyons, pourrait atteindre 14 milliards d'années-lumière. Ce pourrait être le double en tenant compte du fait que les galaxies les plus éloignées étaient déjà situées à cette distance il y a 14 milliards d'années, au moment où elles ont émis leur lumière. Ce pourrait même être bien davantage si l'univers était en expansion accélérée, ou si nous étions situés malencontreusement tout près de cette surface. J'ai déjà montré qu'il existe une suite mathématique qui permet de concilier ces observations avec les principes les plus élémentaires de la Relativité, c'est à dire la contraction, le décalage horaire et le ralentissement des horloges. Je l'ai nommée la "suite alpha" puisqu'elle est basée sur la vitesse intermédiaire "alpha", le calcul étant fondé sur la loi de l'addition des vitesses relativistes élaborée par Henri Poincaré. Bien évidemment, les galaxies ne sont pas disposées avec une pareille régularité, mais leur distribution au hasard et tous azimuts doit se conformer à l'allure générale de cette suite. Le but est de démontrer que si des galaxies (ou des stations spatiales bien plus lentes, par exemple) sont disposées selon cette suite, des observateurs postés dans chacune d'elles auront l'impression que la précédente et la suivante se déplacent en sens opposé à la même vitesse et qu'elles sont situées à la même distance. Non seulement cela peut se vérifier expérimentalement, mais c'est aussi ce que montre un calcul élémentaire tenant compte de l'effet Doppler. Ainsi donc, cette représentation met en évidence une vitesse intermédiaire alpha que j'ai découverte en 2009 et qui permet de concilier les observations de deux autres observateurs dont l'un est au repos et l'autre en mouvement. alpha = (1 – g) / bêta
Le calcul est basé sur la loi de l'addition des vitesses relativistes de Poincaré : bêta' = (alpha + bêta) / (1 + alpha * bêta) bêta = 2 * alpha / (1 + alpha ^ 2) Personne ne semble avoir proposé la soustraction correspondante : bêta = (bêta' – alpha) / (1 – alpha * bêta') Il s'agit d'une méthode permettant d'expliquer beaucoup mieux le paradoxe des jumeaux. Je n'ai découvert la suite correspondante qu'en avril 2010. Puisqu'il s'agit d'une suite, on peut désormais mettre en scène plus de deux jumeaux. On pourrait parler par exemple du paradoxe des septuplés (A à G ci-dessus), que la Relativité de Lorentz permet d'expliquer sans peine. Par exemple, s'ils sont observés par E, les jumeaux C et G semblent se situer à la même distance et s'éloigner en sens opposé à la même vitesse, soit bêta = 0,5 fois la vitesse de la lumière. La galaxie C est contractée selon le facteur g = 0,866 prévu par Lorentz. Sa lumière subit l'effet Doppler normal mais il s'y ajoute un "redshift" relativiste correspondant à ce même facteur g. Cet effet Doppler additionnel est attribué de nos jours à l'expansion de l'univers mais il s'apparente en réalité au ralentissement des horloges et donc à la fréquence des émetteurs. Il a été découvert par Voigt en 1887 et quantifié par Lorentz en 1904. De la même manière, le jumeau C voit les jumeaux B et D s'éloigner à la vitesse alpha = 0,2679 fois la vitesse de la lumière et ses instruments lui indiquent (mais c'est inexact) qu'ils sont situés à la même distance. Cela explique pourquoi, peu importe où nous sommes à l'intérieur de cette sphère, nous avons l'impression d'être au centre de l'univers, ce qui est bien évidemment improbable. La vitesse de référence alpha de départ est facultative. Plus elle est faible, plus il faut d'accélérations successives correspondant à cette vitesse pour atteindre une vitesse quelconque dans la suite alpha. Il s'agit bien sûr d'une accélération relativiste, de sorte que même des milliers d'accélérations successives ne permettent jamais d'atteindre la vitesse de la lumière. Voici trois preuves. Pour vérifier cette hypothèse, nous ferons donc appel à cette vitesse de référence intermédiaire, que j'ai nommée "alpha", puisqu'elle est toujours inférieure à une vitesse normalisée bêta quelconque, fixée arbitrairement. J'ai déjà présenté trois preuves de la pertinence d'une telle vitesse de référence, dont l'avantage principal est de ne plus avoir à invoquer une transformation de l'espace et du temps pour expliquer la Relativité. Il faut plutôt invoquer, comme l'a fait Lorentz, une contraction de la matière, un décalage horaire et un ralentissement de la fréquence de tous les phénomènes cycliques. Un tel ralentissement affecte en particulier les heures affichées par les horloges, la fréquence des ondes qui constituent l'électron et celle des ondes de la lumière, dans tout le spectre allant des ondes kilométriques aux rayons gamma. Mais il affecte aussi tous les mécanismes matériels, par exemple les orbites des planètes. Cela signifie que si tout notre système solaire était accéléré à 86,6% de la vitesse de la lumière, les années dureraient deux fois plus longtemps et tout le système planétaire serait contracté de moitié sans que nous ayons la possibilité de nous en rendre compte. N'allez pas croire qu'une telle contraction devrait entraîner des contraintes mécaniques intolérables, comme on l'a fait remarquer parfois. Cela se produit précisément pour des raisons mécaniques, toutes les forces mises en jeu (qui sont attribuables à des ondes) subissant elles-mêmes les transformations de Lorentz puisqu'il s'agit purement et simplement d'un effet Doppler. La première preuve montre que le recours à une telle vitesse alpha permet de produire un effet Doppler parfait à l'aide de mon Scanner du Temps tout en conservant les mêmes grandeurs x et y d'un référentiel cartésien. L'animation proposée plus haut (Cosmic_Sphere.mkv) vient encore étayer cette preuve en la généralisant puisqu'elle montre des objets subissant tout un éventail de transformations dans un même espace cartésien dont les coordonnées x, y et z demeurent invariables.
Voici une vidéo qui montre ce phénomène avec plus de précision : Time_Scanner_Doppler.mkv Vous pouvez aussi examiner le programme FreeBASIC qui a produit ces images : Time_Scanner_Doppler.bas Il faut observer que selon Lorentz, la longueur d'onde ne varie pas sur un axe transversal : x' = x; z' = z. Cette invariance transversale est fondamentale.
La deuxième preuve montre que les ondes stationnaires formées par les ondes provenant de deux électrons, l'un au repos et l'autre en mouvement semblent s'immobiliser aux yeux de l'observateur intermédiaire alpha. On présume ici que les électrons émettent des ondes qui subissent l'effet Doppler selon les transformations de Lorentz, ce qui est une hypothèse vraisemblable puisqu'on sait depuis longtemps que les particules qui composent la matière présentent des propriétés ondulatoires. Le programme FreeBASIC : Alpha_Field_of_Force.5c.bas La troisième preuve montre qu'il est possible d'effectuer une transposition de ces galaxies de manière à remplacer la galaxie centrale par la galaxie voisine, qui apparaîtra à son tour au centre, mais toujours en conservant scrupuleusement les mêmes coordonnées cartésiennes x et y. Peu importe leur vitesse propre, toutes les autres galaxies sont aussi transformées en conséquence. On peut constater qu'après transformation (le Scanner du Temps reproduit les transformations de Lorentz), la contraction selon un facteur de 0,866 et le décalage horaire de 5 secondes passent du système BB' au système AA'. On peut voir ci-dessous les deux systèmes avant et après les transformations de Lorentz.
Les transformations de Lorentz (bêta = 0,5; alpha = 0,2679). À gauche, on privilégie les observateurs A et A' et ce sont B et B' qui subissent les transformations. À droite, le Scanner du Temps a annulé les transformations subies par B et B'. Mais en même temps, il montre que les observateurs A et A' ont subi à leur tour les transformations de Lorentz. À noter que l'observateur alpha ne subit aucune transformation, pas plus que l'échelle des grandeurs x et y. Cela signifie que l'espace et le temps ne se transforment pas et que la vitesse de la lumière dépend de l'éther.
Encore une fois, l'animation proposée plus haut (Cosmic_Sphere.mkv) vient étayer cette preuve puisque le Scanner du Temps réussit l'exploit de représenter tous les observateurs de telle manière que c'est l'observateur C qui se retrouve au "Centre Cosmique" après le balayage. L'observateur Alpha est en mesure de concilier les observations de ces deux acteurs A et C. Toute la magie de la Relativité est respectée scrupuleusement, de sorte que personne ne peut savoir où se situait le point exact de l'explosion lors du Big Bang comparativement à nous. Il faut souligner que vers 1905, tous les physiciens (en particulier Lorentz, Poincaré et Einstein) auraient été parfaitement d'accord avec ce modèle de sphère cosmique puisqu'il respecte les fondements les plus élémentaires de la Relativité. Toutefois, il aurait fallu au préalable les informer de l'existence de telles galaxies, et surtout du fait qu'elles s'éloignent les unes des autres comme Edwin Hubble l'a découvert. Les physiciens vivant à l'époque de Hubble (y compris Einstein lui-même, qui a donc trahi sa Relativité restreinte) furent donc confrontés à un problème nouveau qu'ils n'ont pas su résoudre correctement. Le but de la physique n'est pas seulement de prévoir les phénomènes à l'aide d'équations et de principes. Il ne faut jamais perdre de vue que les phénomènes physiques ont des causes mécaniques, et qu'il est beaucoup plus facile de prévoir les effets si on connaît les causes. Or Lorentz avait déjà réussi à les identifier, et il aurait donc fallu se référer à sa version de la Relativité, qui est d'ailleurs beaucoup plus simple et logique. L'univers n'est pas nécessairement en expansion accélérée. Je me permets donc de remettre en question les conclusions de nombreux astrophysiciens qui, apparemment, n'ont rien compris à la Relativité. En particulier, M. Saul Perlmutter me semble un peu pressé d'affirmer que l'univers est en expansion accélérée. Je ne conteste pas l'importance de sa découverte. Elle est en effet d'une importante capitale et sa conclusion pourrait d'ailleurs s'avérer tout à fait juste. C'est plutôt son raisonnement qui me semble suspect. J'ai eu l'occasion de le voir expliquer sa thèse sur le réseau PBS américain puisque celui-ci peut être capté au sud du Québec en haute définition à l'aide d'une simple antenne UHF. Il s'appuie principalement sur le fait que la luminosité des supernovae du type Ia est constante. Les chiffres que lui et son collaborateur ont relevés s'écartent en effet de ce qu'on devrait obtenir compte tenu de la constante de Hubble. Je pense en toute objectivité que le problème comporte trop d'inconnues pour qu'il ait le droit d'en tirer des conclusions avec autant d'assurance. Le problème, c'est qu'il considère que les galaxies très éloignées et donc très rapides ne subissent pas les transformations de Lorentz. Il faudrait d'abord tenir compte de la Relativité la plus élémentaire avant de songer à une expansion accélérée qui viendrait compliquer encore le calcul. Pour l'instant, il vaut mieux penser que c'est plutôt la constante de Hubble qui n'est pas vraiment constante. La courbe doit s'incurver lorsque la supernova (dont on doit mesurer la luminosité compte tenu de l'effet Doppler relativiste) se déplace à une vitesse qui n'est plus négligeable comparativement à celle de la lumière. Voici un graphique qui montre un écart significatif entre la luminosité d'une supernova, selon qu'on considère (courbe rouge) ou non (courbe verte) les transformations de Lorentz:
Ces courbes ne représentent qu'une possibilité parmi d'autres. Il existe de nombreuses incertitudes. On remarque en particulier que l'effet Doppler relativiste atteint une valeur de 2 à 0,6 fois (g = 0,8) la vitesse de la lumière: (1 + 0,6) / 0,8 = 2. Or si la Relativité ne s'applique pas, cette valeur n'est atteinte que si un corps céleste atteint exactement la vitesse de la lumière, soit selon: 1 + bêta = 2. On peut penser que l'explosion d'une supernova provoque l'éjection de particules de matière lumineuse à des vitesses relativistes, d'où un redshift moins sévère. Il faudrait même s'assurer que la constante de Hubble est vraiment constante. Bref, il est très possible que l'univers soit effectivement en expansion accélérée, mais c'est à voir. Jusqu'à preuve du contraire, il vaut mieux penser que la vitesse des galaxies éloignées est constante. Si donc le redshift est relativiste, il n'est plus possible de penser que si une galaxie dépasse le seuil critique de 2, sa vitesse est forcément supérieure à celle de la lumière. On prétend à l'heure actuelle qu'elle continue d'être au repos dans son "espace" puisque c'est l'espace lui-même qui prend de l'expansion. Il faudra donc corriger la vitesse des galaxies les plus éloignées pour qu'elles ne dépassent jamais la vitesse de la lumière. Par exemple, un redshift de 100 dans la lumière d'une galaxie indiquerait que sa vitesse vaut 0,9998 fois la vitesse de la lumière. Dans ces conditions, on constatera que les galaxies sont d'autant plus serrées les unes sur les autres que leur vitesse approche celle de la lumière, de manière à respecter la contraction prévue par Lorentz. Il faut tenir compte de la contraction et du ralentissement des horloges. Ce que la constante de Hubble nous indique, c'est que plus les galaxies sont rapides, plus elles sont éloignées. Et puisqu'il s'agit d'une constante, la progression est linéaire et non pas exponentielle. C'est pourquoi la suite alpha que je propose respecte une échelle des vitesses normalisées bêta qui est strictement linéaire correspondant à des distances distribuées également de manière linéaire, la moitié du rayon correspondant (vraisemblablement) à 7 milliards d'années-lumière là où la vitesse atteint la moitié de la vitesse de la lumière. Toutefois, et c'est le point important, il faut se rappeler que Lorentz et Einstein ont bien indiqué que plus les objets se déplacent rapidement, plus ils nous apparaissent contractés. On en voudra pour exemple le paradoxe du train et du tunnel: du point de vue d'un observateur posté dans un tunnel, dont la longueur serait la même que celle du train immobilisé dans ce tunnel, ce même train lui apparaîtrait plus court s'il traversait le tunnel à grande vitesse. Mais s'il y a plusieurs trains qui se suivent à des vitesses et à des distances respectant la constante de Hubble, on fait face à un problème additionnel parce que ces distances elles-mêmes se contractent. Selon Lorentz, cela se produit pour des raisons mécaniques alors que selon Einstein, c'est l'espace lui-même qui se contracte. Mais cela revient au même en ce qui concerne les mesures effectuées par ceux qui observent les trains ou le tunnel. La courbe qui en rend compte s'incurve donc d'une manière exponentielle. La conclusion la plus évidente qu'on peut en tirer, c'est que plus la distance est grande, plus on devrait trouver de galaxies par unité de volume. Leur nombre serait relativement limité entre 2 et 3 milliards d'années- lumière, mais il serait théoriquement infini entre 13 et 14 milliards (en supposant que ce dernier chiffre corresponde à la vitesse de la lumière). Par ailleurs, Lorentz a aussi indiqué que tous les phénomènes se déroulent plus lentement dans un système qui se déplace à grande vitesse. C'est le cas de la lumière que les galaxies, les quasars ou les supernovae très rapides émettent. Non seulement leur vitesse impose l'effet Doppler classique vers l'arrière selon 1 + bêta, mais la fréquence d'émission ralentit de telle sorte que la longueur d'onde s'allonge encore davantage selon le facteur de Lorentz, soit g = racine(1 – bêta^2) : lambda' = lambda * (1 + bêta) / g Selon Lorentz, lorsqu'une galaxie s'éloigne à 0,6 fois la vitesse de la lumière (g = 0,8), nous voyons la longueur d'onde de sa lumière doubler exactement (1 + 0,6)/0,8 = 2. Cela devrait donc se produire si sa distance correspond à 8,4 milliards d'années-lumière. Les galaxies plus rapides peuvent donc dépasser largement ce seuil sans pour autant atteindre la vitesse de la lumière, alors qu'une simple expansion de l'univers ne peut pas produire d'effet Doppler relativiste. Il faudrait qu'une galaxie dépasse la vitesse de la lumière pour que ce seuil critique de 2 soit dépassé. Or on a effectivement relevé des redshifts supérieurs à 2 et Einstein lui-même n'a pas donné d'explication claire à ce propos. D'après la Relativité restreinte, si la "dilatation du temps" s'applique, la "contraction de l'espace" s'applique aussi mais cela compromet la théorie de Hubble, "l'espace" subissant à la fois une contraction et une expansion... La Relativité telle qu'énoncée dès 1904 par Lorentz et Poincaré rend au contraire parfaitement compte de ces phénomènes. Avant de parler avec conviction d'une expansion accélérée de l'univers et même de la présence "d'énergie noire", les astronomes devraient réaliser qu'il existe plus d'une hypothèse et qu'il est prématuré de n'en retenir qu'une seule. Il est très possible que l'univers ne soit pas en expansion accélérée et que ce soit tout simplement l'effet Doppler relativiste selon Lorentz qui produise l'effet découvert par M. Perlmutter. Il existe même un possibilité que l'univers ne soit pas en expansion du tout, bien que cette hypothèse soit très difficile à soutenir. De toutes façons, il n'est pas du tout certain que la lumière faiblisse à coup sûr selon la loi du carré de la distance sur de pareilles distances. Par exemple, mon hypothèse veut que l'électron soit amplifié par les ondes qui circulent dans l'éther. Cela suppose que chaque fois que la lumière traverse des particules interstellaires, elle en est affaiblie. La suite alpha. Seule, une suite alpha permet d'expliquer pour quelle raison un observateur donné voit deux galaxies situées à la même distance s'éloigner à la même vitesse relative mais dans deux directions opposées, peu importe leur vitesse réelle. C'est en observant le mouvement des deux émetteurs montrés plus haut (Alpha_Field_of_Force.5c.mkv), qui n'est pas tout à fait symétrique, que j'ai pu la préciser. Il a fallu recourir à la fois à la loi de l'addition des vitesses relativistes de Poincaré, au médium virtuel Delmotte-Marcotte et à mon Scanner du Temps pour la mettre en évidence. Elle respecte la Relativité d'Einstein, mais seule la Relativité selon Lorentz permet de l'expliquer. On sait que ces deux théories conduisent la plupart du temps (mais pas toujours) aux mêmes conclusions malgré le fait que les approches soient diamétralement opposées. La suite proposée ici est bien sûr arbitraire puisque n'importe quelle vitesse alpha et bêta de départ convient. De plus, bien évidemment, les galaxies ne respectent pas cette suite. Le but est de mettre en scène des observateurs de telle manière que chacun d'eux puisse se croire au centre de l'univers et de le vérifier. Or c'est maintenant possible grâce aux transformations tridimensionnelles de Lorentz et au médium virtuel Delmotte-Marcotte. La distance de base apparente entre chaque galaxie, à mesurer en milliards d'années-lumière, dépend de la date et de l'intensité du Big Bang, sachant que les galaxies qui se déplacent présentement à la moitié de la vitesse de la lumière ont dû accélérer progressivement jusqu'à atteindre cette vitesse. En pratique, le problème est plus simple et consiste à faire en sorte qu'un observateur posté dans une galaxie quelconque ait l'impression que si deux galaxies situées de part et d'autre semblent s'éloigner à la même vitesse, leur distance semble aussi la même. Ici, la suite est basée sur une vitesse bêta égale à la moitié de celle de la lumière, ce qui permet de retenir les chiffres plus simples et plus évocateurs de 0,8 et 0,5. bêta = v / c = sin thêta = 0,5 thêta = arc sin(v / c) = 30° g = racine(1 – bêta ^2) = cos thêta = 0,866 alpha = (1 – g) / bêta = (1 – cos thêta) / sin thêta = 0,267949192 Il faut ensuite recourir à la loi de l'addition des vitesses relativistes élaborée par Henri Poincaré pour établir la suite : bêta' = (alpha + bêta) / (1 + alpha * bêta) = 0,6772 bêta'' = (alpha + bêta') / (1 + alpha * bêta') = 0,8 bêta''' = (alpha + bêta'') / (1 + alpha * bêta'') = 0,8794 Inversement, on peut invoquer la "loi de la soustraction des vitesses relativistes" si l'on souhaite revenir en arrière : bêta = (bêta' – alpha) / (1 – alpha * bêta') = 0,5 Toute suite alpha s'étendant à l'infini, il est clair que l'âge de l'univers ne peut être déterminé. Ceux qui le situent vers 14 milliards d'années (ou le double) n'ont rien compris aux transformations de Lorentz ni à la Relativité, mais ce chiffre constitue néanmoins un minimum, un seuil au dessous duquel on ne peut descendre. Une galaxie qui s'éloigne à la moitié de la vitesse de la lumière et qui présente donc selon Lorentz un redshift combiné de: (1 + 0,5) / 0,866, soit lambda' = lambda * 1,732 se situe vraisemblablement à 7 milliards d'années lumière. Mais elle a beaucoup plus que 7 milliards d'années d'âge si elle a accéléré progressivement jusqu'à cette vitesse, à plus forte raison si elle continue d'accélérer. Il faut réaliser qu'il faut deux fois plus d'énergie et de temps pour accélérer une galaxie dont la vitesse initiale vaut 0,866 jusqu'à la vitesse de 0,9682 (g = 0,25; facteur gamma: 4) que pour accélérer la galaxie équivalente de zéro à 0,866 (g = 0,5; gamma = 2). Cela suppose des quantités d'énergie phénoménales, pour ne pas dire inexplicables. Pendant le temps que dura cette accélération peu après un hypothétique Big Bang, la lumière de l'explosion initiale aura eu le temps de se propager bien au-delà de la surface de la sphère cosmique, et elle seule pourrait nous dire l'âge de l'univers. Or cette lumière est inaccessible. La Relativité appliquée aux galaxies. C'est donc ce qui explique que l'observateur situé dans la galaxie B constate (à tort) que les galaxies A et C sont situées à la même distance et qu'elles s'éloignent toutes les deux en sens inverse et à la moitié de la vitesse de la lumière. Cet observateur est en effet aux prises avec des horloges plus lentes selon un facteur g de 0,866. Ces horloges présentent un décalage horaire de 0,5 milliards d'années lentes (selon: –bêta * x) pour chaque unité x d'un milliard d'années-lumière avant contraction, soit 0,866 milliards d'années dans les faits. Si la galaxie C semble à 3,75 milliards d'années-lumière aux yeux de B, bien plus loin que sa distance réelle (3,25 milliards), elle aura eu en réalité le temps de parcourir l'espace additionnel nécessaire pour que sa lumière atteigne B en même temps que celle provenant de A, sachant que la lumière provenant de l'arrière est trois fois plus lente que celle qui provient de l'avant: (1 + bêta) / (1 – bêta) = 3. Étant au repos comparativement à l'éther, seul l'observateur A peut le savoir à coup sûr car il n'est pas victime d'une mystification attribuable à l'effet Doppler et aux transformations de Lorentz. Le problème, c'est qu'il ne peut pas vérifier qu'il est véritablement au repos. Sa situation est donc tout aussi confuse que celle des autres observateurs. Pour ma part, je crois fortement à l'existence de l'éther. Tous ces phénomènes s'expliquent en effet d'une manière étonnamment simple en postulant que l'éther existe et que la vitesse de la lumière en dépend. C'est d'ailleurs ce que croyait Lorentz. Je suis donc parfaitement d'accord avec sa vision de la Relativité, qui fut publiée en 1904 et rapportée à partir de 1901 par Henri Poincaré avec force détails, hélas en y incorporant des dérapages regrettables de son crû. Mais d'un autre côté, je suis persuadé que cette contraction de la matière en mouvement doit être attribuée à la contraction des ondes stationnaires dont elle est faite, parce qu'elles subissent l'effet Doppler. Lorentz étant né bien avant Louis de Broglie, il ne pouvait pas le savoir. Il ignorait également que notre univers était fait de galaxies en expansion. Il ignorait surtout que cet "électron", qui selon lui se contractait, pouvait tout aussi bien être un proton ou n'importe quelle particule chargée. La vérité, c'est que si les ensembles formés d'électrons et de protons se contractent, la matière aussi doit se contracter. Pas l'espace, comme l'a prétendu ensuite Einstein. Peu importe la sphère cosmique envisagée, il est plus que probable que plus nos télescopes seront grands et précis, plus nous découvrirons d'autres galaxies dont la distance et la vitesse seront encore plus grandes. Il existe toutefois une limite matérielle. En effet, même des rayons X très puissants émis par une galaxie dont la vitesse (apparente ou relative) approche celle de la lumière deviennent à la limite trop faibles pour être détectés en raison d'un redshift considérable, qu'il soit relativiste ou "expansionniste".
UNE HYPOTHÈSE SÉDUISANTE : L'EXPANSION DE L'ÉTHER. LA RELATIVITÉ DE L'EXPANSION Je doute de plus en plus que de telles accélérations de galaxies entières, en nombre quasi infini et frôlant en grand nombre la vitesse de la lumière, soient possibles. Il faudrait faire intervenir tellement d'énergie qu'on ne peut même pas concevoir comment elle aurait pu être stockée. Je suis beaucoup plus tenté qu'autrefois de croire que c'est l'éther lui-même qui est en expansion à cause de son élasticité et que toutes les galaxies, même les plus éloignées, sont tout simplement au repos ou presque comparativement à l'éther local. Si ce devait être le cas, les galaxies seraient distribuées plus simplement au hasard, d'une manière linéaire et non pas exponentielle. Puisqu'il n'y a pas de limites théoriques, elles pourraient se situer à des distances inimaginables et s'éloigner de nous à des vitesses bien supérieures à celle de la lumière. La sphère cosmique montrée plus haut ne serait alors que le résultat d'une illusion, mais elle correspondrait pourtant bel et bien à ce que nous observons. Il faut donc reconnaître que M. Perlmutter et tous les astronomes qui considèrent que le redshift des galaxies éloignées est le résultat de "l'expansion de l'univers", qu'elle soit accélérée ou non, n'ont pas nécessairement tort. Ces sont plutôt les raisons qu'ils invoquent qui ne résistent pas à l'analyse. Voyons cela. L'effet Doppler et l'expansion de l'univers. Manifestement, l'expansion de l'univers, telle que les astronomes la conçoivent aujourd'hui, ne peut pas provoquer d'effet Doppler véritable. Les ondes émises par les galaxies éloignées, qui sont au repos dans leur "espace" local, devraient en effet demeurer sphériques et concentriques. C'est plutôt la vitesse relative de chacun des fronts d'onde qui devrait accélérer progressivement selon leur distance de l'émetteur, et donc selon le temps écoulé. En supposant que la longueur des ondes demeure constante lors de leur émission, cette longueur s'en trouverait augmentée progressivement. Près de l'émetteur, elles seraient alors plus courtes en comparaison. Le problème, c'est que nous observons bel et bien un redshift. C'est certainement parce que l'un des paramètres impliqués dans le processus ne varie pas en proportion de l'expansion. Par exemple, les dimensions des atomes et des objets matériels pourraient demeurer inchangées, ou ne pas correspondre exactement à l'expansion. Il pourrait aussi s'agir de la vitesse de la lumière, de la puissance des forces mécaniques ou encore de l'inertie de la matière. On peut même envisager une combinaison de ces différents paramètres. On prétend aujourd'hui que la taille de chaque galaxie ne varie pas malgré l'expansion de l'univers. Bien que cette hypothèse ne soit guère vraisemblable dans un tel contexte, elle a au moins le mérite d'expliquer pourquoi nous observons un redshift dans la lumière des galaxies éloignées. Nous allons donc vérifier pourquoi. Ci-dessous, la galaxie A est au repos comparativement aux coordonnées du diagramme lui-même. La galaxie B s'éloigne vers la droite à la vitesse de la lumière comparativement à A, mais elle est au repos comparativement au médium qui véhicule les ondes (que ce soit l'espace ou l'éther). Puisque ce dernier prend de l'expansion, chacune de ses parties s'éloigne du point A d'autant plus vite qu'elle en est éloignée. On présume aussi que la vitesse de la lumière est constante. C'est ainsi que la courbe verte extérieure représente un front d'onde qui s'éloigne de A à la vitesse de la lumière, plus une autre fois la vitesse de la lumière à cause de l'expansion. Si on suppose que cette onde a été émise il y a 14 milliards d'années (ce n'est qu'une hypothèse), elle s'éloigne en définitive à deux fois la vitesse de la lumière comparativement à A, mais bien évidemment à la vitesse de la lumière seulement comparativement à B à l'instant où elle l'atteint. À ce moment, la longueur d'onde a doublé à cause de l'expansion, d'où un redshift qui est mesurable si les dimensions de B n'ont pas changé, mais qui n'est plus mesurable si elles ont doublé.
Si tout ce que contient l'univers prend de l'expansion, tout se passe comme si cette expansion n'avait pas lieu. Les ondes émises dans un univers en expansion demeurent sphériques et concentriques : il n'y a pas d'effet Doppler.
La Relativité de l'expansion. Dans le cas où tous les objets de l'univers prennent de l'expansion, et pas seulement les galaxies, on peut donc parler fort à propos d'une "Relativité de l'expansion" puisque tout se passe comme si cette expansion n'avait pas lieu. Ce principe pourrait s'énoncer ainsi:
La Relativité de l'expansion.
Malgré sa grande simplicité, cette nouvelle Relativité n'a semble-t-il jamais été analysée correctement à ce jour. On aurait dû pourtant le faire dans les années qui ont suivi la découverte de Hubble puisque c'est à cette époque qu'on a commencé à parler de "l'expansion de l'univers" au lieu de parler plus simplement de la vitesse d'éloignement des galaxies. J'ai toutes les raisons de penser qu'on a fait ce choix parce que personne ne comprend la Relativité. On aura préféré éviter de tenir compte des transformations de Lorentz car cela aurait conduit au "Big Bang relativiste" tel qu'il est décrit dans cette page. Mais supposons que c'est plutôt l'éther (ou "l'espace", si vous y tenez) qui prend de l'expansion. Puisque c'est la théorie généralement admise aujourd'hui, il importe d'en établir les paramètres d'une manière plus rigoureuse puisque personne n'a encore osé le faire. Ce qu'il faut réaliser ici, c'est que nous avons pu constater que l'univers était effectivement en expansion (apparemment, en tous cas) puisqu'il se produit bel et bien un redshift. La Relativité de l'expansion, selon laquelle cette expansion serait invérifiable, ne constitue donc que la première étape de notre approche, qui nous servira de référence. Il s'agit ensuite d'en modifier certains paramètres de manière à déterminer plus facilement pour quelle raison le redshift des galaxies éloignées est apparent alors qu'il aurait pu tout aussi bien ne pas l'être. Il faut souligner dès le départ qu'une galaxie qui s'éloigne de nous à la vitesse de la lumière ne peut produire qu'un redshift mesurant deux fois la longueur d'onde normale, et pas plus, soit selon 1 + bêta. Logiquement, il faut que sa vitesse dépasse celle de la lumière comparativement à nous pour justifier un redshift supérieur à deux. Selon cette Relativité, le redshift est identique à celui de l'effet Doppler acoustique normal et il ne peut donc pas être "relativiste" dans le sens établi par Lorentz. Considérons un observateur qui se réveille un bon matin et qui constate que sa taille a doublé. C'est en tous cas ce qui semble s'être produit puisque sa maison lui apparaît maintenant deux fois plus petite. En toute relativité, il pourra tout aussi bien penser que c'est plutôt sa maison qui a rétréci. Mais si les dimensions de sa maison avaient également doublé, il ne pourra constater le changement qu'après avoir regardé dehors. En fait, si les dimensions de tout l'univers avaient doublé, il ne pourrait plus se rabattre que sur certains indices résiduels pour en faire la preuve. Par exemple, on sait qu'à gravité constante, la période d'oscillation du pendule est inversement proportionnelle au carré de sa longueur. Si l'expansion double sa longueur, il faudrait donc que la force de la gravité ait doublé ou encore que l'inertie de la matière ait diminué de moitié pour que la durée de sa période ait seulement doublé. Il s'agit en effet de concilier cette période avec le temps que met la lumière pour effectuer un aller et retour sur un trajet donné. Autrement, toujours en supposant que la vitesse de la lumière demeure constante, l'observateur pourrait détecter une anomalie en les comparant et calculer la valeur de son expansion. L'observateur peut aussi vérifier sa situation à l'aide d'un dipôle demi-onde émettant, disons, sur la bande d'un mètre. On sait qu'à cause des effets de capacité, ce dipôle doit mesurer un peu moins de 50 cm. Si sa longueur augmente jusqu'à atteindre un peu moins d'un mètre, il émettra sur une longueur d'onde de deux mètres de telle sorte que la longueur d'onde semblera inchangée aux yeux de notre observateur. Cela suppose encore une fois que la vitesse de la lumière demeure constante. Or en pareil cas, il ne pourrait absolument pas détecter de redshift dans la lumière des galaxies les plus éloignées. C'est dû au fait que l'expansion de l'éther aura fait en sorte que la longueur des ondes émises il y a près de 14 des milliards d'années aura également doublé. La Relativité de l'expansion implique donc une expansion des galaxies elles-mêmes et de tout ce qu'elles contiennent, c'est à dire la matière, les molécules, les atomes et leurs électrons. Elle implique une expansion de la longueur d'onde de l'électron lui-même et donc un ralentissement de sa fréquence. Toujours en supposant que la vitesse de la lumière demeure constante, cela ne peut conduire qu'à une sorte de "ralentissement du temps", qui serait tout aussi invérifiable. Bien évidemment, on devrait parler plutôt d'un ralentissement de tous les processus physiques puisque le temps en soi n'existe pas et ne peut donc pas ralentir. En réalité, c'est dû tout simplement au fait que si la longueur des ondes est doublée, leur fréquence et donc leurs actions ou leurs effets sont ralentis de moitié. De plus, toutes choses étant égales d'ailleurs, l'énergie d'une onde est proportionnelle à sa fréquence. Cela donne à penser que toutes les forces devraient être deux fois plus faibles. Mais encore faut-il que les propriétés de l'éther (ou de l'espace) demeurent inchangées. Or ce n'est guère concevable s'il prend de l'expansion. Une hypothèse plausible. Ainsi donc, il suffit de modifier certains paramètres pour que la Relativité de l'expansion ne soit plus "parfaite" et devienne mesurable. Il pourrait s'agir de la vitesse de la lumière, de la puissance des forces mécaniques ou encore de l'inertie de la matière. Il s'agit de faire en sorte que le redshift devienne apparent (puisque nous l'avons bel et bien constaté!) sans que la logique de l'ensemble ne soit détruite. La plupart des hypothèses conduisent pourtant à des contradictions ou à des anomalies inconcevables, mais on peut repérer certaines combinaisons qui ne détruisent pas forcément la logique de l'ensemble. Bref, si les astronomes avaient retenu une hypothèse plus vraisemblable à l'époque de Hubble, M. Perlmutter aurait pu la préciser encore davantage sans devoir invoquer l'existence "d'énergie noire". D'ailleurs, il suffit d'invoquer l'élasticité de l'éther pour expliquer son expansion, et même son expansion accélérée. Une telle force d'expansion ne peut s'expliquer que par les propriétés de l'éther et non par les lois de Newton, qui ne s'appliquent qu'à la matière. La force d'expansion de l'éther transcende la mécanique de la matière. Elle permet donc de justifier tout naturellement des vitesses bien supérieures à celle de la lumière sans devoir faire intervenir des quantités d'énergie absolument inconcevables. |
| 01 | 02 | 03 | 04 | 05 | 06 | 07 | 08 | 09 | 10 | 11 | Vous êtes ici. | 13 | 14 | 15 | 16 |
| 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 |
|
Gabriel La Frenière Bois-des-Filion en Québec. Dernière mise à jour le 31 mars 2011. Sur l'Internet depuis septembre 2002. Courrier électronique : veuillez consulter cet avis. La théorie de l'Absolu, © Luc Lafrenière, mai 2000. La matière est faite d'ondes, © Gabriel Lafrenière, juin 2002. |
ANTONIVS·MORO·BRVTVS·EST