LE PRINCIPE DE HUYGENS
L'angle d'inclinaison de la lame séparatrice de l'interféromètre de Michelson doit varier selon sa vitesse.
Cet angle correspond à la contraction proposée par Lorentz, ce qui démontre que cette explication était correcte
Le principe de Huygens permet de reproduire tous les phénomènes ondulatoires.
Ce principe n'a jamais été pris en défaut : il se vérifie toujours, mais à la condition d'en respecter les conditions.
![]()
![]() Page d'accueil :
La
matière est faite d'ondes.
Page d'accueil :
La
matière est faite d'ondes.
UN OUTIL INDISPENSABLE
|
Puisque la matière est faite d'ondes, le principe de Huygens deviendra désormais un outil très utilisé en physique. Toutefois le plus efficace sera incontestablement la méthode de modélisation d'un milieu élastique par ordinateur mise au point par Philippe Delmotte. À l'aide de son propre algorithme, M. Jocelyn Marcotte est déjà parvenu reproduire mon électron mobile, ce qui démontre que je n'avais pas tort ; et ce n'est qu'un début. Le principe de Huygens peut donc maintenant être vu comme un moyen de contre-vérifier de que ce médium virtuel révèle. C'est sans doute le principe de physique le plus mal compris. C'est d'autant plus regrettable qu'il permet à lui seul d'évaluer la plupart des phénomènes ondulatoires d'une manière aussi simple que spectaculaire. Un grand nombre des animations qui figurent dans ces pages font appel uniquement à lui. Voici comment Huygens a énoncé le principe qui porte son nom : |
|
« Nous pouvons considérer que tous les points atteints en même temps par l'onde sont les centres d'ondelettes qui se renforcent sur leur enveloppe commune : l'onde principale. L'énergie n'est appréciable que sur celle-ci. » |
Le principe de Huygens.
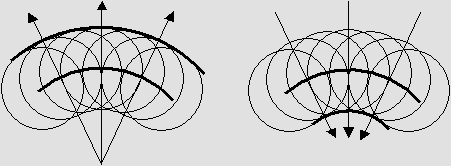
L'onde suivante se construit à partir des ondelettes créées sur le front de l'onde précédente.
|
Augustin Fresnel a quelque peu modifié le principe de Huygens pour qu'il corresponde à sa propre conception de la nature ondulatoire de la lumière : |
|
« Les vibrations d'une onde lumineuse dans chacun de ses points, peuvent être regardées comme la résultante des mouvements élémentaires qu'y enverraient au même instant, en agissant isolément, toutes les parties de cette onde considérée dans l'une quelconque de ses positions antérieures. » |
Le principe de Fresnel.
|
Cette version remaniée du principe de Huygens est en effet un peu plus précise. Personnellement, je pense qu'il est regrettable que Fresnel ne parle plus des célèbres ondelettes, puisqu'il apparaît aujourd'hui que ces ondelettes existent vraiment dans le cas de la lumière. Mais le résultat est le même : il est évident que, toutes les parties de l'onde agissant isolément, elles ne peuvent agir en différents points d'un espace à trois dimensions que sous la forme d'ondelettes. La vérité, c'est que le principe de Fresnel est faux dans le cas de la lumière. Les électrons émettent effectivement de telles ondelettes, qui sont donc bien réelles. Le problème, c'est qu'elles agissent à deux niveaux différents, d'une part sur la fréquence des électrons, qui est fixe et très élevée, et d'autre part sur la fréquence secondaire composite de la lumière qui en résulte. C'est pourquoi il convient de préciser la manière dont il faut appliquer le principe de Huygens. Le point important, c'est que les ondulations reproduites par les électrons sous l'action de la lumière incidente sont émises en opposition de phase. Il est donc impossible de justifier la réflexion de la lumière sur un miroir ou celle des ondes radio sur un réflecteur métallique plan à l'aide du principe de Huygens tel que ce dernier l'a formulé. On sait très bien depuis longtemps que cette réflexion s'effectue en opposition de phase. C'est typique d'une réflexion dite "dure". Seul, le son et les ondes similaires se comportent comme Huygens l'a prédit puisque leur réflexion sur un écran plat est plutôt "douce" ou "molle". Il faut alors préciser que la moitié des ondelettes est interceptée par l'écran et que l'énergie correspondante est redistribuée dans les mêmes ondelettes de manière à justifier à la fois l'ombre que l'écran produit et la loi de la conservation de l'énergie. Je suis donc plutôt choqué de voir que personne à ce jour, du moins en autant que j'ai pu le vérifier, ne signale ce fait capital. Les ondes des électrons et de la matière se comportent en effet comme Huygens l'a montré. Mais la lumière et les ondes radio, qui sont faites des mêmes ondes, se caractérisent par des ondulations qui s'effectuent sur une fréquence secondaire beaucoup plus basse. Elles traversent systématiquement toute matière sans subir la moindre modification, ce qui évite d'avoir à signaler qu'elles sont interceptées. Dans les faits, ce sont les électrons qui sont atteints la lumière incidente qui émettent de nouvelles ondelettes de lumière, dont les ondulations vibrent en opposition de phase au moment de leur émission. Cette nouvelle lumière se compose avec la lumière incidente, et le résultat explique enfin tous les phénomènes de couleur, de polarisation, d'ombre, d'amortissement, de réflexion, de réfraction, de dispersion et même de transmission à travers une substance transparente. Les ondelettes fictives sont en phase. Dans un premier temps, il faut comprendre que la propagation des ondes progressives simples, celles du son par exemple, se fait strictement selon les prévisions de Huygens. On invoque alors la présence fictive d'ondelettes, et alors ces ondelettes sont en phase avec l'onde principale. C'est donc le cas s'il faut étudier le mode de propagation normal d'un son à travers un gaz, un liquide ou un solide, et même sa réflexion sur un écran ou sa réfraction à travers un médium d'indice différent. Et c'est encore le cas en ce qui concerne les ondes stationnaires de l'électron et de la matière, qui prélèvent de l'énergie aux ondes qui circulent dans l'éther. À l'intérieur d'un électron ou d'un champ de force, il se produit une émission d'ondes progressives additionnelles. Il faut donc considérer que ces ondes sont le résultat de l'addition d'ondelettes fictives qui ont pris naissance sur les ventres successifs, en respectant la période de ces ventres. Les ondulations de la lumière sont reproduites en opposition de phase. D'un autre côté, la lumière est faite d'ondes composites dont la fréquence fixe et très élevée correspond à celle des électrons. Il s'agit d'ondes composites pulsées sur une fréquence secondaire, ce qui explique qu'on puisse obtenir aussi bien des rayons gamma que des ondes radio kilométriques à partir des mêmes ondelettes à fréquence unique émises par les électrons. On est donc en présence d'ondelettes véritables. C'est donc le cas en particulier lorsque la lumière atteint un miroir, plus exactement les électrons présents sur sa surface métallique et sur une épaisseur inférieure à sa longueur d'onde. On sait bien que la lumière exerce une pression de radiation, et il se trouve qu'il existe deux sortes d'électrons : ils ont un spin. J'ai montré qu'ils vibrent en opposition de phase, et l'action de la lumière a pour effet de les aligner différemment sur le front de ses ondes. Ils tendent à se répartir selon leur spin, de sorte que leur structure tend à devenir équiphasée. Or on sait que le fait de répartir de nombreux émetteurs sur un plan équiphasé a pour effet de produire un rayonnement sur un même axe, de part et d'autre de ce plan. On aura vu à la page sur la lumière que son rayonnement ondule transversalement de manière à permettre une polarisation. Les électrons atteints par la lumière ont donc tendance à suivre les mêmes ondulations et à les reproduire, mais celles-ci s'effectuent en opposition de phase (sur l'axe d'origine) comparativement avec celles de la lumière incidente. Cette opposition de phase s'explique par le fait que le noyau de l'électron présente une inversion de phase. Ainsi, toutes les fois que la lumière atteint la matière, celle-ci réagit en émettant de la nouvelle lumière, dont la période est en opposition de phase. On verra plus loin que ce détail fait toute la différence : il explique pourquoi la lumière réfléchie (mais en réalité créée de toutes pièces) par un miroir est en opposition de phase. Mais, et c'est là le point important, il indique que la lumière traverse les objets sans rencontrer la moindre opposition. Malgré les apparences, elle n'est pas réfléchie. Si elle devient invisible derrière le miroir de manière à produire une ombre, c'est parce que les nouvelles ondulations sont en opposition de phase et qu'elles provoquent des interférences destructives. La réflexion. En plus du mode de propagation normal des ondes progressives de la lumière, qu'elles soient planes, sphériques et même stationnaires, Huygens a pu expliquer tout particulièrement la réflexion et la réfraction. Mais il n'avait pas conscience que ce n'était vrai que dans le cas du son. L'animation suivante montre comment le son est réfléchi sur un écran plat : |

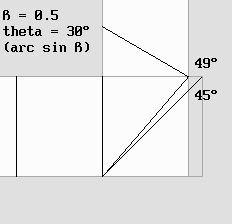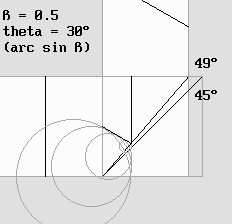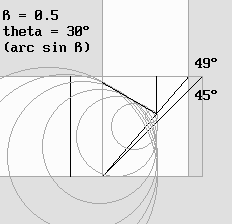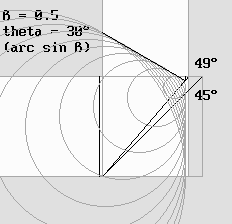
La réflexion d'une onde sonore sur un écran incliné de 45°.
Des ondelettes fictives produisent un front d'ondes réfléchi dont l'angle varie selon l'angle d'inclinaison de l'écran.
Noter que les ondelettes traversent l'écran, ce qui donne à penser que l'onde incidente devrait faire de même.
Il est donc nécessaire de postuler que les ondelettes sont interceptées par l'écran, ce qui va de soi dans le cas du son.
On a vu que la lumière, au contraire, n'est jamais interceptée par la matière.
C'est pourquoi ce deuxième front, étant en opposition de phase, provoque la formation d'une ombre par interférences destructives.
|
Huygens parle des points atteints en même temps par l'onde, mais on remarque ici que les ondelettes naissent à des instants différents sans problème. Il faudra donc biffer ces mots de la formulation révisée du principe de Huygens, mais cela nous obligera à préciser qu'il faut tenir compte de la différence de marche. Le principe de Fresnel de son côté ne le laisse entendre qu'à mots couverts. En effet, chacune de ces ondelettes est une onde sinusoïdale à part entière : elle présente une rotation de phase selon la distance entre son point de départ et l'endroit qu'elle atteint, plus exactement selon le temps qu'elle met à parcourir cette distance. La réfraction du son. L'animation ci-dessous avait été faite pour illustrer la réfraction de la lumière lorsqu'elle pénètre dans le verre. Mais on a vu qu'une telle réfraction s'explique autrement dans le cas de la lumière. Elle montre donc plutôt le comportement du son, mais il faut se rappeler que la vitesse du son est plus rapide dans le verre que dans l'air. La partie supérieure montrée en blanc devrait donc représenter le verre et la partie inférieure, l'air. |
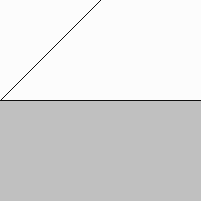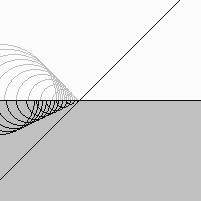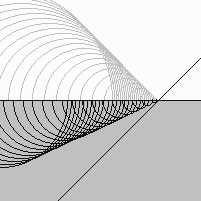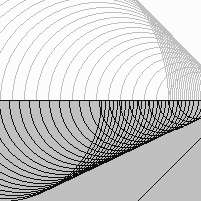
La réfraction du son s'il passe du verre à l'air.
Il se produit une faible réflexion selon le "facteur d'inclinaison" de Kirchhoff.
C'est que les ondelettes se détruisent davantage si elles sont créées sur une grande profondeur.
Quand le son pénètre dans l'air, l'angle du nouveau front d'ondes est modifié car la vitesse des ondelettes est réduite.
|
Les ondelettes négatives. Selon Huygens, l'onde principale se régénère continuellement comme si elle émettait constamment de nouvelles ondelettes. Malheureusement, la plupart des représentations qu'on a faites de ce phénomène ne montrent que des ondelettes qui prennent naissance sur un seul plan, aux endroits où la période de l'onde principale est à zéro. Cela ne montre pas très bien ce qui se passe à l'arrière de l'onde. Certains en ont déduit à tort que le principe de Huygens n'indique pas pourquoi l'onde ne se propage pas simultanément vers l'arrière. Or on peut multiplier les endroits où les ondelettes prennent naissance, ce qui permet de démontrer que l'onde principale n'a qu'un seul sens. De plus, puisque les ondelettes sont des ondes à part entière, elles présentent une amplitude négative à chaque demi-période. Il est souvent utile d'en tenir compte pour préciser leur évolution. Le diagramme ci-dessous montre l'onde principale en blanc là où l'amplitude est au maximum, et en noir là où elle atteint le minimum du côté négatif : |

Les ondes progressives ne se propagent que dans un sens.
Les ondelettes positives représentées en blanc et négatives, en noir, restent bien séparées vers l'avant.
Mais elles provoquent des interférences destructives vers l'arrière : leur effet est annulé.
LES ONDELETTES ÉMISES PAR LES ÉLECTRONS SONT EN OPPOSITION DE PHASE
|
C'est un fait bien établi : la lumière réfléchie par un miroir est en opposition de phase. Il faut convenir que même le principe de Huygens tel que reformulé par Augustin Fresnel ne rend pas compte de ce fait. Il vaut mieux reformuler plutôt le principe de Huygens, de manière à préciser que la lumière incidente force les électrons à émettre de la nouvelle lumière. Les ondulations transversales de celle-ci sont en opposition de phase comparativement à celles de l'onde incidente. D'une part, cela permet de montrer que la lumière réfléchie par un miroir est en opposition de phase. Mais d'autre part, il devient clair que même les ondelettes qui traversent le miroir sont également en opposition de phase. De plus, nous avons vu plus haut que la lumière incidente traverse le miroir sans rencontrer la moindre opposition. Dans ces conditions, les deux se superposent et cela produit des interférences destructives, c'est à dire une ombre derrière le miroir : |

Le principe de Huygens reformulé montre que le miroir atteint par la lumière incidente émet d'autre lumière en opposition de phase.
Cela permet du même coup de démontrer que le miroir produit une ombre derrière lui.
Croyez-le ou non, la lumière d'origine traverse le miroir sans rencontrer la moindre opposition.
Mais son effet est annulé à cause de la présence de la nouvelle lumière, qui est en opposition de phase.
|
Nous savons depuis longtemps que la matière est faite de vide à toutes fins pratiques, tellement la taille des particules qu'elle contient est faible. En réalité ses ondes stationnaires occupent un espace considérable, mais elles sont tout aussi incapables d'intercepter d'autres ondes. D'autre part, il est trop facile de justifier la lumière par des photons et des champs électromagnétiques sans préciser davantage de quoi il s'agit. Admettons-le, personne n'a jamais vraiment expliqué la lumière, sauf Descartes et Huygens. Ces derniers ont vu juste : il s'agit bel et bien d'ondes, et la matière qui est elle aussi faite d'ondes est incapable de les intercepter. C'est pourquoi la présente explication par des ondelettes de Huygens véritables devient la seule qui soit acceptable. On sait que Gustav R. Kirchhoff a étudié le principe de Huygens. J'ose affirmer que depuis que les ordinateurs existent, tous ses calculs sont dépassés : il suffit d'écrire un programme qui additionne l'amplitude d'un grand nombre d'ondelettes et qui affiche les résultats en différents tons de gris pour obtenir à coup sûr des résultats identiques à ce que l'expérience révèle. On verra plus loin que cette méthode est élémentaire. Les ondes stationnaires. L'animation suivante montre comment les ondelettes de Huygens fictives évoluent à travers les ondes stationnaires : |

Les ondelettes de Huygens expliquent aussi les ondes stationnaires.
Mais cette représentation n'est pas très convaincante.
Heureusement, l'ordinateur peut faire beaucoup mieux.
|
Cette animation apparaît quelque peu obscure même si les ondelettes produisent des résultats corrects. Le problème, c'est que ce procédé est très imparfait : il ne montre que les phases positives et négatives des ondelettes sous la forme de cercles blancs ou noirs. Il ne montre donc pas les variations d'amplitude correctes de l'onde résultante. Or l'ordinateur peut calculer avec une précision remarquable le total des ondelettes selon leur période et leur amplitude, ce qui produit des résultats stupéfiants. C'est ce que nous allons voir maintenant. |
COMMENT INTÉGRER LES ONDELETTES SUR ORDINATEUR.
|
Généralement, on ne fait appel au principe de Huygens que pour expliquer quelques phénomènes ondulatoires comme la réflexion et la réfraction. Pourtant, pour peu qu'on y réfléchisse, on se rend vite compte que l'idée de faire intervenir ces fameuses ondelettes est géniale. Je le répète : on peut de cette manière évaluer la plupart des phénomènes ondulatoires. Les échantillons. Selon Huygens, tous les points atteints pas l'onde sont les centres d'ondelettes. En principe, le nombre de ces points est infini. Mais en pratique, comme on l'a vu plus haut, un nombre relativement grand d'ondelettes suffit : ce seront des échantillons. C'est la loi des grands nombres, une règle de base des statistiques, qui fait en sorte qu'au delà d'un certain point, on atteint la quasi-certitude. L'expérience montre que quelques centaines de points seulement répartis uniformément sur une calotte sphérique circulaire produisent le diagramme classique de la tache d'Airy sans problème. L'ordinateur étant très rapide, il est facile de répéter le processus avec de plus en plus d'échantillons. Il suffit de repérer le nombre de points au-delà duquel il ne se produit plus aucun changement pour disposer par la suite d'un programme très efficace qu'on pourra adapter à toutes sortes de situations. Il s'agit à toutes fins pratiques d'un calcul intégral, mais sans les complications usuelles. L'ordinateur effectue la sommation de toutes les ondelettes pour un point donné de l'espace à la vitesse de l'éclair. Il existe d'ailleurs des moyens d'accélérer encore les temps de calcul, par exemple en évaluant des courbes équiphasées plutôt que des points, ou en utilisant un langage de programmation évolué, sans oublier les ressources graphiques fantastiques et la mémoire stupéfiante des ordinateurs actuels. Le calcul des ondelettes. Afin que vous puissiez vérifier par vous-même que les conclusions de cette étude sont tout à fait raisonnables, je vous propose d'examiner la structure des programmes que j'utilise pour évaluer ces ondelettes. Soyez sans crainte : ces programmes sont élémentaires. N'importe quel étudiant capable d'écrire un programme d'ordinateur peut les comprendre. Il s'agit des programmes qui ont été utilisés pour produire les diagrammes montrés plus bas. Je vous suggère cependant de procéder par étapes pour mieux assimiler la procédure. Vous pouvez cliquer sur chacun des diagrammes pour n'obtenir que le programme concerné. Ces programmes sont rédigés en Quick Basic (le programme QB.EXE est disponible avec les versions anciennes de Windows) et ils ne fonctionnent qu'avec les ordinateurs de type IBM : ils sont donc incompatibles avec Macintosh. Le fichier ZIP contient le code source, la version exécutable et un exemplaire des images que le programme produit. Je présume que la plupart de ceux qui savent programmer un ordinateur les comprendront sans peine. Ils devraient idéalement les traduire en C++. De toutes façons, on ne maîtrise bien que les programmes qu'on a soi-même écrits. La première étape consiste à ne calculer qu'une seule ondelette : |
Une ondelette de Huygens.
Selon Huygens, les ondelettes naissent sur le front de l'onde principale et elles sont en phase avec elle.
Il faut aussi tenir compte de l'affaiblissement : l'amplitude est inversement proportionnelle à la distance.
L'énergie valant le carré de l'amplitude selon Fresnel, elle faiblit donc selon le carré de la distance.
|
Cliquez sur l'image pour télécharger le programme qui a été utilisé pour réaliser cette animation. |
|
La période d'une onde pour un point donné de l'espace dépend de la différence de marche comparativement à un multiple entier de la longueur d'onde. Il s'agit de convertir la distance en longueurs d'onde. En optique, l'expérience montre qu'il faut tout évaluer en millimètres parce que les distances se situent généralement entre un millimètre et un mètre, alors que la longueur d'onde de la lumière verte, que l'œil voit le mieux et qui est universellement acceptée comme standard, vaut 0,00055 mm. Le millimètre constitue donc une moyenne très pratique.Toutefois, dans un premier temps, il sera préférable d'évaluer les distances en pixels. C'est qu'il s'agira d'afficher les résultats sur l'écran de l'ordinateur, les commandes graphiques étant conçues à cette fin. 1 - Calculer la différence de marche. Il est évident que si le pixel à évaluer se situe à une demi-longueur d'onde du point d'origine d'une ondelette, sa période sera en retard d'une demi-période sur celle de ce point d'origine. Elle dépend en réalité du délai écoulé. Mais il en sera de même pour n'importe quel multiple entier de la longueur d'onde plus une demi-onde supplémentaire. En conséquence, il s'agit dans un premier temps de calculer la distance entre le point à évaluer et le centre de l'ondelette, puis de convertir cette distance en longueurs d'ondes. Supposons que les coordonnées du point d'origine de l'ondelette sont : x = 200 ; y = 300. On suppose aussi que la longueur d'onde est de 40 pixels : lambda = 40 Le point à évaluer se situe en x ' = 300 ; y ' = 150. Distance sur l'axe x : 300 – 200 = 100 Distance sur l'axe y : 150 – 300 = –150 Distance réelle selon Pythagore : ( (100 * 100) + (–150 * –150) ) (1 / 2) = 180 pixels. Distance exprimée en longueurs d'onde : 180 / 40 = 4,5 variableVirguleFlottante = 4,5 variableNombreEntier = 4 differenceDeMarche = variableVirguleFlottante – variableNombreEntier = 0,5 Pour éviter « l'effet papillon », il vaut mieux utiliser systématiquement les variables de type virgule flottante à double précision. En effet, des milliers d'imprécisions négligeables qui s'additionnent peuvent éventuellement (mais rarement) conduire à une seule imprécision catastrophique. 2 - Calculer la période. La différence de marche étant en longueurs d'onde, on peut ensuite établir la période de l'ondelette en la comparant à : 2 * pi. phase = differenceDeMarche * 2 * pi on a donc ici : phase = 0,5 * 2 * pi = 3,14159 Je présume que vous savez que le chiffre pi correspond à : pi = 4 * arc tan (1). Les angles étant exprimés en radians, 360° correspond à 2 pi, et donc 180° = 3,14159 radians correspond à l'opposition de phase. 3 - Afficher l'onde. Le sinus de la période correspond à la phase et son cosinus, à la quadrature. Personnellement, je préfère afficher l'onde selon le cosinus de la période. C'est que je montre très souvent des ondes stationnaires, qui ne sont pas visibles à la période 0 si c'est le sinus qu'on utilise. Il s'agit de convertir la période en différents niveaux de gris : couleur = cosinus (phase) + 1 couleur = COS (3,14159) + 1 couleur = – 1 + 1 couleur = 0 (noir) On obtient des chiffres variant de 0 à 2 qu'il faut surmultiplier pour couvrir les tons de gris disponibles. Dans l'ancien mode graphique VGA (640 x 480 pixels), il n'existe que 16 couleurs RVB qu'on peut heureusement convertir en 16 tons de gris comme le montrent mes programmes. C'est M. Philippe Delmotte qui m'a appris ça (ce n'était pas dans les 710 pages de mon grand livre sur le Quick Basic). On peut même les inverser de manière à afficher le texte en noir sur blanc. Parce que ces 16 couleurs peuvent être indexées dans le format GIF, on obtient des images beaucoup plus économes en octets que dans le format JPEG. C'était le cas de la plupart de mes images anciennes, et j'utilisais une astuce qui permet de diffuser les valeurs sur 4 pixels sans perte de résolution de manière à obtenir finalement 64 tons de gris. Bien sûr, tout ça est de l'histoire ancienne. Les ordinateurs d'aujourd'hui sont bien plus rapides qu'en 1995 et le langage de programmation FreeBasic est infiniment plus efficace que le Quick Basic. Mais voilà, c'était ainsi qu'on procédait en 1995 et j'en suis très fier étant donné les résultats que j'ai obtenus en optique à cette époque, alors que je travaillais sur mon ouvrage "Optique des miroirs". J'ai ainsi pu analyser un grand nombre de configurations d'appareils optiques à miroir, dont certains munis de lentilles ou de correcteurs en verre optique. Plusieurs de ces appareils sont des inventions originales. 4 - Afficher l'amplitude s'il y a deux ondelettes ou plus. L'ordinateur a ceci de fantastique qu'il peut traiter mille ondelettes à peu près aussi rapidement que s'il y en a deux seulement. Il suffit d'insérer les équations montrées plus haut dans une boucle pour en traiter autant que c'est nécessaire. Le calcul se résume à une simple addition : amplitudeSinus = amplitudeSinus + SIN (phase) amplitudeCosinus = amplitudeCosinus + COS (phase) Le sinus et le cosinus étant associés aux côtés d'un triangle rectangle, ils permettent d'évaluer l'hypoténuse selon le théorème de Pythagore. Mais ils permettent de la même manière d'évaluer l'énergie et l'amplitude finales en un point donné de l'espace : Energie = ( (amplitudeSinus * amplitudeSinus) + (amplitudeCosinus * amplitudeCosinus) ) Amplitude = Sqr(Energie) On conviendra que la sommation des ondelettes est élémentaire. C'est ainsi qu'on peut finalement montrer comment deux ou plusieurs ondelettes se composent : |
La composition de deux ondelettes.
Il suffit d'additionner l'amplitude des deux ondes : rien de plus.
Si elles sont positives et négatives, leur total est réduit par interférences destructives.
On retrouve les ellipses concentriques et les hyperboles habituelles.
Ce diagramme ne montre pas les ondes, mais seulement leur énergie
Les zones où l'énergie est nulle sont affichées en noir.
On peut même superposer les deux images, ce qui produit un diagramme composite très révélateur.
|
La tache d'Airy. En procédant exactement de la même manière, on peut répartir uniformément un grand nombre de sources d'ondelettes sur la surface d'un cercle. Il existe plusieurs méthodes, mais voici celle que j'affectionne le plus. Le fait que les points où se situe leur origine soient répartis selon des couronnes concentriques permet d'éviter de refaire une partie du calcul à chaque point, et donc d'accélérer ce calcul : |

Les centres des ondelettes sont répartis uniformément sur la surface d'un cercle.
Comme l'indique Huygens, chaque point est atteint simultanément par l'onde principale, si elle est plane.
Toutes ces ondelettes ajoutent ou retranchent leur amplitude selon qu'elles sont en phase ou en opposition.
Attention : il est essentiel de calculer la différence de marche dans un espace en trois dimensions.
L'autre moitié de cet espace étant symétrique, il suffit en pratique de n'en évaluer que la moitié.
Les ondelettes qui en résultent produisent le diagramme suivant :
|
|
Le diagramme d'amplitude du faisceau d'un laser ou d'un sténopé (la caméra à trou).
C'est l'exemple typique de ce qu'il est convenu d'appeler la diffraction de Fresnel.
On remarque que la tache d'Airy définitive (la diffraction de Fraunhofer) ne commence à se former qu'à l'extrême droite.
C'est ce qui explique que le sténopé ne peut produire une image acceptable qu'au delà d'une certaine distance.
|
Le diagramme montré ci-dessus est plus exactement celui du faisceau lumineux qu'on obtient en dirigeant le faisceau d'un laser très éloigné à travers une petite ouverture circulaire d'environ 5 mm percée dans un écran opaque. C'est donc aussi le faisceau lumineux qu'on obtient en tentant de photographier ce laser éloigné (qui devient une étoile artificielle) à l'aide d'un sténopé. Si des points équiphasés sont répartis sur la surface d'une calotte sphérique (et non pas d'un disque plat), on obtient plutôt une tache d'Airy parfaite au centre de courbure de la calotte : c'est ainsi que l'image se forme au foyer d'une lentille ou d'un télescope à miroir : |
|
|
Cette vue longitudinale de la tache d'Airy à ƒ / 2 comprend l'axe optique.
On constate que le tache d'Airy est en fait la section d'un ellipsoïde allongé, ce qu'on mentionne rarement.
D est le diamètre de l'objectif, F est la focale, lambda est la longueur d'onde, et R est le rayon de la tache d'Airy :
R = 1,22 * lambda * F / D
Exemple : lambda = 0,00055 mm ; F = 200 mm ; D = 100 mm ; ouverture relative « ƒ » = F / D.
On a donc une ouverture relative de ƒ / 2 et le rayon de la tache d'Airy vaut alors : R = 0,00134 mm.
|
|
À droite, la tache d'Airy entourée d'anneaux tel qu'elle apparaît au foyer d'un télescope.
À gauche, il est représenté en relief de manière à en souligner l'amplitude.
|
Je vous invite donc à examiner le code source des programmes qui me permettent d'évaluer les ondes. Je tiens à rappeler qu'il s'agit d'une application du principe de Huygens. L'ordinateur fait désormais partie de nos vies, et les physiciens qui n'auront pas appris la programmation traîneront loin derrière. Beaucoup de correspondants me reprochent de ne pas présenter suffisamment d'équations. Soyons clair : c'est inutile, du moins à ce stade-ci. Les programmes que je propose font beaucoup mieux. Même si vous détenez un doctorat en physique, vous seriez mal venu de critiquer ce site si vous ne possédez qu'une connaissance limitée des ondes et si n'avez pas vérifié mes résultats. Ces résultats se vérifient aussi par le calcul différentiel si vous y tenez, mais c'est votre choix ; pas le mien. Par ailleurs, la matière est une affaire de mécanique ; les mathématiques ne sont qu'un outil. Ce n'est que lorsqu'on sait comment elle fonctionne qu'on peut ensuite, mais seulement ensuite, en calculer raisonnablement les manifestations. Si j'ai placé cette page à la toute fin de ce site, c'est pour que vous le quittiez avec un nouvel outil qui s'avère incroyablement efficace. Je souhaite que les gens qui savent encore se servir de leur intelligence s'affranchissent enfin de cette physique aberrante dominée par les mathématiques. Désormais, toute la physique fera appel aux ondes. Si vous apprenez à écrire des programmes fondés sur le principe de Huygens, vous y aurez gagné car votre connaissance des ondes n'en sera que meilleure. Et alors, au lieu de rejeter en bloc tout ce que j'affirme en vous appuyant sur des prémisses erronées, vous pourrez le vérifier. Si vous avez un minimum d'intelligence, vous devriez convenir par exemple que la lumière pourrait tout aussi bien traverser les objets comme je l'affirme. C'est ce que le principe de Huygens indique, s'il est appliqué correctement en considérant les électrons et leur mécanique. Bien sûr, vous devriez aussi savoir utiliser les algorithmes Delmotte et Marcotte, qui permettent de créer un médium virtuel informatique dont les possibilités sont infinies. Peut-être même pourrez-vous découvrir une toute nouvelle approche à laquelle je n'avais pas songé. |
| 01 | 02 | 03 | 04 | 05 | 06 | 07 | 08 | 09 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | Vous êtes ici. | 33 |
|
Gabriel LaFrenière, Bois-des-Filion en Québec. Sur l'Internet depuis septembre 2002. Dernière mise à jour le 19 septembre 2009. Courrier électronique : veuillez consulter cet avis. La théorie de l'Absolu, © Luc Lafrenière, mai 2000. La matière est faite d'ondes, © Gabriel Lafrenière, juin 2002. |