LES ONDES STATIONNAIRES D'IVANOV
 |
Les ondes stationnaires continuent de présenter des ventres et des nœuds si la longueur des ondes progressives arrivant en sens opposé diffère.
M. Yuri Ivanov a montré en 1990 que ce système se déplace à une vitesse qui dépend du rapport de ces longueurs d'onde.
Il en a conclu que ces « ondes stationnaires animées » transportent l'énergie qu'elles contiennent à cette même vitesse.
Il a aussi montré que ces ventres et ces nœuds se contractent d'autant plus que leur vitesse est élevée.
Et enfin, l'ensemble présente la fameuse « onde de phase » dont parle Louis de Broglie.
![]()
![]() Page d'accueil :
La
matière est faite d'ondes.
Page d'accueil :
La
matière est faite d'ondes.
|
Vous trouverez ci-dessous une expérience très intéressante. Elle montre toutes les propriétés des "ondes d'Ivanov" en un seul jet. Puisque la matière est faite d'ondes stationnaires, une telle expérience s'imposait. J'ai pris soin de limiter les formules nécessaires au minimum et de les simplifier au maximum pour faire en sorte que cette expérience ne laisse place à aucune discussion possible. Ici, vous avez des faits. Rien que des faits. Je vous rappelle que vous pouvez télécharger les programmes que j'ai écrits dans le but de produire ces séquences en les repérant dans l'un des répertoires ci-dessous, que j'ai rendus publics. VidéosIl s'agit véritablement d'une expérience puisque j'ai eu recours au médium virtuel Delmotte-Marcotte pour obtenir l'effet Doppler. Tout y est: l'onde de phase, la contraction prévue par Lorentz, le déplacement de la structure ondulatoire à la même vitesse que celle des émetteurs et enfin, le transport de l'énergie à cette même vitesse, puisqu'elle ne peut pas franchir chacun des nœuds. Faut-il rappeler que la matière présente manifestement des propriétés ondulatoires et que Louis de Broglie a parlé d'ondes stationnaires? Il a aussi parlé d'une onde de phase et d'une vitesse de groupe. Il a même souligné que la vitesse de la lumière correspond à la moyenne géométrique entre cette vitesse et celle de l'onde de phase. Pour ma part, je m'emploie depuis longtemps à montrer que les ondes stationnaires présentent de leur côté les mêmes propriétés que la matière. Nous avons donc ici à la fois le début et la fin d'une démarche, de sorte que ce qu'il reste à trouver entre les deux est hautement prévisible. Il s'agit d'une avenue qu'il devient urgent d'explorer soigneusement pour sortir enfin la physique de l'ornière dans laquelle elle s'est enlisée depuis un siècle... L'origine du facteur de contraction de Lorentz. On sait que la fameuse "aberration" dont parle abondamment Henri Poincaré, qui fut le fer de lance de la théorie de Lorentz, est une découverte de Michelson bien antérieure à 1887. Elle a permis à ce dernier de mettre au point son célèbre interféromètre, qui on le sait a abouti à un résultat nul tout à fait surprenant. On la retrouve au dénominateur des équations présentées par Lorentz en 1904, que Poincaré a appelées "transformations de Lorentz" bien qu'elles aient été mises au point en réalité par Woldemar Voigt dès 1887. Il s'agit de ce que j'appelle ici le facteur de contraction de Lorentz, identifié par la lettre "g". C'est l'inverse du facteur gamma mis en avant par Poincaré en 1901, donc bien avant Einstein, pour démontrer son "Postulat de Relativité". Ci-dessous, M. Christian Marchal a transposé les équations de Poincaré en notation d'aujourd'hui. Poincaré ayant préféré placer le facteur de contraction au numérateur, il est devenu l'inverse sous le nom de "facteur gamma" (gamma = 1 / g):
De plus, Lorentz a trouvé que la constante de Voigt identifiée ci-dessus par la lettre l pouvait être éliminée puisqu'elle devait être égale à 1. Or Lorentz ayant fait l'erreur de confondre t et t', il fallait inverser ces équations comme on le montre ci-dessous pour qu'elles produisent des résultats corrects. Alors le facteur de contraction de Lorentz s'en trouve déplacé au numérateur sans qu'il soit nécessaire de le convertir en facteur gamma. Ce dernier doit donc être abandonné. Sans aucun doute, il vaut beaucoup mieux parler d'un facteur de contraction identifié ici par la lettre "g" puisque Lorentz parlait bien d'une contraction de l'interféromètre de Michelson. On obtient finalement ceci:
Je suis très fier d'avoir réussi à identifier la cause profonde, l'origine véritable de cette "aberration". À la seule condition de disposer de deux longueurs d'onde distinctes, j'ai en effet trouvé que le facteur de Lorentz g peut être obtenu en trouvant le rapport de leur moyenne géométrique sur leur moyenne arithmétique. On a tout simplement: g = [moyenne géométrique] / [moyenne arithmétique]. Avant même de parler de Relativité, ce facteur est donc beaucoup plus simplement lié au comportement des ondes stationnaires. Il est bien évident que tout émetteur en mouvement produit un effet Doppler aboutissant à deux longueurs d'ondes distinctes, l'une vers l'avant (blueshift) et l'autre vers l'arrière (redshift). Et puisqu'il est bien connu que le rapport de ces deux moyennes conduit tout droit au théorème de Pythagore, il convient d'examiner ceci de ce point de vue.
Ce tableau est en soi un véritable théorème voulant que la moyenne arithmétique et la moyenne géométrique des deux longueurs d'onde des ondes d'Ivanov équivalent à la vitesse de la lumière comparée au facteur de contraction g de Lorentz. De plus, le troisième côté du triangle correspond à la vitesse des ondes d'Ivanov, qu'on appellera ici la vitesse normalisée alpha. Ce tableau montre également que les transformations de Lorentz reflètent sans contredit le comportement des ondes stationnaires (transformations Alpha), même si j'ai dû inverser et même corriger les équations de Lorentz. Il est clair que Lorentz n'a pas su bien identifier ni définir les variables x et t car les mêmes équations s'appliquent aussi à l'électron (transformations Bêta) et à la matière (transformations Gamma). C'est tout à fait remarquable: les équations demeurent les mêmes. Il est toutefois essentiel de redéfinir ces variables pour qu'elles conviennent à chacun de ces trois phénomènes. Ainsi donc, à partir de seulement deux données fondamentales, soit la longueur des ondes qui circulent théoriquement en sens opposé, on peut prévoir la valeur de cette fameuse "aberration" dont parlait Poincaré. On peut obtenir ensuite non seulement la vitesse de déplacement "alpha" des ventres et des nœuds des ondes d'Ivanov, mais aussi la valeur de leur contraction et la vitesse de l'onde de phase. L'effet Doppler relativiste. Ce que la courte séquence vidéo suggérée plus haut montre clairement, c'est qu'il existe une différence fondamentale entre l'effet Doppler acoustique normal et l'effet Doppler dit "relativiste" de la lumière (et aussi de l'électron et donc de la matière). Dans le cas de l'effet Doppler acoustique, la contraction des ondes stationnaires vaut le "carré de l'aberration" dont parlaient d'abord Lorentz et Poincaré entre 1895 et 1904, donc le carré du facteur g. Mais on sait que Lorentz a découvert finalement et publié en 1904 qu'en plus de la contraction que devait subir l'interféromètre de Michelson selon le facteur g simple et non plus son carré, il devait se produire une ralentissement de la fréquence de la lumière, toujours selon ce même facteur g. Ce ralentissement, qu'on a appelé plus tard le "ralentissement du temps", s'applique également à la fréquence de l'électron et au comportement mécanique de la matière en mouvement, qui fait en sorte par exemple que les horloges fonctionnent plus lentement et indiquent donc des heures plus lentes. La vidéo montre bien que dans ce cas, les ondes stationnaires se contractent seulement selon le facteur g et non pas son carré. Lorentz a vu beaucoup plus loin que Poincaré et Einstein, qui n'ont jamais voulu admettre cette hypothèse par trop commode et donc suspecte (une "étrange propriété", un "coup de pouce" donné par la nature, comme l'a écrit Poincaré) d'une contraction de l'interféromètre de Michelson. Pourtant, il devient clair que Lorentz avait tout à fait raison. Ce faisant, il n'a pas seulement expliqué la Relativité, il a aussi posé les bases de la "mécanique nouvelle" mise en avant par Poincaré. On l'ignorait à l'époque, mais depuis les travaux de Louis de Broglie, on peut parler désormais de la mécanique ondulatoire. D'ailleurs, c'est Lorentz lui-même qui en a déduit que l'énergie et donc la masse de la matière devait augmenter avec sa vitesse, encore une fois en fonction du facteur g. Or il est bien connu que l'énergie des ondes est proportionnelle à leur fréquence et donc inversement proportionnelle à leur longueur. S'il se produit une contraction de la longueur d'onde, cela se traduit forcément par un gain en énergie qui justifie l'énergie cinétique. J'ai consacré toute une page à ce phénomène en faisant intervenir la masse active et la masse réactive qui résultent de l'effet Doppler relativiste. Un hommage à M. Yuri Ivanov. C'est à M. Yuri Ivanov que revient l'honneur d'avoir finalement expliqué cette contraction de l'interféromètre de Michelson en faisant le lien avec ses "ondes stationnaires animées", que j'appellerai du nom d'Ivanov. Bien qu'il ait fait l'erreur de rejeter le ralentissement de la fréquence pour aboutir à une contraction trop sévère, il a tout de même montré que les liaisons atomiques devaient se faire en fonction d'une certaine longueur d'onde. Il a très bien montré que si cette longueur d'onde se contracte, la matière elle-même doit se contracter. Il aussi montré que la vitesse de la matière correspond à la vitesse de ces ondes qui ne sont vraiment pas "stationnaires". Il a aussi montré que celles-ci transportent leur énergie avec elles, ce qui permet d'en conclure que la matière peut de la même manière transporter l'énergie qu'elle contient. Pour couronner le tout, il montre aussi sur son site que les ondes stationnaires s'influencent mutuellement. Il montre que si deux personnes occupent la même embarcation et lancent des pierres en sens opposé à tour de rôle, on obtient une représentation très réaliste du mécanisme qui permet à la matière de modifier son inertie naturelle pour accélérer ou ralentir. Lancer une pierre, c'est modifier son énergie, et cela ne peut se faire qu'en comprimant ou en dilatant ses ondes. Or en vertu de la loi de la conservation de l'énergie, il est nécessaire d'emprunter ou de céder de l'énergie à d'autre matière pour que cela puisse se produire. La matière et les ondes stationnaires présentent les mêmes propriétés. Voilà bien ce qu'il fallait réaliser : la matière et les ondes stationnaires se comportent de la même manière. C'est plus qu'il n'en faut pour affirmer que c'est parce qu'elle est faite d'ondes stationnaires que la matière se comporte ainsi. Selon sa vitesse, elle se contracte et elle accroît ainsi l'énergie qu'elle transporte avec elle. Cette énergie qu'elle accumule, c'est de l'énergie cinétique. J'ai d'ailleurs réussi à récupérer la formule newtonienne de l'énergie cinétique pour démontrer qu'il vaut beaucoup mieux repartir de là où Newton s'était rendu plutôt que de tout détruire comme on l'a fait vers 1900:
... ce qui est l'équivalent de : E = (gamma – 1) m c 2, et bien sûr mieux que : E = m v 2 / 2
C'est donc grâce à une partie de sa masse, accumulée sous forme d'énergie cinétique, que la matière peut agir et réagir avec d'autres matière à cause des ondes qu'elle émet et qu'elle reçoit, le tout selon les lois de Newton. Les champs de force. Et puisque les électrons qui composent la matière reçoivent et émettent des ondes simultanément, il en résulte d'autres ondes stationnaires qui se forment dans tout l'espace qui les sépare. Ce qui est remarquable, c'est que si la vitesse des électrons n'est pas la même, les ventres et les nœuds se déplacent à la vitesse intermédiaire "alpha". Tout observateur qui se déplacerait à cette vitesse alpha verrait donc les deux électrons s'éloigner ou se rapprocher tous les deux à la même vitesse.
On parle ici des champs de force, qui sont à la base de la véritable "mécanique ondulatoire". On peut par exemple citer le champ de force électrostatique:
Le champ de force électrostatique, dit « biconvexe ». Si les électrons se déplacent, cette structure adopte aussi le comportement des ondes d'Ivanov.
Le « Principe d'action et de réaction » découvert par Galilée et formulé par Newton.
Du point de vue du champ de force, considérant la vitesse alpha, on peut parler plutôt d'un « Principe de double action ». De ce point de vue il se produit plus simplement deux actions de force égale mais de sens opposé.
Le médium virtuel Delmotte-Marcotte. Sachant que le "lagrangien" est donné par la différence entre l'énergie cinétique et l'énergie potentielle, on peut facilement détecter la présence d'ondes stationnaires en travaillant avec le médium virtuel Delmotte-Marcotte. C'est d'ailleurs M. Marcotte lui-même qui a montré comment procéder. Le résultat est remarquable et même spectaculaire. Voici par exemple un programme FreeBasic qui permet de faire apparaître le champ de force que j'appelle "plano-convexe", qui est fait d'ondes stationnaires créées par l'addition des ondes progressives provenant de deux émetteurs, l'un produisant des ondes planes et l'autre, des ondes circulaires: Wave_Algorithm_Template.bas Wave_Algorithm_Template.exe Appuyez sur "C" pour faire apparaître les ondes stationnaires. Vous pouvez déplacer les émetteurs avec la souris et modifier les paramètres à votre gré. Ce programme étant relativement simple, il permet de se familiariser avec les ondes virtuelles modélisées sur ordinateur. Vous pouvez le copier, le distribuer et même le modifier à votre gré. J'ose espérer qu'il sera utile à tous ceux qui souhaitent étudier ce fantastique médium virtuel – et aussi les ondes stationnaires! Par la suite, vous pourrez examiner tous les programmes suggérés un peu partout sur ce site pour mieux maîtriser des phénomènes comme la réflexion dite "dure" ou "douce", la diffraction Fresnel-Fraunhofer et même la tache d'Airy. Je suis d'ailleurs persuadé qu'un jour prochain, on arrivera à reproduire le fonctionnement d'un électron et même la structure d'un proton de cette manière. J'insiste sur le fait que leur structure, ainsi que celle du noyau de l'atome, de l'atome dans son ensemble et même celle des liaisons chimiques font précisément toutes appel à la tache d'Airy et à la diffraction de Fresnel. C'est tout à fait normal et prévisible puisque la matière, étant faite d'onde, présente forcément une structure ondulatoire. Il faudra le faire en trois dimensions, ce qui exige que l'ordinateur soit doté de beaucoup de mémoire. Il faudra aussi le faire en langage C en tirant parti au maximum des grandes possibilités des cartes graphiques et du calcul en parallèle.
La tache d'Airy, selon l'angle d'ouverture. Les protons et les neutrons du noyau atomique s'assemblent sur les trois axes de Descartes en respectant cette structure.
La diffraction de Fresnel. Le noyau des atomes produit ce phénomène de diffraction sur les trois axes de Descartes. Chaque zone sombre située sur l'un des axes correspond à une couche atomique et peut capter un électron. Il en résulte huit (8) zones intermédiaires qui justifient les 8 électrons périphériques responsables des liaisons chimiques.
Et il faudra surtout mettre au point un algorithme plus élaboré qui tienne compte à la fois de la rigidité et de la densité du médium. Il est essentiel que le médium soit non dispersif (l'air est non dispersif alors que le CO2 l'est). On sait par exemple que l'hélium transmet le son beaucoup plus rapidement que l'air en raison de sa faible densité. L'air est expansible indéfiniment, de sorte que la pression "nulle" est en réalité la pression moyenne. Toute pression négative correspond dans les faits à une pression positive mais inférieure à la moyenne. Elle est donc limitée par un seuil inférieur infranchissable limitant ainsi l'amplitude possible d'un son. Les liquides possèdent une certaine viscosité. Les corps solides transmettent au contraire des sons dont la phase négative correspond effectivement à une pression négative. Il faudra faire appel à certaines de ces propriétés pour reproduire le phénomène de l'amplification des électrons et des champs de force à l'aide de l'énergie des ondes qui se propagent dans les environs. C'est dû au fait que la vitesse des ondes varie selon ces paramètres et que les ondes stationnaires, en compressant localement le médium, ont une influence certaine sur les ondes progressives qui les traversent, et réciproquement. L'amplification des ondes stationnaires. En supposant que les pertes soient nulles et que les ondes se déploient dans un espace fermé, les ondes stationnaires sont stables et elles continuent de vibrer indéfiniment. Mais il se produit des pertes si une partie de l'énergie est rayonnée. Dans le cas de la matière, qui rayonne sans cesse des ondes, il se produit effectivement de telles pertes. Toutefois, puisque l'éther est rempli d'ondes qui circulent dans toutes les directions, chaque électron et chaque champ de force peut utiliser l'énergie de ces ondes pour s'alimenter en énergie. D'une part, à l'intérieur des ondes stationnaires, chaque nœud de pression se comporte comme une lentille. Il fait dévier toute onde qui le traverse. L'énergie dispersée est très faible, mais l'effet est cumulatif et il devient déterminant s'il se répète sur des millions de longueurs d'onde. D'autre part, toute onde qui pénètre à l'intérieur de ces ondes stationnaires dans le même sens est progressivement accélérée ou ralentie selon que ses fronts d'onde sont en phase ou non avec les ventres et les nœuds. Tout indique qu'elles se retrouvent finalement en phase peu importe leur période initiale, de sorte que ces ondes entrantes contribuent directement à l'amplification d'un système stationnaire... |
I – Les deux trains d'ondes ont la même intensité et la même longueur d'onde.
|
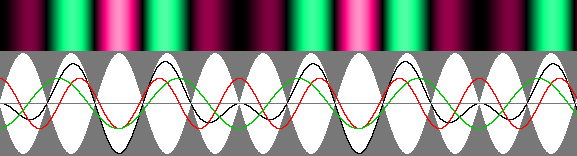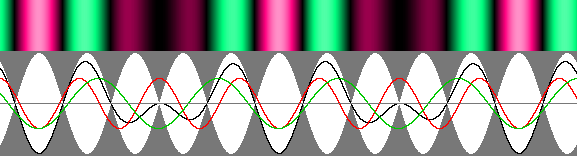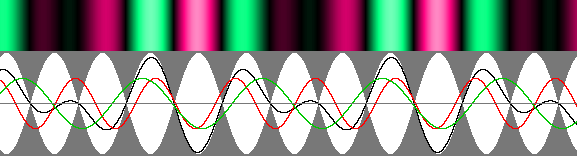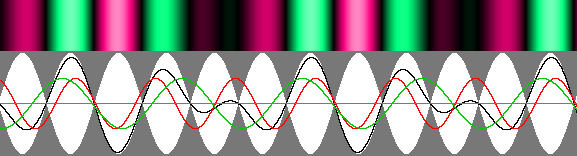
Peu d'auteurs mentionnent qu'il existe toute une variété d'ondes stationnaires. Il faudra évaluer dans cette page les effets d'un changement dans la fréquence, l'amplitude et l'orientation des deux composantes. On s'en tiendra aussi aux ondes stationnaires planes en gardant à l'esprit qu'il existe des ondes stationnaires sphériques qui elles aussi ont la propriété de se déplacer et de se contracter sensiblement de la même manière. Si les deux trains d'onde qui circulent strictement en sens opposé ont la même intensité et la même fréquence, le système est véritablement "stationnaire". Il se forme des ventres et des nœuds de pression, mais on peut tout aussi bien parler de ventres et de nœuds de courant en considérant le déplacement des particules constituant la substance du médium qui véhicule les ondes. Les nœuds de pression correspondent aux endroits où la pression ne varie pas. Leur emplacement est fixe, alors que celui des ventres de pression alterne deux fois par période aux demi-longueurs d'onde selon que la pression locale atteint un maximum ou un minimum qui déterminent l'amplitude de l'ensemble. Deux fois par période, la pression du médium est uniforme partout et elle correspond à une moyenne, qui peut être indifféremment positive, négative ou nulle. Mais à ce moment la substance de ce médium se déplace dans un sens ou dans l'autre en direction du futur ventre de pression. C'est ce qui permet d'envisager plutôt des ventres et des nœuds de courant et donc la présence d'énergie cinétique. Le tout se déroule (apparemment en tous cas) selon les lois de Newton, sachant que toute oscillation obéit également à la loi de Hooke: "Telle extension, telle force". On peut parler d'énergie potentielle en considérant les nœuds et les ventres de pression. L'énergie cinétique a plutôt un lien avec les nœuds et les ventres de courant, donc avec le mouvement des particules ou de la substance qui constituent le médium. Il faut remarquer que ces deux formes d'énergie alternent dans le cas des ondes stationnaires alors qu'elles évoluent l'une à la suite de l'autre à la quadrature dans le cas des ondes progressives. L'exception qui confirme la règle: les ondes véritablement stationnaires. L'animation ci-dessous montre, dans la partie du haut, deux courbes mobiles qui indiquent la pression à l'intérieur des deux trains d'ondes impliqués, du moins d'un point de vue mathématique. La courbe noire indique le total des deux, les déplacements de cette courbe étant limités à une enveloppe fixe caractéristique affichée en blanc. Dans la partie du bas, on a traduit la courbe noire en échelle de gris. Ce procédé mixte montre plus clairement ce qui se passe à l'intérieur des ondes stationnaires. |

Les ondes stationnaires normales: bêta = 0.
Les ventres et les nœuds sont véritablement "stationnaires" et la longueur d'onde est inchangée.
|
Il faut souligner en particulier que ce système ne transporte pas d'énergie, qu'elle soit cinétique ou potentielle, car la substance du médium demeure parfaitement immobile à l'emplacement de chaque nœud. Elle ne fait que rebondir d'un nœud à l'autre. L'énergie cinétique est convertie en énergie de pression et de nouveau en énergie cinétique dans un cycle théoriquement sans fin semblable à celui du pendule. Il s'agit d'un calcul relativement simple basé sur la loi de Hooke. Le calcul d'une onde progressive est beaucoup plus complexe. M. Anselme Dewavrin a montré qu'on peut considérer que les algorithmes mis au point par M. Philippe Delmotte et M. Jocelyn Marcotte font appel à la méthode d'Euler. Leur version simplifiée permet en particulier de retrouver le sinus et le cosinus de n'importe quel angle et même tout l'échelle avec une précision surprenante à la condition que ces algorithmes démarrent avec une constante que j'ai appelée la "constante de Dewavrin": 2 * Sin(pi / lambda). On aurait pu s'en douter puisque les ondes élémentaires sont sinusoïdales. En voici la preuve. WaveMechanics01.bas WaveMechanics01.exe Cela indique que les ondes stationnaires ne contiennent pas réellement d'ondes progressives qui se propagent en sens contraire. C'est bien ce que le calcul mathématique donne à penser, mais ce calcul ne correspond absolument pas aux faits. Il est vrai que les ondes stationnaires rayonnent les ondes qu'elles sont censées contenir si au moins l'un des deux écrans qui les limitent est enlevé brusquement, mais le processus qui justifie ce comportement peut tout aussi bien être expliqué par une réflexion. Je suis formel là-dessus: l'énergie de deux trains d'ondes progressives identiques qui se rencontrent dans un espace libre et qui forment des ondes stationnaires est incapable de les traverser. Elle retourne d'où elle vient et il se produit donc une réflexion dès le premier nœud rencontré. J'ai pris la peine de montrer ce résultat théorique dans la partie inférieure de la vidéo ci-dessous. La partie supérieure montre l'équivalent qu'on peut obtenir à l'aide du médium virtuel Delmotte-Marcotte. On voit très bien que l'addition de l'amplitude de deux trains d'ondes circulant en sens opposé s'additionne et permet de reproduire même les ondes d'Ivanov si la longueur d'onde n'est pas la même dans les deux sens. Standing_Waves_02_Theoretical.mkv Il est faux de prétendre que les ondes stationnaires contiennent des ondes progressives. On dira que le résultat est le même, mais ce n'est pas toujours vrai. Je répète que chaque nœud qui se forme entre deux ventres de courant constitue un obstacle infranchissable. Ce point étant constamment à zéro, il est très clair que l'énergie des ondes ne peut pas le franchir. D'ailleurs, ceux qui auront l'occasion d'analyser la succession des échanges d'énergie ou de "potentiel" au sein même du médium virtuel Delmotte-Marcotte constateront que chaque nœud constitue effectivement un écran qui fait en sorte qu'il s'y produit une réflexion dite "douce". On peut en effet y placer un miroir plan à réflexion douce sans constater la moindre différence. En outre, il se produit très certainement une réflexion dite "dure" sur le noyau central des ondes stationnaires sphériques puisqu'on y observe l'inversion de phase caractéristique de ce type de réflexion. Exceptionnellement, le ventre de pression sphérique situé au centre mesure une onde entière de diamètre et non pas la demi-longueur d'onde habituelle. C'est ce que montre le diagramme ci-dessous, qui a été obtenu en faisant la sommation de milliers d'ondelettes de Huygens réparties uniformément sur la surface interne d'une sphère parfaite. Autrement, les ondes qui réussiraient à traverser ce noyau se retrouveraient en opposition de phase avec les ondes divergentes qui se situent du côté opposé et elles provoqueraient leur annulation pure et simple par interférences destructives...
Les ondes stationnaires sphériques.
Et enfin, on peut voir ci-dessous que si l'amplitude des ondes provenant d'une direction privilégiée est supérieure, le déséquilibre a pour effet de déplacer ce nœud et donc tout le noyau central. Ce phénomène nous permettra d'y voir un peu plus clair sur le mécanisme réel de la pression de radiation exercée par les champs de force. C'était donc une erreur grave de prétendre que les ondes stationnaires sont faites de deux trains d'ondes circulant en sens opposé. Nous savons maintenant que les ondes progressives peuvent exercer une influence sur les ondes stationnaires sphériques. La physique actuelle véhicule un grand nombre d'erreurs de ce genre. Malheureusement, chacune d'entre elles conduit à un cul-de-sac et constitue un obstacle à toute nouvelle découverte. La vérité, c'est que les ondes stationnaires agissent et réagissent entre elles. Elles se comportent en cela comme le fait la matière. Il n'en faut pas plus pour comprendre que la matière est constituée d'ondes stationnaires.
II – La longueur d'onde n'est pas la même dans les deux sens. Nous abordons ici l'aspect le plus intéressant des ondes dites "stationnaires", ces mal nommées puisqu'elles peuvent tout aussi bien se déplacer. Paradoxalement, elles sont pourtant méconnues. Voici donc ce qui se passe si la longueur d'onde n'est pas la même dans les deux sens:
Les ondes stationnaires d'Ivanov. On a ici une vitesse alpha de 0,2 (g = 0,979796) avec des longueurs d'onde de 80 et 120 pixels. La longueur d'onde est comprimée à 96 pixels : lambda' = g * moyenne géométrique = g2 * moyenne arithmétique. Cette vitesse plus lente permet de mieux observer l'onde de phase, qui défile vers la droite à 5 fois la vitesse de la lumière.
Il était difficile autrefois de faire la preuve que ces ondes se comportaient bien ainsi. Mais depuis que nous disposons du médium virtuel Delmotte-Marcotte, j'ai pu en faire des séquences vidéo tout à fait convenables. Tel que promis, vous pouvez y observer le déplacement et la contraction de la structure typique des ondes stationnaires, avec ses "ventres" et ses "nœuds". On peut surtout y observer beaucoup mieux l'onde de phase dont parlait Louis de Broglie. La vitesse de cette onde de phase est toujours supérieure à celle de la lumière. Elle vaut c / alpha (1 / alpha si l'on pose c = 1) et sa longueur d'onde correspond à lambda' / alpha. La vidéo montre également les formules qui sont utiles pour démêler tout ça. Je me suis employé à les simplifier au maximum tout au long de ces années, de sorte que vous n'y trouverez aucune intégrale... Les transformations Alpha. J'ai indiqué plus haut que les ondes d'Ivanov correspondent aux transformations dites Alpha, qui peuvent être déduites des transformations de Lorentz moyennant quelques modifications mineures. On pourrait parler des "transformations transformées" de Lorentz, mais puisque celles-ci font état d'une vitesse normalisée alpha, il vaut mieux parler des transformations Alpha en précisant que c'est le précalcul et la définition des variables x et t qui font toute la différence. En général, personne ne réalise qu'avant d'appliquer les transformations de Lorentz au moyen d'un ordinateur, il faut effectuer un précalcul sur un pixel donné pour évaluer son "espace", c'est à dire ses coordonnées x et y (exprimées ici en longueurs d'onde correspondant à la moyenne géométrique), et le "temps" t (ici en "pulsations" ou périodes d'onde) qui règne en maître sur l'ensemble. Bien évidemment, c'est nécessaire avant même de penser à obtenir les variables modifiées x' et t'. Il est essentiel de savoir de quoi on parle pour que l'image affichée sur l'écran corresponde bien aux ondes qu'on désire montrer. De plus, puisque nous disposons aujourd'hui des ordinateurs, il n'est plus nécessaire de faire cette démonstration en recourant aux équations de Maxwell...
Les transformations Alpha s'appliquent aux ondes d'Ivanov : elles n'ont rien à voir avec la Relativité. On verra plus loin que les mêmes équations s'appliquent pourtant à l'électron et à la matière. Mais alors elles impliquent un ralentissement de la fréquence qui conduit tout droit à la Relativité.
J'ai bien sûr réalisé une vidéo qui montre que ces équations fonctionnent vraiment. Si vous vous donnez la peine de vérifier le code source, vous verrez bien que j'ai utilisé ces équations pour produire les ondes stationnaires de la partie inférieure. Standing_Waves_03_Transformations.mkv Standing_Waves_03_Transformations.bas Ces transformations dites Alpha ont une incidence majeure sur la structure de la matière et sur ses mécanismes parce qu'elles affectent aussi les champs de force. Ceux-ci sont faits d'ondes stationnaires plus complexes, mais qui présentent toutefois les mêmes caractéristiques que les ondes d'Ivanov. Je montrerai éventuellement qu'il s'agit d'un aspect parallèle et tout à fait négligé des transformations de Lorentz, car elles conduisent à la même "invariance" caractéristique. Voici une séquence qui montre la formation du champ de force électrostatique entre deux électrons dont l'un se déplace à 0,707 fois la vitesse de la lumière, l'autre étant au repos.Est-il
besoin de rappeler que ce sont principalement ces
champs de force qui contiennent l'énergie utile de la matière.
Leur étude s'avère donc primordiale.
Un exemple : la moitié de la vitesse du son ou de la
lumière. L'animation
ci-dessous montre comment ces ondes se comportent dans un
référentiel qui se déplacerait à 0,5 fois la vitesse du son. On a
donc alors bêta = 0,5.
Si la longueur
d'onde diffère, les ondes dites "stationnaires"
ne sont plus stationnaires. La vitesse
de déplacement des ventres et des nœuds correspond au rapport
des longueurs d'ondes. De plus, les
ventres et les nœuds se contractent. Que ce soit à cause de l'effet Doppler ou non,
et qu'il soit relativiste ou non, les ondes progressives qui se
propagent vers l'avant sont ici trois fois plus contractées que celles qui
se propagent en sens contraire. En effet, le rapport des longueurs d'onde
est donné par: R=(1+bêta)/(1–bêta)=3.
Si on suit les nœuds dans leur déplacement, les ondes qui se
propagent vers l'avant semblent aussi se déplacer
trois fois plus lentement. Avant toute chose, il faut établir très clairement que si un observateur se déplace à la même vitesse que celle des ventres et des nœuds de ces ondes stationnaires, soit dans notre exemple à la moitié de la vitesse du son, des notions comme la longueur d'onde et la fréquence n'ont plus la même signification. Il faut aussi rappeler que le son ne se comporte pas comme la lumière ou les ondes radio parce que la fréquence des émetteurs en mouvement ne ralentit pas. D'une part la longueur d'onde n'est pas la
même vers l'avant (vers la droite par convention, bêta étant alors
positive) que vers l'arrière. Une manière de mesurer la fréquence (plus
exactement la
cadence) consiste à recourir au test de Hertz (un microphone et un écran plat)
ou à un interféromètre. Alors la différence disparaît car on mesure
en réalité la
distance entre les nœuds qui se forment. Il faut compter deux nœuds
par longueur d'onde puisqu'ils se succèdent aux demi-ondes. D'autre part,
puisque le
microphone se déplace lui aussi à la vitesse des ventres et des nœuds, ces ondes
dont la fréquence et la longueur diffèrent l'atteignent pourtant selon la même cadence. C'est qu'il existe un effet Doppler
"relatif" qui doit être attribué au déplacement du
récepteur. Je répète ici que ce phénomène avait été signalé
dès 1842 (donc exactement un siècle avant ma naissance!) par Christian Doppler lui-même. Cette notion de
"cadence"
qu'on oublie trop souvent s'avère donc capitale, et ceux
qui n'en sont pas convaincus devraient jeter un coup d'œil à la page
sur l'effet Doppler.
Il
est très rare qu'on produise délibérément de telles ondes
stationnaires Ivanov en émettant des ondes progressives qui circulent en
sens opposé et dont la fréquence n'est pas la même. Le plus souvent,
le phénomène se produit automatiquement quand tout le dispositif
émetteur se déplace
comparativement au médium. Dans ce cas, les miroirs mobiles d'un
interféromètre ou l'unique écran du test de Hertz produisent un
effet Doppler. Or il existe un effet Doppler relativiste caractérisé
par un ralentissement de la fréquence, de sorte que le son et la
lumière ne se comportent pas de la même manière. Toutefois, le rapport
des longueurs d'onde R est le même dans les deux cas pour une vitesse
donnée. Voici
un tableau qui permettra d'y voir plus clair : |

L'effet Doppler.
À droite, l'effet Doppler relativiste se distingue à cause du ralentissement de la fréquence selon Lorentz : f ' = g * f.
Supposons que la longueur d'onde (lambda) est de 4 mètres lorsque l'émetteur est au repos et qu'il s'agit d'un son.
On aura par exemple, avec un seul émetteur en mouvement : bêta = 0,5 avec g = racine(1 – bêta2) = 0,866.
Le test de Hertz (un écran plat et un microphone, tous deux également en mouvement) révélera une contraction des ondes stationnaires :
Sur l'axe du déplacement (x) : lambdax = g2 * lambda = 3 m.
Sur un axe orthogonal (y) : lambday = g * lambda = 3,4641 m.
Supposons maintenant qu'un émetteur est au repos et qu'un deuxième émetteur s'éloigne vers la droite à 0,5 fois la vitesse du son.
Entre les deux, on a : lambda = 4 vers la droite et lambda2 = lambda * (1 + bêta) = 4 * (1 + 0,5) = 6 m vers la gauche.
On obtient des ondes stationnaires Ivanov dont la vitesse est donnée par : alpha = (6 / 4 – 1) / (6 / 4 + 1) = 0,2 m.
Même s'il s'agit d'un son, le tableau ci-dessous permet aussi de trouver la longueur d'onde de ce système :
lambda' = racine(lambda * lambda2) = racine(4 * 6) = 4,899 m.
Mais s'il s'agit de la lumière ou des ondes radio, le test de Hertz (un écran métallique plat et une antenne) produit des résultats différents :
Contraction sur l'axe du déplacement : lambdax= g * lambda = 3,5641 mètres.
Pas de contraction sur l'axe transversal : lambday = lambda = 4 mètres.
C'est dû au fait que la fréquence diminue selon le facteur g.
Et puisque la matière se contracte aussi selon g sur l'axe du déplacement, la contraction de ces ondes stationnaires est invérifiable !

LA CONTRACTION DES ONDES D'IVANOV PAR EFFET DOPPLER ACOUSTIQUE
|
Considérons maintenant un système acoustique qui serait produit par deux haut-parleurs mobiles situés sur l'axe du déplacement et alimentés à la même source. La distance qui les sépare étant constante, ils produisent tous les deux le même effet Doppler selon : lambda prime = lambda * (1 – bêta) vers l'avant et lambda prime = lambda * (1 + bêta) vers l'arrière. Il s'agit bien sûr du dispositif mis au point par M. Yuri Ivanov en 1990. C'est ce que montre la vidéo suivante dans la partie supérieure. On voit très bien que les ventres et les nœuds se déplacent exactement à la même vitesse que les émetteurs. La longueur d'onde étant établie en pixels, et puisque les ondes se propagent dans un médium virtuel qui ne trompe pas, il est aujourd'hui plus facile de vérifier que les observations de M. Ivanov étaient justes. Par contre, puisque la contraction sur l'axe du déplacement se fait selon le facteur g au carré, il faut convenir que ce résultat est différent de ce que montre la partie inférieure. En effet, dans le cas de l'électron, de la lumière et des ondes radio, la contraction est moins sévère puisqu'elle se fait selon le facteur g simple. On peut aussi montrer le système tel qu'il apparaîtrait s'il était observé par quelqu'un qui se déplacerait à la même vitesse que les ventres et les nœuds. Bien évidemment, selon le Principe de Relativité de Galilée, ces ventres et ces nœuds lui apparaîtraient de nouveau "stationnaires": |

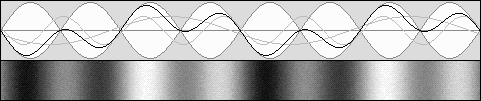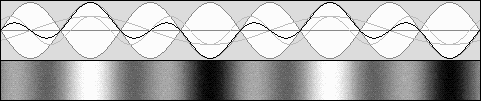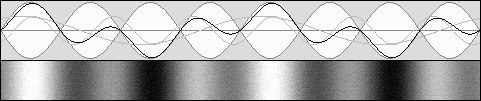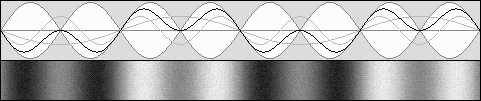
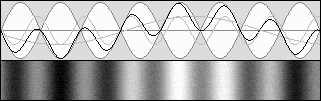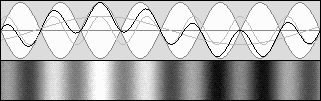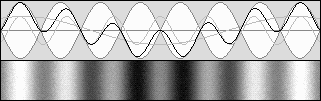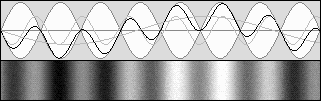
En haut, le système acoustique est au repos : on a donc bêta = 0 et la contraction est nulle.
Au centre, avec bêta = 0,5 et g = 0,866, les ondes sonores sont "apparemment stationnaires" et elles se contractent de 75% selon g2
Le diagramme du bas montre qu'à 0,707 fois la vitesse du son, avec g = 0,707 également, la contraction atteint 50% selon g2
Il faut comprendre que l'observateur se déplace vers la droite à la même vitesse que les ventres et les nœuds.
Les ondes qui circulent vers la droite semblent se déplacer plus lentement puisqu'il s'agit de leur vitesse relative.
LE TEST DE HERTZ MODIFIÉ ET L' EFFET DOPPLER ACOUSTIQUE
|
Il est très important de comparer les résultats obtenus plus haut avec deux hauts parleurs mobiles en considérant plutôt un système acoustique qui serait produit par deux haut-parleurs au repos et alimentés à la même source. Bien évidemment, il ne se produit plus d'effet Doppler à la source puisque les haut-parleurs de bougent pas. Les ondes venant en sens opposé ont la même fréquence et la même longueur d'onde. Par contre, en interposant un écran réflecteur mobile entre les deux haut-parleurs, on obtiendra un effet Doppler en cascade. Lors de la réflexion sur l'écran mobile, la longueur d'onde s'en trouvera modifiée à deux reprises, donc d'une manière relativement sévère. Selon que l'écran plat s'éloigne ou se rapproche de la source, on assiste à une double dilatation ou à une double contraction des ondes. Il s'agit ici d'un dispositif différent de celui que M. Ivanov a évalué en 1990. Ce n'est pas non plus l'équivalent du test de Hertz parce que l'écran est mobile alors que les émetteurs sont fixes. La vidéo proposée ci-dessous montre les équations qui rendent compte de cet effet Doppler en cascade si particulier qu'on oublie généralement d'en parler...Ici encore, on voit très bien que les ventres et les nœuds se déplacent exactement à la même vitesse que l'écran. On a vu aussi que dans tous les cas, la contraction des ondes d'Ivanov se fait toujours selon la moyenne géométrique des longueurs d'onde. On a donc toujours ici la longueur d'onde d'origine d'une part et la longueur d'onde doublement modifiée d'autre part. |
LA CONTRACTION DES ONDES D'IVANOV PAR EFFET DOPPLER RELATIVISTE
|
On a vu que dans le cas du son, la contraction des ondes stationnaires axiales vaut le carré du facteur de contraction de Lorentz. Mais lorsqu'on étudie le comportement de la lumière et des ondes radio, il faut aussi tenir compte du ralentissement de la fréquence, qui se fait selon ce même facteur g. Cela produit l'effet Doppler dit "relativiste". C'est en effet ce que nous indiquent les transformations de Lorentz. Mais c'est aussi ce que nous indiquent les transformations Alpha montrées plus haut puisqu'on a: t' = gt. Supposons que la longueur d'onde est de 4 mètres si l'émetteur est au repos et qu'il s'agit d'une onde radio et non pas d'un son. On garde le même exemple : bêta = 0,5 avec g = racine(1 – bêta^2) = 0,866.L'effet Doppler dilate la longueur d'onde vers l'arrière : lambda1 = lambda * (1 + bêta) / g = 6,928 m. L'effet Doppler comprime la longueur d'onde vers l'avant : lambda2 = lambda * (1 – bêta) / g = 2,3094 m. Le rapport des longueurs d'onde est le même que dans le cas du son : R = 6,928 / 2,3094 = 3 Si la vitesse normalisée bêta est inconnue, ce rapport permettrait en principe de la détecter : bêta = (R – 1) / (R + 1) = 0,5 Le tableau montré plus haut indique qu'on pourrait aussi retrouver la longueur d'onde du système au repos. Le problème, c'est que l'effet Doppler ne peut absolument pas être détecté si l'observateur est en mouvement. Le test de Hertz (un écran métallique plat et une antenne) indique une longueur d'onde comprimée : lambda' = lambda * g = 3,464 m. Toutefois, puisque la matière aussi se contracte selon le même facteur g, l'observateur est incapable de mesurer cette contraction.
Il s'agit d'un fait nouveau. Cette contraction des ondes stationnaires est la clé qui ouvre toutes les portes. Elle permet d'expliquer la Relativité. Puisque la matière est faite d'ondes stationnaires, elle doit se contracter de cette manière. C'est pourquoi l'interféromètre de Michelson s'est contracté comme l'a montré Lorentz et qu'il n'a pas pu révéler le vent d'éther. Si Lorentz en avait été informé, il aurait été conforté dans sa conviction que l'éther existe et que la matière se contracte vraiment. Pour démontrer que les ondes de la matière ralentissent leur fréquence selon les chiffres proposés par Lorentz, on peut faire remarquer que même la fréquence de résonance d'un son "stationnaire" transversal qu'on établirait entre deux écrans plats et parallèles montés sur un véhicule en marche devrait ralentir selon la vitesse de ce véhicule. Ce ralentissement de la fréquence de résonance sur un axe perpendiculaire à la direction du courant d'air devrait se faire selon le facteur g de Lorentz, ce qui fait que la distance entre les nœuds demeurerait constante dans cette direction. Il faut considérer en effet qu'à cause du déplacement des écrans, la distance réelle parcourue par les ondes du son devient plus grande que la distance qui sépare les écrans. Chaque front d'onde s'incline alors selon un angle thêta valant: arc sin(v/c), comme le ferait un avion en présence d'un vent venant par le travers. C'est ce ralentissement de la fréquence d'émission, qui produit invariance de la longueur d'onde sur les axes orthogonaux, qui est la caractéristique fondamentale des transformations de Lorenz. F' = g F D'une manière plus générale, même le principe de Huygens appliqué à des ondes stationnaires en mouvement doit prendre en considération le fait que le trajet des ondelettes de Huygens est allongé. La vitesse de la lumière étant constante, un parcours plus long se traduit forcément par un ralentissement de leur fréquence. C'est pourquoi la contraction des ondes stationnaires de la matière sur l'axe de son déplacement se fait selon le facteur g de Lorentz, et non pas son carré. C'est aussi ce qui explique que la matière ne se contracte pas sur les axes orthogonaux y et z. Le phénomène de la contraction des ondes stationnaires est maintenant connu depuis plusieurs années. Mais le monde scientifique refuse toujours de le reconnaître, avec un entêtement surprenant puisque c'est facilement vérifiable et qu'il s'agit d'une découverte de la plus haute importance . Les textes qui traitent des transformations de Lorentz et de la Relativité n'en font aucune mention. Pourtant, il est notoire que Lorentz a emprunté ses équations, dont le but initial était d'annuler l'effet Doppler, à Woldemar Voigt. En les soumettant aux équations de Maxwell, il en est arrivé à sa propre version, là encore en considérant des ondes. De plus, les transformations proposées par Lorentz avaient principalement pour but d'expliquer le résultat nul de l'expérience de Michelson, qui fait intervenir un interféromètre. Il s'agit d'un appareil muni de miroirs où la lumière circule sur deux axes perpendiculaires, ce qui implique un trajet aller et retour. Dans ces conditions, les ondes se rencontrent et il en résulte forcément des ondes stationnaires. D'ailleurs, les textes qui traitent de cet interféromètre ne mentionnent pas non plus cette contraction des ondes stationnaires. Tous ne font que reproduire le calcul fait par Michelson, qui ne fait intervenir que la vitesse relative de la lumière.Lorentz avait raison. Il aurait suffit de le croire. D'une part la nature ondulatoire de la matière était un fait inconnu à l'époque de Lorentz. Ce n'est que beaucoup plus tard que Louis de Broglie l'a mise en évidence. D'autre part ces ondes que la matière cache possèdent sûrement les mêmes propriétés que toutes les ondes. Elles sont donc soumises à l'effet Doppler et à une contraction s'il s'agit d'ondes stationnaires, cette hypothèse ayant d'ailleurs été retenue par de Broglie. Il a même montré qu'il devait se produire une onde de phase dont la vitesse, donnée par 1/bêta, est toujours supérieure à celle de la lumière. Personne à l'époque de Lorentz n'a voulu croire que la matière se contracte vraiment. Henri Poincaré en particulier s'y est opposé vivement. Pourtant, l'explication de Lorentz était simple. Il aurait suffit de le vérifier. Personne en effet n'a songé à vérifier attentivement la théorie de Lorentz, ce qui est proprement consternant. En particulier, on peut facilement montrer que l'hypothèse de Lorentz appliquée à la procédure de réglage des horloges par signaux optiques (pourtant si chère à Poincaré) conduit véritablement au décalage horaire et donc aux heures locales indiquées par Lorentz. On voit très clairement que des observateurs qui appliqueraient cette procédure seraient incapables de mettre en évidence le décalage horaire qui s'ensuit. Or Poincaré propose avant 1905 une procédure qui produit des résultats différents parce qu'il ne tient jamais compte de l'hypothèse d'une contraction de la matière selon le facteur de contraction g de Lorentz. Il tient pas compte non plus du fait que les horloges devraient afficher l'heure à une cadence plus lente. Après 1905, il propose sa propre théorie qui fait intervenir une ellipse allongée et qui est inutilement complexe en plus d'être erronée puisqu'elle ne correspond pas à celle de Lorentz. M ais aujourd'hui tout est bien différent parce que nous connaissons beaucoup mieux les ondes stationnaires. Il est beaucoup plus facile de montrer que Lorentz avait raison. On peut désormais l'affirmer : |
|
Puisque la matière possède une nature et une structure ondulatoire, elle doit se transformer selon les prévisions de Lorentz. |
|
La vitesse alpha et l'expansion de l'univers. Ce site comporte depuis peu une nouvelle page sur le Big Bang relativiste. On sait que les astronomes et les astrophysiciens n'ont jamais voulu attribuer le redshift "relativiste" des galaxies très éloignées et donc très rapides à la Relativité. Ils préfèrent l'attribuer à "l'expansion de l'univers". C'est bien plus simple, en effet. Pourtant, je dirais pour ma part que la Relativité s'applique à tout en ce monde, et particulièrement à tout ce qui se déplace très rapidement. Je suis convaincu que tous les tests qu'on conduira dans le futur démontreront que seule une expansion de l'univers qui respecte les transformations de Lorentz et la Relativité peut s'expliquer logiquement. Ce qu'il faut réaliser, c'est que nous avons l'impression d'occuper une position fixe au centre de l'univers. De plus, cet univers présente (ou semble présenter) une étonnante uniformité quelle que soit la direction même à des distances qui frôlent les 14 milliards d'années lumière. Je n'en dirai pas plus ici puisque tout est expliqué à la page en question. Mais puisque la présente page traite des ondes stationnaires, je veux tout de même montrer que cette idée d'une "vitesse alpha" intermédiaire qui milite en faveur d'une expansion relativiste est très pertinente. En fait, toute expansion qui ne respecterait pas ce critère deviendrait perceptible et nous permettrait de nous situer dans l'univers. Bref, cette idée d'un "pudding au raisins" qui gonfle ne tient pas la route. J'espère que je me fais bien comprendre : pour qu'un observateur en mouvement ait l'impression que deux galaxies semblent s'éloigner à la même vitesse, il faut absolument que sa vitesse propre soit légèrement supérieure à leur vitesse moyenne arithmétique. Si on considère le cas le plus simple, soit une galaxie fixe et une autre qui s'éloignerait à la moitié de la vitesse de la lumière, la vitesse de la galaxie intermédiaire doit respecter la "suite Alpha", qui est basée sur la loi de l'addition des vitesses relativistes de Poincaré. Elle doit correspondre à 0,2679 fois la vitesse de la lumière et non pas 0,5 / 2 = 0,25. C'est à cette condition que les ondes stationnaires formées par des ondes provenant de deux galaxies situées de part et d'autre de l'observateur sembleront s'immobiliser. En voici la preuve : |
III – Les deux trains d'ondes n'ont pas la même fréquence ni la même intensité.
|
Puisque cette page traite des ondes stationnaires, il convient de signaler que si les ondes ont la même fréquence mais pas la même intensité, l'enveloppe typique des ondes stationnaires affecte une forme très particulière qui rappelle la cosse des fèves ou des pois. C'est la même forme qu'on retrouve ci-dessous, mais on n'étudiera pas cette hypothèse ici. Parce que c'est le cas général des électrons, il importe de montrer plutôt ce qui se passe dans le cas des ondes qui n'ont ni la même fréquence ni la même intensité. On a représenté ces ondes telles qu'elles devraient apparaître si on se déplaçait à la moitié de la vitesse de la lumière, comme on l'a déjà fait plus haut. Alors l'enveloppe en forme de cosse persiste mais elle se déplace tout comme celle des ondes d'Ivanov ordinaires. Cette étude justifie la pression de radiation par le fait que les nœuds qui forment les ondes stationnaires des électrons peuvent être accélérés ou ralentis par des ondes progressives. On observe en effet que ces nœuds sont partiellement déplacés comme s'ils étaient bousculés lorsque les ondes n'ont pas la même intensité. C'est très visible dans l'animation suivante, où l'amplitude des ondes dilatées ne vaut que 35% du total : |
|
|
Les ondes partiellement stationnaires : v = 0,5c ; A1 = 65 % ; A2 = 35 %.
|
Tout objet subit normalement la pression constante d'ondes qui proviennent de toutes les directions. La pression de radiation est la composante de toutes ces forces, mais elle peut être très puissante parce que les ondes qui en sont responsables proviennent des champs de force, qui ont la propriété de les faire converger. |
IV – Les ondes se déplacent apparemment sur un axe perpendiculaire.
|
Les ondes qui se propagent apparemment sur un axe orthogonal, si l'émetteur en mouvement, doivent forcément s'incliner selon un certain angle: thêta = arc sin(v / c) de manière à continuer de suivre cet axe. Je suis toujours étonné de constater que personne ne semble en être conscient. Il faut bien comprendre que, puisque cet axe orthogonal se déplace lui aussi, chacun des fronts d'onde doit le rattraper. Ce comportement a pour effet d'augmenter le temps nécessaire à ce front d'onde pour qu'il puisse effectuer un certain trajet, le délai additionnel correspondant au facteur g de Lorentz. On sait d'ailleurs que Michelson a pu mettre au point son interféromètre en comparant ce temps avec celui qui est nécessaire pour que les ondes puissent effectuer un trajet égal sur l'axe du déplacement. On peut comparer ce phénomène au comportement d'un avion qui devrait voler en présence d'un vent venant par le travers. C'est l'évidence même. Je propose donc ici quelques séquences qui ont été réalisées dans un autre but, mais qui ont le mérite de bien montrer ces ondes inclinées. On comprendra ensuite plus facilement qu'à cause de l'effet de ciseau, des ondes inclinées qui se propagent en sens inverse provoquent la formation d'une onde de phase dont la vitesse est supérieure à celle de la lumière, soit selon 1/bêta. Bien que ce ne soit plus l'onde de phase décrite par de Broglie, elle affecte le même comportement. Doppler_Lorentz_2D_transverse_Fresnel_diffraction.avi Parabola_Transverse_Doppler.mkv Michelson_Interferometer.5c.mkv Bradley_Aberration.5c_Scan.mkv
Des ondes inclinées selon arc sin (v / c). Imaginons deux trains immobilisés côte à côte sur des voies parallèles. Les wagons de ce train ayant des côtés plats, il est possible de provoquer entre eux des ondes stationnaires sonores. Puisque les nœuds se forment aux demi-longueurs d'onde, seuls les sons dont la longueur d'onde est un multiple exact de la distance séparant les wagons peuvent entrer en résonance. Mais Michelson a montré que si les deux trains se mettaient en marche en conservant le même espacement, la vitesse relative des ondes circulant entre eux devrait diminuer selon une "aberration" qui correspond au facteur g de Lorentz. Il a expliqué plus exactement qu'un nageur qui doit traverser une rivière en présence d'un fort courant ne peut le faire aussi rapidement qu'en l'absence de courant. En fait, l'air qui circule entre les wagons ne provoque qu'un ralentissement apparent de la vitesse du son, car ce dernier doit se propager selon un certain angle, soit arc sin (v/c), et donc parcourir une plus grande distance. C'est pourquoi la fréquence de résonance en est abaissée. C'est à cause de ce phénomène qu'il a pu concevoir son interféromètre, sachant que le ralentissement des ondes est plus sévère encore sur l'axe du déplacement, soit selon le carré de l'aberrtation. Beaucoup de lecteurs ayant eu du mal à me suivre, j'ai dû reformuler cette présentation de manière à montrer en premier lieu ce qui se passe (ci-dessous, à gauche) lorsque le train accélère vers la droite à 10 % seulement de la vitesse du son. On a alors bêta = 0,1. On peut encore distinguer les ondes qui font l'aller et retour entre les deux wagons. On peut aussi y distinguer les mêmes changements de phase qu'on a montrés plus haut, et qui se traduisent par une onde de phase. Sachant que les ondes se déplacent toujours dans la direction perpendiculaire à leur plan, elles doivent s'incliner de 5,74 ° (arc sin bêta) à cette vitesse comparativement aux flancs des wagons :
|
|
|
|
À gauche : 10 % de la vitesse du son. À droite, 50 %.
|
La partie de droite correspond plutôt à 50 % de la vitesse du son. On a alors bêta = 0,5 et l'angle d'inclinaison des ondes vaut : arc sin bêta ou 30 °. Étrangement, on a l'impression que le système se déplace horizontalement. C'est encore plus trompeur dans l'animation montrée ci-dessous. Il faut bien comprendre qu'en réalité, les deux trains d'ondes progressives (théoriques, puisque dans les faits il se produit une réflexion sur chaque nœud) se déplacent transversalement, mais plus exactement selon un angle de 30°. Contrairement à ce qu'on semble observer, l'animation ci-dessous montre donc des ondes inclinées de 30° qui font l'aller et retour entre les deux wagons, représentés par les bandes noires du haut et du bas. Ces ondes stationnaires très particulières affectent l'allure d'un damier qui se déplacerait latéralement. On aura vu que l'animation montrée ci-dessus à droite représente le même système : |

Les ondes stationnaires transversales dans un système en mouvement. Vitesse du système : 0,5 c.
Toutefois, les ventres et les nœuds suivent ici "l'onde de phase", dont la vitesse, soit 1 / bêta, est toujours supérieure à celle de la lumière.
Il ne s'agit pas d'une plaisanterie : les ondes stationnaires transversales se propagent réellement de cette manière.
Vous pouvez les observer beaucoup mieux dans cette animation (attendez que la réflexion des ondes sur les paraboles confocales ait lieu) :
|
Les ondes circulent donc apparemment le long d'un axe perpendiculaire mais elles suivent en réalité un axe incliné de 30° vers l'avant (ici, vers la droite) comparativement à l'air. Elles se déplacent à la vitesse du son mais leur vitesse apparente est réduite selon le facteur g qui vaut ici 0,866. L'air circule vers la gauche à la moitié de la vitesse du son, soit à 612 km/h. On pourrait donc tout aussi bien provoquer la formation d'ondes stationnaires semblables entre deux écrans plats parallèles fixes, à la condition de les placer dans une soufflerie où l'air circule à la vitesse de 612 km/h. Les ondes ne voyagent pas réellement sur un axe perpendiculaire à celui du déplacement de l'air. Leur vitesse relative en est ralentie. La fréquence de résonance de ce système, incluant celles de ses harmoniques s'il y en a, en sera elle aussi ralentie. Puisque la matière fonctionne à l'aide d'ondes stationnaires, on peut en déduire que ses mécanismes, et donc les horloges en particulier, en sont aussi ralentis si elle se déplace à grande vitesse, ce qui confirme les prévisions de Lorentz. Le ralentissement des horloges a bel et bien lieu, et par conséquent il est tout à fait absurde de parler d'un "ralentissement du temps".
Il faut comparer ceci avec les ondes transversales de l'électron à la même vitesse :
Les ondes transversales de l'électron respectent la même structure en damier.
Les ondes orthogonales ne circulent pas vraiment sur le même axe. On en conclut que les ondes d'Ivanov présentent un degré de difficulté additionnel si elles s'établissent sur un axe orthogonal en mouvement comparativement au médium qui véhicule les ondes. Chacun des fronts d'onde présente un angle de déviation s'il est rapporté à cet axe orthogonal. On identifiera ici cet angle par le symbole grec thêta car fort heureusement, on trouve que cet angle est le même que celui qui permet de retrouver la vitesse alpha en se basant uniquement sur la moyenne arithmétique comparée à la moyenne géométrique. C'est ce qu'on a déjà montré plus haut dans un tableau où la vitesse alpha vaut la moitié de la vitesse de la lumière. À cette vitesse, qu'on peut alors renommer bêta, l'angle thêta correspond bien à 30° et il peut tout aussi bien être donné par la formule suivante: thêta = arc sin (bêta).
Il convient de souligner qu'on assiste à un phénomène identique en observant le comportement des ondes stationnaires qui constituent les champs de force, mais qu'on y retrouve en plus tous les angles possibles entre 0 et 90°.
Le champ de force électrostatique. La vitesse de l'onde de phase transversale passe de l'infini à la vitesse de la lumière à mesure que l'angle augmente.
Et comme si ce n'était pas suffisant, ce champ de force peut lui aussi se déplacer à la même vitesse que les électrons qui les ont créés, ou encore à la vitesse intermédiaire alpha si la vitesse des électrons n'est pas la même. On comprendra que l'étude des champs de force s'avère relativement complexe. Je suis néanmoins absolument certain qu'à la seule condition de considérer que ce champ de force est au repos, ce que la loi de la Relativité permet, le phénomène de l'action et de la réaction se résume à un "Principe de double action". Alors il se produit plus simplement deux actions de force égale mais de sens opposé, comme ceci:
Le décalage horaire annule apparemment l'effet de damier. Les transformations de Lorentz font état d'un "temps local". Les horloges situées à l'avant accusent du retard sur celles qui sont à l'arrière selon l'équation: –bêta * x. Si par exemple l'ensemble se déplace vers la droite à la moitié de la vitesse de la lumière, la distance entre les deux étant de 0,866 seconde-lumière (soit selon x' = g * x avec x = 1 seconde-lumière), l'horloge située à droite accusera un retard de 0,5 seconde... Or on a vu que les ondes planes qui circulent dans les directions transversales à l'intérieur d'un référentiel mobile sont inclinées. Mais à cause de ce décalage horaire, les occupants de ce référentiel seront incapables de mettre cette inclinaison en évidence. S'il s'agit d'ondes stationnaires transversales, ils n'y verront que des ondes stationnaires normales, exactement comme s'ils étaient au repos. L'animation ci-dessous montre qu'une onde inclinée selon l'angle q, qui vaut ici 60° selon une vitesse de 0,866 c, ne semble plus inclinée aux yeux des observateurs C, D ou O qui sont placés sur un axe transversal. En effet, pour détecter cet angle, l'observateur C, par exemple, doit chronométrer le délai entre le moment où l'onde atteint les points A et B. Il a prévu que A et B, qui sont à égale distance, l'avertiront par radio du moment précis où l'onde les aura atteint. Or cette animation montre qu'il recevra l'information exactement au même instant : |
|
|
L'angle d'inclinaison d'une onde ne peut pas être détecté à l'intérieur d'un référentiel mobile.
|
Étonnamment le décalage horaire, ce fameux "temps local" mis en avant par Lorentz, correspond donc à la correction nécessaire pour que l'onde montrée ci-dessus ne semble plus inclinée. Cette démonstration montre que l'aberration stellaire découverte par Bradley ne dépend pas de la vitesse absolue mais uniquement de la vitesse relative. C'est ce qui explique que cette aberration soit exactement la même à l'aller et au retour, donc aux 6 mois, malgré le fait que la Terre se déplace sans doute à grande vitesse à travers l'éther. Cette anomalie avait mystifié complètement Augustin Fresnel, car il ne connaissait pas les transformations de Lorentz. La séquence ci-dessous a déjà été proposée plus haut : Bradley_Aberration.5c_Scan.mkv Et de nouveau, l'électron. La page suivante traite des ondes stationnaires sphériques et donc encore une fois de l'électron mobile, déjà décrit à la page précédente. Vous pourrez constater que ses ondes axiales et transversales se comportent exactement comme les ondes d'Ivanov, mais à la condition de tenir compte d'un ralentissement de sa fréquence selon le facteur g de Lorentz. Cet électron présente même l'onde de phase décrite par Louis de Broglie. Celle-ci est bien visible dans l'animation montrée ci-dessous, à droite. Cela constitue une preuve additionnelle que "l'onde de La Frenière", qui est faite d'ondes stationnaires sphériques mobiles, possède toutes les propriétés de l'électron.
Que ça vous plaise ou non, il s'agit bien d'un électron. C'est l'hypothèse la plus raisonnable à l'heure actuelle. En fait, il n'en existe aucune autre... |
| 01 | 02 | Vous êtes ici. | 04 | 05 | 06 | 07 | 08 | 09 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 |
|
Gabriel LaFrenière, Bois-des-Filion en Québec. Sur l'Internet depuis septembre 2002. Dernière mise à jour le 16 septembre 2010. Courrier électronique : veuillez consulter cet avis. La théorie de l'Absolu, © Luc Lafrenière, mai 2000. La matière est faite d'ondes, © Gabriel Lafrenière, juin 2002. |