La Relativité selon Lorentz.

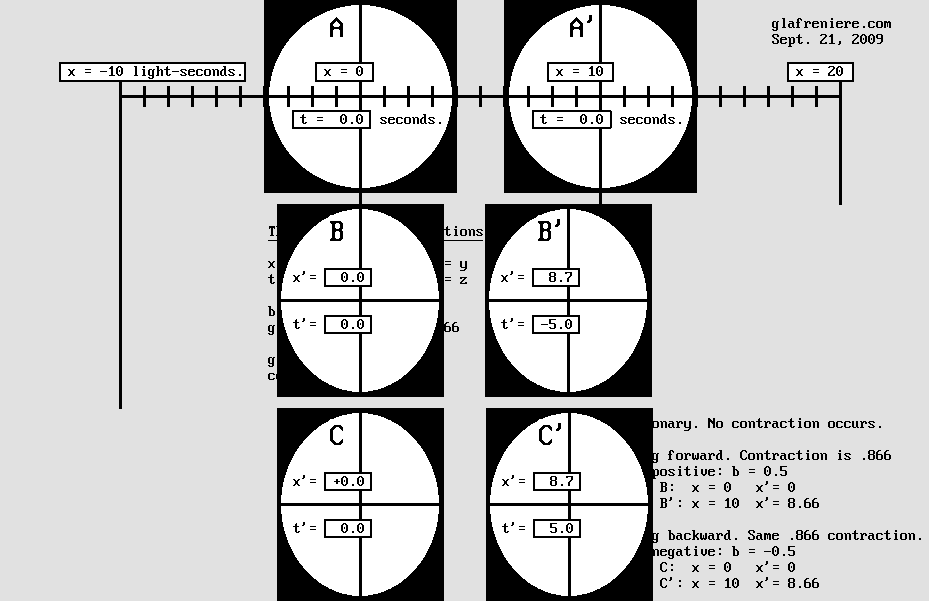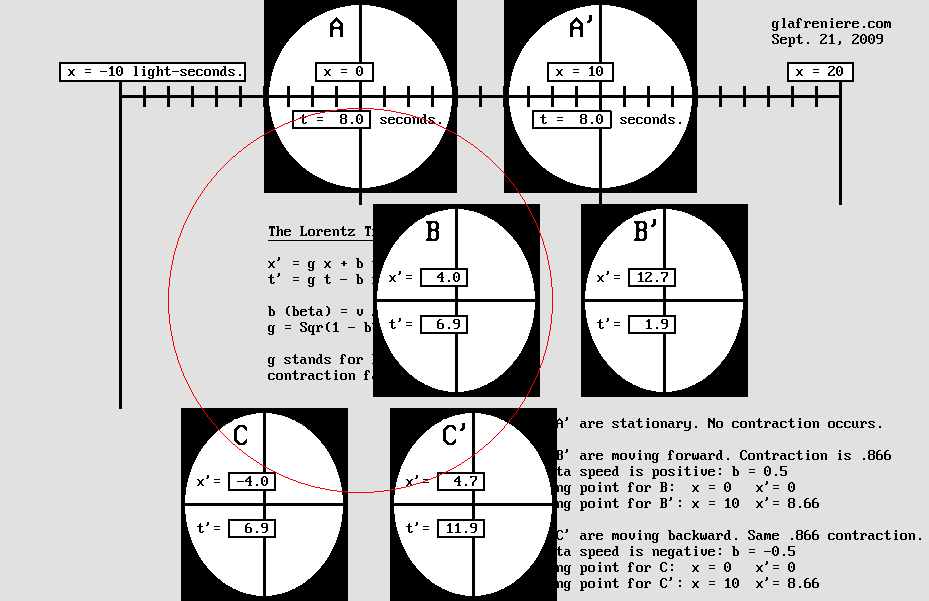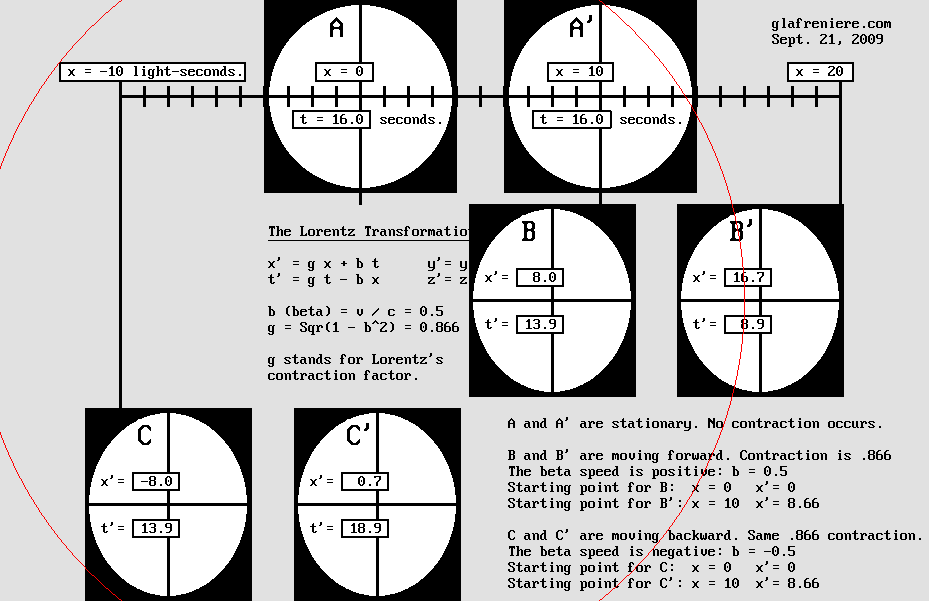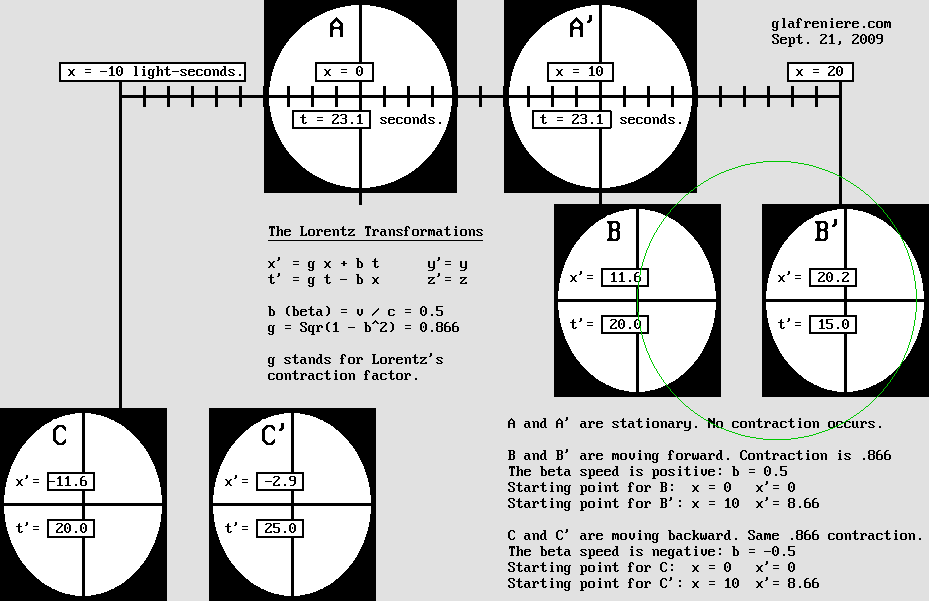
Au départ, les transformations de Lorentz avaient pour but d'annuler l'effet Doppler obtenu à l'aide des équations de Maxwell dans un référentiel mobile. Par la suite, Lorentz et Poincaré les ont utilisées pour rétablir les coordonnées d'un électron mobile de manière à ce qu'il apparaisse au repos. En inversant les équations de Poincaré, qui sont plus simples parce qu'il pose: c = 1 et bêta = v / c, on peut cependant obtenir l'effet inverse.

x' = g x + b t

t' = g t – b x

y' = y z' = z

Exemple : b (bêta) = v / c = 0,5

g (contraction) = Sqr(1 – b ^ 2) = 0,866

Contrairement à celui de Lorentz, ce groupe d'équations présente l'avantage immense de comporter des grandeurs x et x' absolues qui peuvent être reportées dans un unique référentiel cartésien présumé au repos dans l'éther. Il ne sera donc jamais question ici d'un référentiel "galiléen". De plus, il est bien plus transparent quant à ses effets, d'autant plus que c'est bien ce que Lorentz avait à l'esprit lorsqu'il a présenté ses équations en 1904. Voyez plutôt :

x' = g x + b t

1 – La matière se contracte selon g x. La distance convenue entre A et A' étant de 10 secondes-lumière, celle que B et B' respectent selon la même convention est plutôt de 8,66 secondes-lumière à cause d'une erreur dans leurs mesures. Ci-dessous, les carrés mesurant 8 secondes-lumière de côté se contractent en rectangles mesurant plutôt 8 x 6,9 secondes lumière. De même, les cercles deviennent des ellipses aplaties. Pour des raisons mécaniques, la contraction s'applique également aux espaces vides d'un système matériel complexe. En particulier, c'est à cause de cette contraction que l'interféromètre de Michelson devient incapable de mesurer notre vitesse à travers l'éther.

2 – Le point situé en g x passe en g x + b t puisqu'il se déplace à la vitesse de 0,5 c. Il s'agit tout simplement d'un mouvement de translation, connu en physique sous le nom de "Transformation de Galilée" et conduisant à son "Principe de Relativité". En inversant l'équation originale de la même manière qu'on l'a fait ci-dessus, on obtient : x' = x + v t au lieu de x' = x – v t.

t' = g t – b x

3 – Les horloges affichent des heures plus lentes selon : t' = g t. Ci-dessous, puisque g = 0,866, les horloges de B et de B' affichent 8,66 secondes après un délai réel de 10 secondes (0,866 * 10 = 8,66).

4 – Les horloges présentent un décalage horaire qui correspond à : – b x. Ci-dessous, l'horloge de B' est située à l'avant de celle de B. Elle est donc en retard de 5 secondes exactement sur elle, soit selon : – 0,5 * 10 puisque b (bêta) = 0,5. Il faut préciser que dans le cas de B', on a x = 10 secondes-lumière (x = 0 dans le cas de B).

Sachant cela, on peut finalement comparer comment réagiront les observateurs A et B. Commençons par le moment où ils se rencontrent sur la même coordonnée x = 0.

Les observateurs A et B sont en mesure de synchroniser leurs horloges selon t = t' = 0 puisqu'ils sont sur la même coordonnée x.

Puis l'observateur B' tente de synchroniser son horloge sur celle de B. Mais la procédure aboutit à un décalage horaire de – 5 sec.

B et B' tentent de maintenir une distance de 10 secondes-lumière. Mais la procédure aboutit à une distance de 8,66 secondes-lumière.

Voyons maintenant comment la situation aura évolué après un délai de 20 secondes.

La vitesse de l'observateur B étant de 0,5 c, il croise A' exactement au point : x = 10 secondes-lumière.

L'horloge de B fonctionnant plus lentement, elle affiche seulement : g * t = 17,32 secondes lentes au lieu de 20 secondes absolues.

L'observateur B n'a pas conscience que son environnement est contracté. De plus, il croit que A et A' se déplacent vers la gauche.

B pense que l'horloge de A fonctionne plus lentement puisqu'il constate à tort qu'elle affiche maintenant g * 17.32 = 15 secondes.

Étant parvenu à sa hauteur, B observe que l'horloge de A' présente un décalage horaire de + 5 secondes sur celle de A (15 + 5 = 20).

L'horloge de B affiche 17,3 secondes et c'est normal selon lui car la distance entre A et A' lui semble être de 8,66 secondes-lumières.

L'observateur B en vient à la conclusion qu'il est au repos et que ce sont plutôt A et A' qui se déplacent vers la gauche à 0,5 c.

Ses mesures étant exactes, l'observateur A en vient bien sûr à la conclusion qu'il est au repos, B et B' étant en mouvement.

En définitive, personne ne peut savoir lequel se déplace vraiment.

La Relativité de Lorentz, c'est ça.

Pourquoi faire compliqué quand on peut faire simple ?

Les transformations de Lorentz inversées.

Si vous avez des doutes à propos de mes équations, et c'est bien légitime, voici comment Henri Poincaré était parvenu à simplifier les équations de Lorentz qui, on le sait, avaient été empruntées à Woldemar Voigt :

Ci-dessus, on a une copie du texte où Poincaré simplifie les équations de Lorentz et où la constante de Voigt l est toujours présente.

Ci-dessus, j'ai reproduit la transposition de M. Christian Marchal où l'on retrouve le facteur gamma et la vitesse normalisée bêta.

Et voici les formules originales de Lorentz, qui apparaissent bien plus obscures en comparaison.

En simplifiant, on a bien : x' = (x – v t) / g

Malheureusement, ces formules ont pour effet de créer un nouvel "espace-temps" incompatible avec le premier.

Il faut savoir que Lorentz avait établi le premier, ce qui fut confirmé plus tard par Poincaré, que la constante de Voigt "l" devait être égale à 1 de telle sorte qu'on pouvait l'éliminer de ces équations. C'est pourquoi la première équation de Lorentz se résume à ceci :

Selon Lorentz : x' = (x – v t) / g

Selon Poincaré : x' = gamma (x – b t)

Si donc l'inconnue est plutôt x, il faut faire :

x = x' / gamma + b t

Remplaçons ensuite le facteur gamma qui vaut 1 / g par le facteur de contraction g :

x = g x' + b t

J'ai constaté après d'interminables tâtonnements sur l'ordinateur que la variable t s'appliquait déjà au référentiel au repos, ce qui avait pour effet de créer un deuxième "espace-temps" tout à fait erratique. Il fallait à tout prix réunir les variables x et t de manière à ce que les deux s'appliquent au référentiel réputé au repos. De toutes façons, et c'en est la preuve, l'ordinateur montre sans l'ombre d'un doute que pour obtenir un effet Doppler, il est obligatoire de permuter x et x' :

x' = g x + b t

Le même raisonnement étant appliqué à l'équation du temps, on obtient :

t' = g t – b x

En voici la preuve, corroborée par le Scanner du Temps :

Doppler_Voigt_transformations.bas Doppler _Voigt_transformations.exe

Par exemple, après un délai de 20 secondes et en se référant au point x = 10 secondes-lumière, la vitesse normalisée bêta correspondant à la moitié de la vitesse de la lumière, on obtient pour B' :

x' = g x + b t = (0,866 * 10) + (0,5 * 20) = 18,66 secondes-lumière.

t' = g t – b x = (0,866 * 20) – (0,5 * 10) = 12,32 secondes.

Ce qui est remarquable, comme l'a démontré Poincaré, c'est qu'il suffit d'échanger les variables (x, x'; t, t') et le signe (– au lieu de +) pour retrouver la coordonnée x et le temps t initiaux :

x = g x' – b t' = 10 secondes-lumière.

t = g t' + b x' = 20 secondes.

Pourtant, la forme retenue par Lorentz fonctionne aussi, sachant qu'on a permuté x et x' (on a donc t et non t'):

x = (x' – b t) / g = 10 secondes-lumière.

J'insiste sur le fait que ces équations ont la propriété de produire un effet Doppler, ou de l'annuler si elles sont inversées. Dans ce cas, les coordonnées cartésiennes x, y et z doivent s'exprimer en longueurs d'onde et le "temps" t, en périodes d'onde. Ainsi donc, ce ne sont pas l'espace et le temps qu'on modifie en pratique, ce sont la longueur et la période des ondes. C'était d'ailleurs l'intention initiale de Voigt. Mais ses équations de 1887 présentaient des défauts graves en plus d'être imprécises à cause de la constante, que Lorentz a dû préciser - et ensuite éliminer après l'avoir trouvée égale à 1. D'abord, il n'était pas vraiment nécessaire de modifier "l'espace-temps". C'était même à éviter absolument. Grâce à mon ordinateur, en tentant de corriger l'effet Doppler, j'ai fini par me rendre compte que c'était le temps t qui était la cause de ce malentendu, car il s'appliquait au mauvais référentiel. Et enfin, le signe est négatif dans les deux équations de Lorentz alors que l'ordinateur indique qu'il doit être positif dans l'équation x et négatif dans l'équation t. Mais c'est sans importance car il s'agit sans doute simplement d'une convention différente applicable aux équations de Maxwell.

J'ai aussi découvert que si l'on désire conserver la constante de Voigt, elle doit se trouver au numérateur dans l'équation x' et au dénominateur dans l'équation t'. Il s'agit là d'une autre erreur grave. Il en ressort que les équations de Voigt comportaient pas moins de trois erreurs graves, sans compter une imprécision (la constante) et une anomalie (le signe). Correction faite, on obtient ceci :

Les transformations de Woldemar Voigt revues et corrigées.

Elles demeurent utiles car elles permettent de reproduire ou de corriger un effet Doppler à fréquence variable.

Dans le cas de l'effet Doppler normal, la constante k est égale à g de manière à maintenir la même fréquence.

Dans le cas de la lumière et des ondes qui composent la matière, la constante k est égale à 1 de manière à ralentir la fréquence.

Cela signifie que, dès qu'on est en présence d'un effet Doppler impliquant la lumière ou les ondes radio, par exemple celles qui sont émises par un satellite, il s'agit en soi d'un "effet relativiste". En effet, un observateur posté dans ce satellite ne verra aucun effet Doppler dans les ondes qu'il émet parce que tout son environnement se transforme de manière à compenser. Ainsi donc, les transformations de Lorentz ne représentent rien d'autre qu'un effet Doppler particulier impliquant un ralentissement de la fréquence de l'électron ou de tout autre émetteur selon le facteur g.

Il s'agit tout simplement de l'effet Doppler.

Ces faits ne sont pas discutables : les formules de Lorentz avaient seulement pour effet de corriger l'effet Doppler. Celles que je propose ci-dessous, qui s'inspirent de celles de Poincaré, produisent d'abord un effet Doppler, qu'on peut ensuite corriger en utilisant les équations symétriques montrées à droite. Cet effet Doppler implique un ralentissement de la fréquence selon le facteur g de Lorentz. Il ne s'agit pas d'une théorie puisque n'importe qui peut le vérifier.

J'ai écrit un programme FreeBasic qui le montre d'une manière simple, claire et précise :

Doppler_Voigt_transformations.bas Doppler _Voigt_transformations.exe

Vous pouvez même modifier la valeur de la constante de Voigt en appuyant sur A, B, C ou D au choix. L'absence de contraction sur les axes y ou z est évidente lorsque k = 1. En effet, selon Lorentz, on a y' = y; z' = z. Dans ce cas, la fréquence de l'émetteur diminue selon le facteur g. Vous pouvez vérifier dans le code source que j'utilise bel et bien les équations (corrigées et inversées) de Voigt indiquées ci-dessus et non pas celles de Lorentz.

C'est pourquoi je propose de remplacer les équations de Lorentz par celles-ci, qui s'inspirent de celles de Poincaré :

Le groupe complet des transformations de Lorentz revues et corrigées.

Qu'on ne s'y trompe pas, ces équations produisent des résultats différents.

En particulier, les variables x et x' s'appliquent au même référentiel cartésien réputé au repos dans l'éther.

Toutefois, les grandeurs obtenues correspondent bel et bien à ce que Lorentz, Poincaré et Einstein ont tous proposé.

En effet, même Albert Einstein prévoyait qu'un objet mobile devrait nous apparaître plus court, soit selon g x ci-dessus.

Il devrait aussi sembler se déplacer conformément à : + bêta * t.

Et enfin, tous s'entendent également pour affirmer que les heures ralentissent selon : g * t.

On peut donc s'étonner que personne depuis un siècle n'ait proposé ces formules...

Le Scanner du Temps fait mieux encore.

Voici une vidéo plus complète qui devrait vous intéresser au plus haut point. Elle contient tous les éléments qui permettent de démontrer que la version de la Relativité proposée par Lorentz en 1904 était correcte :

Time_Scanner.mkv

VLC Media Player est l'outil idéal pour visionner cette vidéo .mkv (Matroska) réalisée en haute définition (1280x720) grâce au codec Mpeg-4 de DivX selon le standard H-264 maintenant incontournable. Vous pouvez aussi télécharger toute la série des codecs possibles et imaginables gratuitement chez CCCP (un clin d'œil à l'ancienne URSS), la version gratuite de Zoom Player incluse. Et voici le programme FreeBasic qui a produit cette animation:

WaveMechanics07.bas

Vous pouvez constater que mon Scanner du Temps est l'outil idéal pour montrer comment l'observateur B voit les choses de son propre point de vue, c'est à dire en postulant qu'il est au repos. Il réalise donc ici la même chose que les équations proposées par Lorentz et Poincaré, à savoir remettre l'électron mobile dans un repère au repos. On voit aussi qu'il est possible de montrer un nombre illimité de référentiels, ce que la Relativité d'Einstein est incapable de faire à cause des mesures incompatibles. On voit encore que la règle graduée rouge ne subit aucune transformation de longueur. Cela démontre qu'il est ridicule d'invoquer une transformation de l'espace puisqu'elle ne s'applique pas dans certains cas.

Soyons clairs, l'espace et le temps ne se transforment pas. C'est la matière qui se contracte, et ce sont tous les mécanismes, y compris celui des horloges, qui fonctionnent plus lentement.

Et enfin, cette animation montre hors de tout doute qu'il s'agit bien de l'effet Doppler, car j'ai obtenu ce résultat sur les ondes produites par les deux émetteurs mobiles en utilisant purement et simplement mes équations montrées plus haut, ou encore à l'aide de mon Scanner du Temps.

Il se dégage de cette vidéo une magnifique harmonie qui ne devrait laisser personne insensible.

Non seulement Lorentz avait raison, mais désormais la Relativité s'explique. Il n'y a plus de paradoxes. Tout devient clair et logique. En pratique, la Relativité d'Albert Einstein est inapplicable. Il est essentiel d'établir un référentiel privilégié, représenté dans la vidéo par la règle rouge, et cette démonstration indique que certains choix sont préférables à d'autres. Seule, la Relativité selon Lorentz permet ces choix, en soulignant qu'elle oblige à revenir à l'hypothèse de l'éther. Même s'il ne peut être détecté, tout se passe en effet comme si l'éther existait et que la vitesse de la lumière en dépendait.

Et puisqu'il est uniquement question de l'effet Doppler, cela suggère fortement que la matière se comporte comme le font les ondes. En effet, les ondes stationnaires aussi se contractent. Tout dans la Relativité mène à cette conclusion: non seulement la matière est faite d'ondes, mais toute sa mécanique fait aussi appel à des ondes. Et ces ondes dont la vitesse est celle de la lumière ne peuvent exister que s'il existe un médium capable de les transmettre: l'éther. En définitive, de tout ce qui est matériel, il n'existe rien d'autre que l'éther...

Les transformations de Lorentz vont donc bien au-delà de la Relativité. C'est toute la mécanique de la matière qui est en cause et en conséquence, il faudra revoir en ce sens les lois de Newton et toute la physique dans son ensemble.