LA DYNAMIQUE DES CHAMPS DE FORCE

Ce diagramme représente deux boules de billard qui se heurtent à grande vitesse.
Noter la présence d'un champ de force intermédiaire, qui est ici essentiellement électrostatique.
Ce sont les champs de force qui permettent l'échange de l'énergie cinétique entre deux corps.
La dynamique des champs de force permet de réhabiliter la mécanique de Newton malgré la Relativité.
![]()
![]() Page d'accueil :
La
matière est faite d'ondes.
Page d'accueil :
La
matière est faite d'ondes.
|
On a parlé dans les pages précédentes de l'énergie cinétique, et il est apparu clairement que cette énergie pouvait être transmise d'un corps à un autre sous forme de matière par l'intermédiaire d'un champ de force. Comme son nom l'indique, cette énergie a pour effet de communiquer un mouvement à la matière. Autrefois, j'affirmais que toutes les forces étaient attribuables à des ondes ; c'est tout à fait juste, mais il y a mieux. On peut désormais unifier toutes les forces en affirmant qu'elles sont toujours attribuables à des champs de force. Au lieu de parler de la dynamique des ondes, il devient préférable de parler de la dynamique des champs de force. De son côté, Isaac Newton n'a fait qu'énoncer des lois. Il n'a rien expliqué et il a d'ailleurs admis : « Je ne feins pas d'hypothèses ». C'est précisément parce qu'il ignorait qu'il était en présence de champs de force qu'il devient nécessaire de revoir ses travaux. Il faut réhabiliter Newton. Il n'empêche que, fondamentalement, l'œuvre de Newton demeure tout à fait pertinente. Ce n'est pas ce que les physiciens actuels prétendent. À leurs yeux, Einstein a complètement éclipsé Newton. Aveuglés par sa célébrité, ils s'en remettent à des préceptes aussi absurdes et complexes qu'ils sont inexplicables. Ils n'ont même pas la décence d'admettre que les transformation de Lorentz et la Relativité sont l'œuvre commune de Hendrick A. Lorentz et de Henri Poincaré. Il s'agira dans cette page de montrer que les lois de Newton revues et corrigées s'accommodent à merveille des transformations de Lorentz et de la Relativité. D'une part, à la page sur l'énergie cinétique, on est parvenu à corriger l'équation de l'énergie cinétique de manière à tenir compte de l'augmentation de la masse. Et d'autre part on en est arrivé à la conclusion que la dynamique de la matière selon Newton ne peut se vérifier que si le référentiel choisi correspond au centre d'inertie commun de deux ou de plusieurs corps matériels en interaction, en vertu de la troisième loi de Newton revue et corrigée citée un peu plus bas. Observons par exemple comment une boule de billard en frappe une autre lors d'un « choc élastique ». Dans l'animation ci-dessous, sa vitesse initiale correspond à 86,6% de la vitesse de la lumière. Il est bien évident que ces boules ne résisteraient pas à un tel impact, mais supposons qu'elles soient indestructibles : |

Le choc élastique simple.
|
Au repos, la masse de chacune des boules est d'un seul kilogramme. En plus de montrer le choc, cette animation affiche les valeurs suivantes : les masses actives a et réactives r, la masse augmentée M, la vitesse normalisée bêta, la masse totale de l'ensemble T et enfin, la différence de masse delta qui se trouve stockée temporairement dans le champ électrostatique. Vu de cette manière, le déroulement d'un choc élastique ne correspond absolument pas aux lois de Newton. Il correspond plutôt à la mécanique de Lorentz, en supposant qu'il soit possible de connaître la vitesse absolue des boules à travers l'éther. Or Henri Poincaré a découvert que notre vision des phénomènes physiques était relative. Nous avons toujours l'impression d'être au repos dans l'éther même si c'est hautement improbable. De plus, nous avons l'impression que les corps matériels qui se déplacent à grande vitesse subissent les transformations de Lorentz, alors que ce pourrait tout aussi bien être l'inverse. Le problème, c'est que plusieurs observateurs dont la vitesse n'est pas la même perçoivent différemment le même phénomène, et cela conduit inévitablement à des conflits. Il faut adopter une convention. La mécanique des champs permet de concilier les différents résultats à la satisfaction de chacun en recourant à un arbitre impartial dont la situation est avantageuse et privilégiée. Elle permet aussi de simplifier les lois et les calculs en éliminant toute référence à la Relativité (même celle de Lorentz) et en revenant fondamentalement à la mécanique de Newton. Nous savons que la mécanique de Newton fonctionne bien si les vitesses sont faibles. Désormais elle fonctionnera aussi bien à des vitesses qui frôlent celle de lumière à deux conditions : 1. - Définir un référentiel privilégié. 2. - Tenir compte de l'augmentation de masse. La troisième loi de Newton sur l'action et la réaction doit être profondément remaniée :
La troisième loi de Newton refondue devient le principe de double action. Ces actions sont toujours attribuables au champ de force qui se situe entre les corps.
Cette loi définit un référentiel privilégié : celui du champ de force, qu'on peut situer arbitrairement au centre d'inertie commun. Pour que cette loi se vérifie, il faut que l'observateur soit situé dans ce même référentiel. Il est alors en mesure de communiquer ce qu'il aura observé à n'importe quel autre observateur dont la vitesse n'est pas la même, à leur satisfaction. Si l'observateur ne peut pas se situer dans ce référentiel, la loi de l'addition des vitesse de Poincaré ou mon scanner du temps permettent de convertir un système pour que ses valeurs deviennent celles du centre d'inertie commun. Alors il pourra calculer plus simplement le processus selon les lois de Newton refondues, mais il devra finalement reconvertir ce système selon son propre référentiel. S'il était ainsi transposé dans le référentiel du centre d'inertie commun, le système montré plus haut ressemblerait plutôt à ceci : |

Ce choc frontal implique deux boules de billard qui se déplacent en sens contraire à la vitesse de 0,866 c.
Le champ électrostatique freine d'abord les deux boules avant de les propulser en sens inverse.
Pourtant, il n'immobilise que la moitié de la masse initiale de chaque boule, comme le montre cette image :

La masse totale M de chaque boule a diminué de 2 à 1 kg.
La différence d'énergie delta = 4 – 2 = 2 c 2 joules est stockée dans le champ électrostatique.
Ce sont ces 2 kilogrammes d'énergie cinétique qui vont ensuite propulser chaque boule à la vitesse de 0,866 c.
Le champ de force se comporte comme un ressort parfait, qui agit avec une force égale dans les deux sens.
Très clairement, le champ de force contient de l'énergie potentielle et il possède une masse : c'est de la matière.
|
Au moment où la distance est au minimum, le champ de force contient toute l'énergie nécessaire pour propulser les deux corps à la même vitesse qu'ils avaient à l'origine, mais dans l'autre sens. Cette énergie correspond à la somme de la masse acquise des deux corps (selon Lorentz) au début du processus, puis elle est distribuée à parts égales entre les deux corps. Le centre d'inertie commun constitue un référentiel privilégié. Il permet de contourner la Relativité en évitant la contradiction habituelle que constateraient des observateurs postés dans le référentiel des deux solides. Mieux encore, parce que les effets des transformations de Lorentz sont déjà présents avant le choc, ils se reproduiront de manière parfaitement symétrique après le choc. On pourrait tout aussi bien présumer que les deux boules de billard sont plutôt des électrons. Le processus se déroulerait de la même manière, mais en tenant compte de leur masse beaucoup plus faible. Il n'est pas obligatoire que la masse des deux corps soit la même, ni que leur trajectoire se situe précisément sur le même axe. Toute action qui s'exerce par le travers provoque une simple déviation de la trajectoire selon une hyperbole, ou encore une orbite elliptique s'il y a attraction et si la vitesse est inférieure à la vitesse de libération. Cela conduit au « miroir temporel ». Le miroir temporel. Un choc élastique ou une action à distance observés dans le référentiel privilégié se déroule de la manière la plus simple qui soit. On constate que le trajet des solides après le choc sera strictement le même que celui qui a eu lieu avant lui, comme s'il était reproduit dans un miroir en inversant le sens des trajets. Ce miroir temporel permet de « prévoir l'avenir » en reproduisant le passé :
Le miroir temporel. Cet énoncé est une application du principe de double action. Étonnamment, il résiste à la Relativité et aux transformations de Lorentz.
Cet énoncé indique que toute interaction peut se résumer à une inversion pure et simple du mouvement de part et d'autre d'un plan de symétrie. Ce miroir temporel permet entre autres de prévoir que le périhélie d'une planète devrait demeurer éternellement sur le même plan de symétrie, mais c'est à la condition que cette planète ne subisse aucune autre influence. Cela nous amène à examiner le déplacement du périhélie de Mercure. Une nouvelle explication au déplacement du périhélie de Mercure. En particulier, la première loi de Newton modifiée indique que le référentiel du centre d'inertie commun à l'ensemble du système solaire constitue un référentiel privilégié. En effet, à la condition de négliger l'influence du reste de la Voie Lactée et même des galaxies environnantes, ce point demeure stable. Ce n'est pas le cas du Soleil, qui subit une influence non négligeable de Jupiter et de Saturne en particulier, surtout si ces deux planètes sont en conjonction (vues du Soleil, bien évidemment). De plus, parce que la vitesse relative de chacun des corps est faible devant celle de la lumière, on peut considérer que les transformations de Lorentz sont négligeables. Il est clair qu'à cause de sa masse énorme mais aussi principalement à cause de sa distance considérable, la planète Jupiter déporte le centre d'inertie qu'elle partage avec le Soleil très loin du centre de celui-ci. En effet, le calcul qui en rend compte correspond au principe du levier. Du point de vue de Mercure, le Soleil semblera effectuer une rotation significative autour de ce centre d'inertie commun. Il en ressort que la position, la vitesse et la direction de Mercure doivent être évaluées comparativement au centre d'inertie commun du système solaire. C'est essentiel pour que la force de gravité soit égale dans les deux sens selon le principe de double action. La formule de Newton n'est exacte que si cette condition est respectée. Au lieu de ne considérer que l'influence des autres planètes, il devient crucial de tenir compte aussi de l'orbite du Soleil lui-même autour du centre d'inertie commun à tout le système solaire. Cette orbite est largement influencée par Jupiter et Saturne, qui agissent donc indirectement sur Mercure par le biais du Soleil, mais aussi directement sur lui. Je crois pouvoir dire que cette méthode de calcul devrait aboutir à des résultats plus précis que celle adoptée au XIXe siècle par Le Verrier. Le calcul tensoriel établi par Einstein visait précisément à corriger un résidu inexpliqué de seulement 43" d'arc par siècle. Si donc cette méthode devait donner des résultats plus justes, on ne voit pas bien pourquoi il faudrait continuer de recourir au calcul tensoriel, puisque ce dernier n'explique rien du tout. On a aussi fait grand cas de la vitesse de transmission de la force de gravité, qui était instantanée selon certains, ou qui devait se transmettre à la vitesse de la lumière selon d'autres. Mais si cette force est causée par des champs de force, qui sont situés entre les deux corps, la vitesse de transmission n'a plus d'importance. Si les effets ne sont pas instantanés, ils sont en tous cas simultanés. Cela annule tout risque que deux corps dont la masse est très différente, ici le Soleil et Mercure, ne voient leurs actions réciproques sensiblement déséquilibrées. La loi de l'addition des vitesses de Poincaré. On connaît maintenant la valeur des forces en jeu, mais on a vu qu'il faut considérer que c'est le champ électrostatique qui exerce une pression de radiation sur les deux boules de billard. Aux fins de calculer la pression qu'il exercera, il faut considérer les ondes stationnaires qu'il contient. Pour une partie, ces ondes proviennent de l'électron dit actif, dont l'énergie vaut 3,732 fois celle d'un électron au repos. L'autre partie provient des ondes des électrons de la boule au repos, dont l'énergie est celle d'un électron au repos, c'est à dire inchangée à 1. Ces ondes se déplacent en sens opposé et le rapport R de leur fréquence vaut 3,732 / 1 = 3,732. Puisque leur fréquence n'est pas la même, ces ondes forment à leur tour des ondes stationnaires dites mobiles dont les ventres et les nœuds se déplacent à la vitesse suivante : R = Fa / F = 3,732 bêta = (R – 1) / (R + 1) = 0,577 Le transfert de l'énergie se fera également à cette vitesse, soit 57,7% de la vitesse de la lumière, ce qui explique qu'il en subsiste constamment une partie qui est temporairement stockée dans le champ électrostatique. Du point de vue de l'observateur posté dans le repère du champ, chacune des deux boules de billard semblera se rapprocher puis s'éloigner à la même vitesse, comme l'une des animations l'avait montré plus haut. De plus la vitesse initiale de chaque boule semblera être de 0,577 c et non pas la moitié de 0,866 c, soit 433 c. Pourtant la vitesse relative des deux boules est bien de 0,866 c. On constate que c'est la loi de l'addition des vitesses de Poincaré qui s'applique : bêta1 = bêta2 = 0,577 bêta' = (bêta1 + bêta2) / (1 + bêta1 * bêta2) bêta' = (0,577 + 0,577) / (1 + 0,577 * 0,577) = 0,866 En effet, du point de vue réciproque de l'observateur situé dans le repère du champ électrostatique et de l'un ou l'autre des deux autres postés dans le repère des deux boules de billard, leur vitesse relative vaut bien 0,577 c. Cela semble indiquer que la vitesse relative des deux boules de billard vaut le double, soit 1,1447 c, mais cette symétrie observée du point de vue du champ n'est qu'une illusion. Elle ne se produit réellement qu'au plus fort du choc, au moment précis où les trois observateurs se déplacent à la même vitesse. Les observateurs postés dans le repère des deux boules se considèrent au repos et il est donc hors de question qu'ils voient l'autre boule s'éloigner ou se rapprocher à une vitesse supérieure à celle de la lumière. Ils évalueront cette vitesse à 0,866 c, ce qui est d'ailleurs exact puisque leur perception est la même et que l'un d'eux voit les choses correctement puisqu'il est au repos dans l'éther. En effet, selon la Relativité de Lorentz, seul un observateur au repos, et donc posté dans le repère de la boule de billard qui est au repos, perçoit à coup sûr la vitesse correcte (0,577 c) de l'observateur posté dans le repère du champ électrostatique, et aussi la vitesse correcte de la boule mobile (0,866 c). En principe, le calcul exact devrait être effectué selon ce point de vue, qui est le point de vue absolu. Le problème, c'est qu'il est impossible de repérer le repos absolu. Pour contourner ce problème, je propose donc de considérer le point de vue de l'observateur posté dans le repère du champ électrostatique, qui devient donc un repère privilégié. Cet observateur verra la boule au repos s'approcher à la vitesse correcte, soit 0,577 c. Mais il fera erreur en toute connaissance de cause sur la vitesse de la boule mobile parce qu'il ne calculera pas correctement le ralentissement réel de la fréquence de ses électrons comparativement à l'effet Doppler relatif qu'il constatera. Selon lui, la vitesse des deux boules sera strictement la même, soit 0,577 c. Puisqu'elles se déplacent en sens contraire, il évaluera la vitesse relative des deux boules à 1,1547 c, alors que la formule de Poincaré indique que cette vitesse relative est bel et bien de 0,866 c. La formule de Poincaré s'avère exacte. Il faut souligner qu'elle est basée sur l'effet Doppler relativiste, car elle fait intervenir aussi le ralentissement de la fréquence des électrons, dont nous avons effectivement tenu compte pour évaluer le rapport R des longueurs d'ondes ou des fréquences : R = g / ( 1 – bêta) / 1 = 3,732 bêta1 = bêta2 = (R – 1) / (R + 1) = 0,577 c bêta' = (bêta1 + bêta2) / (1 + bêta1* bêta2) = 0,866 c Les ondes stationnaires du champ électrostatique se déplacent donc au début du choc à la vitesse de 0,577 c alors qu'on aurait pu s'attendre à ce que cette vitesse, qui semble la vitesse moyenne, soit de 0,866 / 2 = 0,433 c. Ce qu'il y a de remarquable, c'est que cette symétrie apparente permet d'élaborer une dynamique conforme à celle de Newton, et qu'il demeure possible de transposer les résultats tels qu'ils seront observés dans tout autre repère. Cette dynamique a l'avantage d'être remarquablement simple, en plus d'être déjà adoptée par toute la communauté scientifique. Au contraire, la mécanique ondulatoire envisagée d'un point de vue absolu s'avère relativement complexe. C'est un peu comme se servir d'un ordinateur : il est bon de savoir comment il fonctionne, mais ce n'est pas vraiment nécessaire. La mécanique de Newton demeure exacte. Finalement, il s'avère beaucoup plus facile pour un observateur d'évaluer les effets de la collision s'il est posté dans le repère du champ électrostatique. C'est qu'en raison de la symétrie, qui n'est pourtant qu'apparente, la mécanique de Newton s'avère tout à fait correcte. La seule correction qu'il faut leur appliquer concerne les transformations de Lorentz que subissent les autres corps, même si ces transformations ne sont qu'apparentes. Il faut souligner que la Relativité d'Einstein était impuissante à analyser correctement plus de deux repères : or il y en a trois ici. À cause de sa réciprocité mal comprise, elle conduit forcément à des résultats contradictoires. Au contraire, la Relativité de Lorentz montre que tout observateur qui se déplace est victime d'une illusion. Elle peut néanmoins prévoir ce qu'il observera, et expliquer d'où vient la contradiction apparente. Cela nous conduit à la loi de la Relativité et à la loi de l'invariance des phénomènes physiques, qui sont toutes les deux des découvertes de Henri Poincaré : |
De son point de vue tout corps matériel semble au repos et tout autre corps ne semble agir, réagir et se soumettre aux transformations de Lorentz que selon sa vitesse apparente. |
La loi de la Relativité des apparences, d'après le postulat de Relativité de Henri Poincaré (1904).
|
Les lois des phénomènes physiques sont les mêmes pour un observateur fixe et pour un observateur entraîné dans un mouvement de translation uniforme, de sorte que nous n'avons et ne pouvons avoir aucun moyen de discerner si nous sommes, oui ou non, emportés dans un pareil mouvement. |
La loi de l'Invariance des phénomènes physiques, de Henri Poincaré (1904).
Les lois des phénomènes physiques, ce sont les lois de Newton à peine retouchées.
|
Bien évidemment, seul celui qui est véritablement au repos voit les choses correctement, mais puisqu'il est impossible de le déterminer, il faut faire avec la Relativité. Nous n'avons pas le choix : il faut considérer que chaque corps matériel dont la vitesse diffère possède son propre repère, même si nous sommes parfaitement conscients qu'il ne peut exister qu'un référentiel cartésien au repos dans l'éther. Il vaut beaucoup mieux avouer qu'on est victime d'une illusion que de se fier à la Relativité d'Einstein, qui aboutit à des « paradoxes » qui ne sont en réalité que des contradictions inexplicables et inacceptables. D'un point de vue absolu, tout est bien différent. Parce que l'éther existe, l'action et la réaction ne sont pas égales et elles dépendent strictement de l'effet Doppler, comme ce diagramme le montre clairement : |
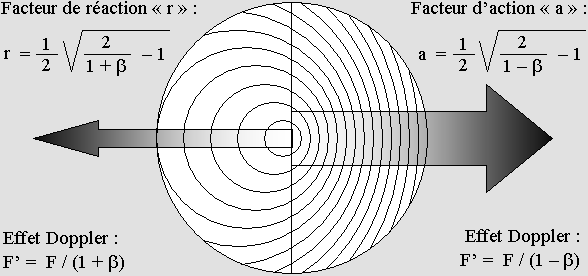
La masse active et réactive.
Ici, l'électron se déplace à la moitié de la vitesse de la lumière.
LA TRANSPOSITION DES REPÈRES
|
On a vu que dans un premier temps, il vaut mieux considérer le repère du champ de force dans le but de pouvoir y appliquer les lois de Newton. Il demeure cependant possible d'évaluer quelle sera la perception qu'on aura de ce phénomène s'il était observé à partir d'un autre repère. À n'en pas douter, mon scanner du temps permet de généraliser les transformations de Lorentz, car il peut transposer les valeurs entre deux repères dont la vitesse n'est pas la même, mais qui sont tous les deux en mouvement. Les équations de Lorentz n'effectuent la transposition que d'un repère en mouvement à un autre qui est au repos (et non le contraire comme on le croit généralement). Les équations réversibles de Poincaré permettent de faire l'un et l'autre, mais là aussi elles sont impuissantes à traiter un changement de repère si tous les deux sont mobiles. On peut cependant y arriver en deux étapes à l'aide de la formule de l'addition des vitesses, qui est aussi de Poincaré. Mieux encore, ce scanner peut traiter simultanément de nombreux repères différemment transformés, et même ceux dont la direction ne correspond pas à l'axe des abscisses. Par exemple, il peut reproduire quel aspect aurait une roue dentée qui tourne si elle est actionnée par quatre « crémaillères » sur quatre côtés, et dont les unités sont cylindriques : |

Le scanner du temps peut transposer tout un système d'un repère à l'autre.
La vitesse de l'engrenage supérieur passe de 0,866 c à 0,9897 c avec contraction de 0,5 à 0,1428.
Même les engrenages opérant dans les directions transversales sont traités correctement.
Ces résultats sont conformes à la Relativité de Lorentz et à la loi de l'addition des vitesses de Poincaré.
|
Dans l'image de gauche, le centre de la roue est au repos dans l'éther. Le point de contact des engrenages (indiqué par le trait noir inférieur) se déplace à la vitesse de 0,866 c et l'extrémité des dents de la roue frôle de justesse la vitesse de la lumière. À droite, le « scanner du temps » montre cette roue telle qu'elle serait observée à partir d'un repère qui se déplacerait vers la gauche à la vitesse de 0,866 c, ce qui fait que la crémaillère inférieure y semble au repos (ses cylindres ne sont pas contractés) alors que ce n'est pas le cas dans les faits. On constate en particulier que la vitesse de la crémaillère supérieure passe de 0,866 c à 0,9897 c. Pourtant, sa vitesse absolue comparativement à l'observateur vaut deux fois 0,866 c et donc 1,732 c. L'observateur est donc victime d'une illusion et il voit cette crémaillère se déplacer à une vitesse inférieure à celle de la lumière. On peut même observer que le scanner arrive à dilater certains objets et à en contracter d'autres dans la même opération. Il respecte en tous points la Relativité de Lorentz et non pas les faits absolus, ce qui est absolument stupéfiant. Et tout ceci se fait conformément à la loi de l'addition des vitesses. Voilà donc une autre trouvaille de Poincaré (là aussi il fut copié joyeusement par Einstein) qui s'avère d'une importance capitale. |
| 01 | 02 | 03 | 04 | 05 | 06 | 07 | 08 | 09 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 17 | 18 | Vous êtes ici. | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 |
Gabriel LaFrenière, Bois-des-Filion en Québec. Sur l'Internet depuis septembre 2002. Dernière mise à jour le 12 septembre 2009. Courrier électronique : veuillez consulter cet avis. La matière est faite d'ondes, © Gabriel Lafrenière, juin 2002. |