LA TACHE D'AIRY
...et l'ellipsoïde d'Airy.
|
|
La tache d'Airy. À gauche, le relief est artificiel mais très révélateur.
Afin de mieux montrer les anneaux, ces diagrammes indiquent l'amplitude et non l'énergie, qui vaut son carré.
|
|
Voici une vue longitudinale des environs du plan focal, illuminé selon un angle d'ouverture sur l'axe de 30°.
Sauf erreur, personne n'était encore parvenu à réaliser une animation semblable.
|
|
Voici un diagramme composite, toujours pour un angle de 30° sur l'axe (60° bilatéral).
Au lieu d'être représentées en gris moyen, les zones où l'énergie est plus faible ont été assombries.
![]()
![]() absolu2000@hotmail.com Page d'accueil : La matière est faite
d'ondes.
absolu2000@hotmail.com Page d'accueil : La matière est faite
d'ondes.
|
Le 17 Juin 2011. Voici une vidéo qui montre d'une manière éclatante que notre médium virtuel en trois dimensions est maintenant au point. 11-06_3D_Airy_Disk.mkvComme je l'ai indiqué, il s'agit d'une première. Pour autant que je sache, personne n'était encore parvenu à reproduire expérimentalement la tache d'Airy, qui est certainement le phénomène optique le plus remarquable. Vous pouvez examiner et compiler vous-même le programme (en langage C) que j'ai écrit à cet effet : |
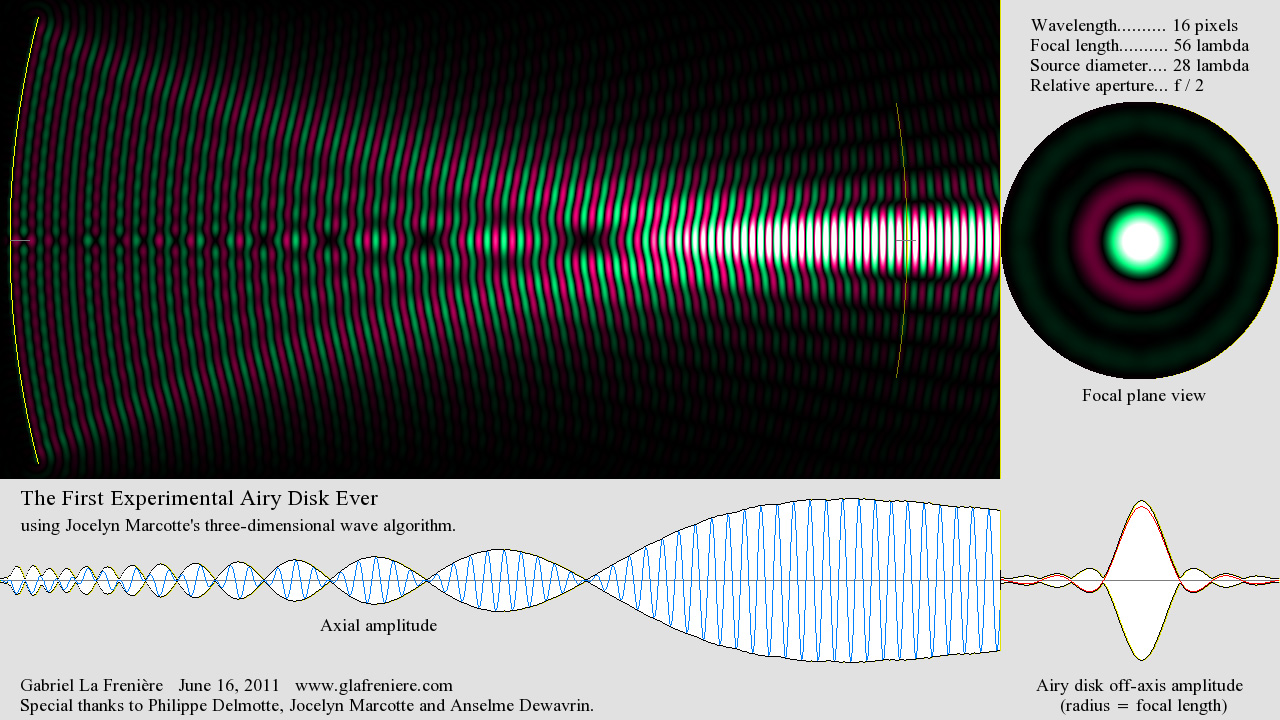
|
M. Jocelyn Marcotte a mis au point un algorithme à trois dimensions dont l'ingénierie est absolument parfaite et garantit une propagation uniforme dans toutes les directions avec une précision stupéfiante. Vous comprendrez néanmoins que votre ordinateur mettra beaucoup de temps à produire une image, car il lui faudra effectuer des milliards et des milliards de calculs. Il doit en effet composer avec un espace à trois dimensions (1000 x 480 x 480) contenant plus de 230 millions de cellules individuelles de la taille d'un pixel et entourées chacune de 26 voisines dont il faut évaluer l'influence relative. Si des amateurs comme moi arrivent à faire mieux que les professionnels, c'est la preuve que rien ne va plus de nos jours dans le monde de la physique... Comme je l'ai écrit ci-dessous, les opticiens et les acousticiens en général manquent sérieusement de vision et d'envergure. Je ne comprends vraiment pas ce qui les incite à ignorer ce laboratoire de l'avenir. Le mépris qu'ils manifestent pour ce que nous faisons ne les honore guère, mais c'est surtout leur inconscience qui étonne. Parce qu'ils ne disposent d'aucun outil moderne et efficace, ils ne sont même pas en mesure de vérifier par eux-mêmes le bien-fondé de mes hypothèses, particulièrement en ce qui concerne l'optique du mouvement, c'est à dire la Relativité. D'ailleurs, grâce à ce nouvel outil désormais tout à fait fonctionnel, je serai en mesure de vous présenter en images saisissantes tout ce qu'il faut savoir sur la Relativité. Et ce sera sans toutes ces balivernes à propos d'une prétendue "transformation de l'espace-temps"... Croyez-moi, ça n'est pas si compliqué que ça en a l'air. C'est dans la simplicité qu'on comprend le mieux. Il suffit de bien explorer le sujet au préalable, avec toute la rigueur nécessaire. Descartes ne disait-il pas que toute vérité devient alors fondamentalement évidente? |
|
Un ancien programme. Je suis quand même très fier d'avoir réussi à mettre au point moi-même un algorithme capable de calculer l'ensemble de l'ellipsoïde d'Airy à une vitesse bien plus grande qu'avec mes précédents programmes. Le programme était disponible sous le nom de Ether16.bas dans ma suite sur l'éther, que vous pouvez télécharger en cliquant sur les liens suivants : http://www.glafreniere.com/programmes/Ether16.exe http://www.glafreniere.com/programmes/Ether16.bas Le diagramme complet de toute la région du plan focal sera achevé en quelques secondes. Vous pourrez alors déplacer le curseur avec la souris pour obtenir instantanément l'aspect de la tache d'Airy pour différentes distances du plan focal. Ce programme montre clairement que cette fameuse "tache" n'a pas seulement un diamètre, mais aussi une longueur qui vaut sensiblement le double du carré de ce diamètre. Mais les formules du programme montrent que ce n'est pas tout à fait exact, comme on le verra plus loin. De plus, les phases varient d'une manière vraiment surprenante le long de l'axe, et j'ai d'ailleurs retrouvé un phénomène identique dans le rayonnement du champ de force électrostatique. C'est sans doute ce phénomène qui explique l'effet de répulsion ou d'attraction entre électrons et (ou) positrons. Les photons n'existent pas. Les électrons rayonnent continuellement des ondes en utilisant l'énergie des ondes qui circulent dans l'éther et qui les traversent. Ces ondes ne sont pas perceptibles normalement, mais elles le deviennent si les électrons sont déséquilibrés. D'autre part on sait que les électrons sont présents dans un atome par paires, un de chaque spin, conformément au principe d'exclusion de Pauli. La page sur la lumière montre que les électrons réagissent différemment à un rayonnement selon leur spin. Ils émettent aussi leurs ondes selon un diagramme de rayonnement très particulier qui présente des zones alternativement en phase et en opposition de phase, ces zones oscillant en rotation ou sur un seul plan. C'est ce qui explique que la lumière peut être polarisée, mais pas nécessairement. Et enfin, les électrons vibrent tous selon une fréquence et une amplitude constantes, ce qui permet d'expliquer la constante de Planck. Au contraire la fréquence de la lumière est beaucoup plus basse et elle dépend des oscillations des électrons, qui se comportent un peu comme des pendules oscillant faiblement ou décrivant de petits cercles autour de la position qui leur est assignée dans l'atome. Un pendule étant synchrone, la lumière émise par un électron positionné sur une couche atomique donnée possède une fréquence invariable qui justifie les raies spectrales. Contrairement au son qui se propage dans l'air, les ondes de la lumière ont donc une structure composite relativement complexe. Disons-le clairement : les photons n'existent pas. Cette affirmation risque de vous choquer, mais sachez que ces pages en font la preuve. La tache d'Airy est un phénomène ondulatoire. Ici, il sera tout simplement question de la tache d'Airy, et bien sûr cette figure de diffraction sera traitée en postulant qu'il s'agit purement et simplement d'un phénomène ondulatoire. D'ailleurs personne n'y a jamais vu la moindre trace d'un photon. Voici comment on peut représenter l'intensité de la lumière à l'intérieur du disque central et de ses trois premiers anneaux : |
|
L'amplitude. |
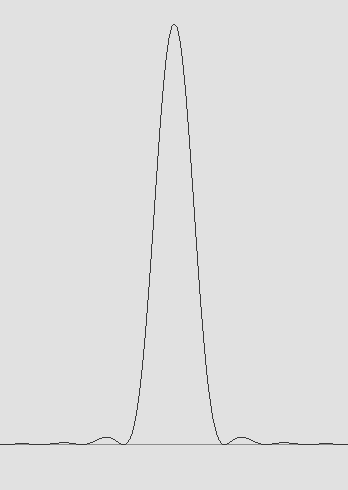
L'énergie. |
|
Le diagramme supérieur gauche montre que le premier anneau est en opposition de phase sur le disque central, comme d'ailleurs tous ceux de rang impair. Celui du dessous ne tient pas compte de la période. C'est l'astronome sir George Biddell Airy qui a réussi le premier à calculer le diamètre exact de ce disque, là où se situe le premier zéro d'amplitude. On parlera donc dans ces pages du chiffre d'Airy, qui vaut 2,44 ou encore 1,22 en termes de rayon. Le diagramme de droite montre l'énergie, c'est à dire la luminosité relative des différentes zones de la tache d'Airy jusqu'au troisième anneau. Il y en a beaucoup d'autres. Cette énergie est évidemment toujours positive, car selon une loi énoncée par Augustin Fresnel elle vaut le carré de l'amplitude. La lumière y est répartie de manière décroissante. Le disque central : 83,778 %; le premier anneau : 7,215 %; le deuxième : 2,77 %, etc. Le diamètre du disque central dépend de l'angle d'ouverture d'un faisceau de rayons lumineux. Il dépend donc de la focale F comparée au diamètre D de l'ouverture lumineuse, qui doit être uniformément éclairée. Il dépend aussi de la longueur d'onde (lambda) , celle de la couleur la plus visible (le vert lime) valant 0,00055 mm. On a :Diamètre du disque central de la tache d'Airy : 2,44 * lambda * F / DPar exemple, un objectif ƒ/8 dont le diamètre D vaut 100 mm et dont la focale F vaut 800 mm produit un disque central de 0,01 mm environ pour le vert. Le rayon angulaire dépend de la longueur d'onde et du diamètre D. Peu d'auteurs mentionnent que ce phénomène s'applique à toutes les ondes sans exceptions, y compris le son. Conformément au principe de Huygens, on peut donc produire une "tache d'Airy sonore" au centre de courbure d'une calotte sphérique sur laquelle on a réparti uniformément de petits haut-parleurs. Une centaine devrait suffire. Rayon angulaire de la tache d'Airy en radians : 1,22 * lambda / D Cette formule est inexacte. Le diamètre du disque central, d'un point d'amplitude nulle à l'autre, vaut exactement une longueur d'onde si la source est un hémisphère complet, ce qui montre bien que la formule de sir Airy devient vite inexacte si l'angle d'ouverture est considérable. De plus, dans ce cas, il s'agit plus exactement d'une sphère et non d'un disque. Il faut donc chercher une formule qui soit capable de concilier tous les angles. Il suffit d'examiner attentivement l'animation montrée en début de page pour constater que l'angle d'ouverture y transparaît nettement, particulièrement aux environs du plan focal, là où se forment les anneaux. Cet angle d'ouverture « fantôme » détermine donc au moins approximativement le diamètre de ce disque. L'angle d'ouverture (thêta) est l'angle du faisceau conique lumineux (la caustique) rapporté à l'axe central, et il s'agit donc du demi-angle comparativement à celui du cône lumineux dans son entier. On considérera dans cette page que la longueur d'onde (lambda) vaut 0,00055 mm, soit celle de la lumière la plus visible (vert lime). Ne serait-ce que d'un point de vue strictement géométrique, on présume ainsi que le diamètre du disque central de la tache d'Airy devrait valoir : D = lambda / sin(thêta) Or c'est effectivement la mesure de la tache asymétrique produite par une ouverture carrée. C'est aussi la largeur de la bande produite par une fente lumineuse de largeur D. Toutefois sir Airy a montré qu'il faut appliquer un terme correcteur dans le cas d'une ouverture circulaire. De plus on verra plus loin qu'on peut avantageusement utiliser l'angle thêta de manière à éviter le piège du diamètre comparé à la focale, qu'on appelle "l'ouverture relative" en optique : D = 1,22 * lambda / sin(thêta) Par exemple, une ouverture relative de ƒ / 8 correspond à : q = arc tan(0,5 / 8) = 3,576° et la formule donne un disque de 0,01 mm comme on l'a vu plus haut.Une formule plus précise. Toutefois on remarque que la constante 1,22 de sir Airy n'est plus conforme aux résultats expérimentaux ni au calcul selon le principe de Huygens si l'angle d'ouverture devient important. Il faut alors appliquer un deuxième terme correcteur de manière à neutraliser peu à peu la différence entre 1,22 et 1. Si vous avez téléchargé mon programme Ether16.bas, vous constaterez que les formules utilisées dans le code source fonctionnent correctement pour tous les angles d'ouverture jusqu'à 180°: Diamètre de la tache centrale : D = lambda * 1,22 / sin(thêta) – 0,22 (1 – cos(thêta))Grand rayon de l'ellipsoïde : R = 2 * lambda * (1 / sin(thêta)) ^ 2 – lambda * sin(thêta)Par exemple, un angle d'ouverture de 10° (soit ƒ/ 2,8) conduit à une tache dont le diamètre vaut 6,8 fois la longueur d'onde, et le grand rayon de l'ellipsoïde vaut 66 fois la longueur d'onde. En lumière verte, une telle ouverture exige donc une précision de 0,036 mm pour une mise au point parfaite. Il en ressort aussi que pour une ouverture relative de ƒ/ 0,1 ou moins, le diamètre de la tache d'Airy fait exactement une longueur d'onde. De plus, mon programme montre clairement que pour une source émettrice sphérique complète, on obtient une tache d'Airy tout à fait particulière : l'équivalent d'un électron ! La tache d'Airy à très grande ouverture. Voici un tableau comparatif. Il s'agit de vérifier que la formule corrigée permet d'obtenir une plus grande précision si l'angle est très ouvert. Le diamètre du disque central est donné en longueurs d'onde, et il faudrait donc le multiplier par la longueur d'onde 0,00055 pour l'obtenir en millimètres : |
| thêta | Ouverture ƒ | Selon l'ordinateur | 1,22 / sin(thêta) | 1,22 / sin(thêta) – 0,22 (1 – cos(thêta)) | Constante |
| 10° | ƒ / 2,836 | 7,0092 | 7,026 | 7,011 | 1,217 |
| 15° | ƒ / 1,866 | 4,6904 | 4,714 | 4,706 | 1,214 |
| 20° | ƒ / 1,374 | 3,5364 | 3,567 | 3,554 | 1,21 |
| 30° | ƒ / 0,866 | 2,3935 | 2,44 | 2,411 | 1,197 |
| 45° | ƒ / 0,5 | 1,6514 | 1,725 | 1,661 | 1,168 |
| 60° | ƒ / 0,289 | 1,3004 | 1,409 | 1,299 | 1,126 |
| 90° | ƒ / 0 | 1 | 1,22 | 1 | 1 |
Le chiffre 1,22 de sir Airy est inexact à grande ouverture.
|
Le programme qui a produit les diagrammes montrés dans cette page utilise le principe de Huygens. Les résultats compilés ci-dessus selon l'ordinateur sont précis à trois décimales près, du moins si l'on en juge par celui que l'ordinateur a calculé (on prévoyait évidemment une longueur d'onde exactement) dans le cas d'un demi-angle de 90°. On note qu'ils ne correspondent pas tout à fait à ceux prévus par la formule suggérée, mais la différence est minime. Il faut donc retenir que si l'angle est très ouvert, la constante 1,22 de sir Airy se rapproche de l'unité. Elle n'est donc pas vraiment constante. Le contraste d'un objectif très ouvert est mauvais. Ci-dessous, on a superposé deux courbes montrant l'énergie de la tache d'Airy pour des ouvertures de ƒ/0,0001 (en rouge) et de ƒ/2,8 (en vert). Elles ont été calibrées de manière à ce que le premier zéro d'énergie coïncide de manière à mieux comparer l'énergie relative des anneaux. On constate que l'amplitude des anneaux éloignés devient vite négligeable si l'ouverture relative est élevée (ƒ/2,8 ou plus). Toutefois, si l'angle du faisceau lumineux est très grand, l'amplitude des anneaux devient significative. En fait, elle tend à respecter la règle du carré de la distance, de sorte que la luminosité totale de chaque anneau tend à devenir égale à celle du disque central. |
|
|
En rouge : ƒ / 0,0001. En vert : ƒ / 2,8
Le contraste d'une image diminue radicalement si l'angle d'ouverture est très grand.
|
|
Une ouverture relative de ƒ/ 1 (en rouge) est acceptable.
|
Ci-dessus, on a juxtaposé les lobes de la tache d'Airy selon ƒ/ 1 ou 26,6° (en rouge) comparés à ceux de la tache présumée idéale à ƒ/ 28 ou 1°, représentés en vert. On remarque une légère détérioration d'environ 10% en énergie, ce qui est déjà significatif. Cette détérioration augmente de manière exponentielle par la suite, ce qui permet d'en conclure que le contraste d'une image obtenue avec une lentille très lumineuse ƒ / 0,7 ou 0,5 est très mauvais. Le disque central mesure alors moins de 0,001 mm alors que le film ne pouvait enregistrer autrefois que 0,025 mm. Jusqu'à récemment, ce problème ne se posait donc pas. Toutefois les caméras électroniques atteindront sans doute bientôt une telle précision, et alors il faudra refaire les tests en ce sens. Très clairement, il faudra éviter d'utiliser des lentilles trop lumineuses et des pixels trop petits. D'ailleurs on montre ci-dessous que la figure de diffraction complète de la tache d'Airy a une longueur, et que celle-ci approche de la longueur d'onde à grande ouverture, ce qui rend la mise au point exacte pratiquement impossible. On en conclut que la limite minimum d'un pixel en lumière visible se situe aux environs de 0,002 mm. Même s'il était possible un jour d'être plus précis, ce ne serait pas souhaitable. D'ailleurs, toute ouverture relative inférieure à ƒ/2 devient problématique pour bien d'autres raisons.Un diagramme longitudinal. On a vu plus haut que selon l'ordinateur le diamètre du disque central vaut une longueur d'onde exactement si l'angle d'ouverture correspond à une demi-sphère. C'est d'ailleurs en utilisant le même algorithme que l'ordinateur a produit le diagramme longitudinal suivant : |
|
|
Vue longitudinale de l'ellipsoïde d'Airy selon un angle d'ouverture de 90° ou ƒ/ 0,0001.
|
Il faut comparer ce diagramme avec ceux qui ont été montrés au début de cette page, et dont l'angle était de 30°. Puisque ici l'angle d'ouverture total vaut 90°, chacun des anneaux contient exactement la même quantité d'énergie. Le disque n'est pas encore sphérique, ce point n'étant atteint que pour une illumination sphérique intégrale (360°). Parce qu'on a 1 * lambda seulement et non pas 1,22 * lambda / D, la luminosité du disque central est ici plus intense toutes proportions gardées.Cette situation est intéressante, car on peut observer que la vitesse de l'onde centrale au moment où elle traverse le centre de courbure atteint deux fois la vitesse normale des ondes. Il en résulte une inversion de phase qui permet d'expliquer pourquoi le noyau central de l'électron vaut une onde entière, et non pas la demi-onde classique des ondes stationnaires. Si l'on passe de l'hémisphère à la sphère complète, on obtient plutôt des ondes stationnaires parfaitement sphériques et concentriques. Comme on le verra plus loin, le diagramme est alors le même que celui d'un électron au repos, donc avec symétrie radiale tous azimuts. L'ordinateur fonctionnant à 1,7 GHz avait mis deux heures pour produire chacune des 20 images qui composent l'animation montrée ci-dessus. Il s'agissait d'additionner des milliers d'ondelettes de Huygens comme c'est le cas pour établir la courbe habituelle de la tache d'Airy. Toutefois, la symétrie radiale étant brisée dans le cas d'une vue longitudinale, il fallait refaire le calcul pixel par pixel. Toutefois, mon nouveau programme Ether16 ne met que quelques secondes pour achever le même diagramme car il fait la sommation de courbes et non de points. Le « cigare d'Airy ». L'ordinateur peut aussi montrer les variations longitudinales de l'amplitude selon différents angles d'ouvertures, entre 180° et 15°. Noter que 180° rapportés à l'axe correspond à une illumination sur une sphère complète . La tache d'Airy, dans son espace réel en trois dimensions, affecte en réalité la forme d'un cigare. C'est plus exactement un ellipsoïde de révolution allongé qui se termine de part et d'autre par une série de zones régulièrement espacées où l'énergie est nulle : |
|
|
Les variations de l'ellipsoïde d'Airy.
On a successivement : 360°, 240°, 180°, 120°, 90°, 60° et 30°.
|
Répétons qu'il s'agit d'une vue longitudinale, qui est rarement, sinon jamais montrée. Le plan comprend l'axe optique. La ligne verticale noire représente le plan focal. Les deux lignes en grisé de part et d'autre de l'axe marquent une longueur d'onde exactement de manière à pouvoir comparer les différents résultats. On observe en premier lieu que si la source rayonnante est la surface interne d'une sphère complète, la tache d'Airy devient plutôt une sphère d'Airy dont le diamètre vaut une longueur d'onde exactement. D'un point de vue strictement ondulatoire, l'électron correspond à ce modèle. L'ellipsoïde d'Airy possède donc une longueur L, et il est facile de l'obtenir à partir du diamètre D du disque central, parce qu'elle correspond sensiblement à l'angle d'ouverture thêta comparé à 180° :L = 180 D / thêta Pour fixer les idées, la longueur de l'ellipsoïde vaut 10 fois sa largeur pour une ouverture relative de ƒ/ 1,4 et 20 fois sa largeur si l'on ferme à ƒ/ 2,8. Il est clair que la tolérance pour une mise au point idéale en photographie correspond à la moitié de cette valeur. La première zone d'amplitude nulle se situe en effet à la moitié de cette distance de part et d'autre du plan focal et le diagramme montre que c'est à coup sûr le pire endroit où situer la surface photosensible. La tolérance pour une ouverture de ƒ/ 2 ou moins en lumière visible lors de la mise au point est donc incroyablement faible. Elle est de l'ordre d'un centième de millimètre. Les caméras électroniques actuelles (vers 2004) n'atteignent pas la précision de la tache d'Airy (0,0026 mm) à cette ouverture, mais ça viendra. Cela donne à penser qu'il vaudra toujours mieux s'en tenir à des ouvertures de ƒ/ 4 et même plus si la précision de l'image est capitale. Même si le diamètre de la tache d'Airy est inconnu, on peut quand même obtenir la longueur L de l'ellipsoïde d'Airy. Rappelons que l'angle thêta est l'angle sur l'axe, donc le demi-angle d'ouverture : Longueur de l'ellipsoïde d'Airy : L = 4 * lambda * (1 / sin(thêta)) ^ 2 – lambda * sin(thêta) L'apodisation. Si l'apodisation vous intéresse, allez à la page sur le sténopé. On y montre que cette méthode permet d'éliminer complètement les anneaux qui entourent le disque central. Elle produit une seule tache lumineuse contenant presque toute la lumière, mais elle est impraticable la plupart du temps. Le problème, c'est que cette tache est plus grande et qu'il faut augmenter le diamètre de l'ouverture pour compenser. Toutefois, il faut éviter les conclusions hâtives. Tout indique en effet que cette méthode serait avantageuse dans le cas des petits objectifs sans obstruction et sans diaphragme à iris. Un remise en question. Dans le contexte de l'optique "délinquante", on peut montrer que certaines idées reçues pourraient être remises en question. C'est le cas par exemple de l'obstruction et de l'apodisation. Le phénomène de l'ombre qui se forme derrière un objet est particulièrement révélateur. Étonnamment, on peut en déduire que la lumière traverse les objets, ce que personne à ce jour ne semble avoir remarqué. Mieux encore, l'électron présente des similitudes étonnantes avec la tache d'Airy, au point qu'on peut l'expliquer parfaitement de cette manière, aussi bien dans sa création que dans sa structure. Un programme d'ordinateur. De plus il existe une méthode, apparemment inconnue, qui permet de calculer ce phénomène sur ordinateur. Puisqu'on fait la sommation des ondelettes de Huygens, on peut considérer qu'il s'agit à toutes fins pratique d'un calcul différentiel, mais sans les tracasseries habituelles comme l'évaluation des conditions aux limites. J'ai tenté à maintes reprises de contacter des opticiens à ce sujet, mais n'étant pas l'un des leurs, ils m'ont toujours traité avec le plus souverain mépris. Pourtant aucun d'eux à ma connaissance n'a réussi à produire des diagrammes et des animations comme celles qui figurent dans cette page. Et si c'était le cas, on peut dire que ces gens savent bien cacher le fruit de leur travail. Il vous suffira de taper "tache d'Airy", "Airy disk" ou "disque d'Airy" dans Google pour vous en convaincre. Sauf erreur les vues longitudinales animées de la tache d'Airy montrées ici constituaient donc une première mondiale. Les ondes sur ordinateur grâce à l'Éther Virtuel. Les premières images obtenues par M. Philippe Delmotte au moyen de « l'Éther Virtuel », dont il est l'inventeur, constituent sans contredit une première mondiale. Et vous n'avez encore rien vu, car ce médium virtuel nous permettra surtout de montrer que la matière est bel et bien faite d'ondes exclusivement, comme je l'ai affirmé dès l'an 2000. D'une manière remarquable, tous les essais tentés jusqu'à maintenant indiquent que le principe de Huygens est exact. Nous n'avons jamais noté la moindre différence entre nos résultats et le calcul effectué à l'aide des ondelettes de Huygens. La deuxième image ci-dessous représente le faisceau d'un laser (ou celui d'un sténopé). Le laser se trouve à gauche et la tache d'Airy en voie de formation se trouve à droite. On trouvera plus de détails à la page sur le sténopé. Ce diagramme n'est pas à l'échelle et devrait être au moins 100 fois plus long. Ainsi les zones sombres sont beaucoup plus allongées : ce sont des « tunnels noirs ». J'ai toutes les raisons de croire que les électrons sont captifs du noyau d'un atome à l'intérieur de tels tunnels. Remarquer les distances, qui suggèrent fortement la série de Balmer et les raies spectrales de l'hydrogène. Les 8 électrons périphériques d'un atome font exception parce que leur emplacement dépend plutôt du rayonnement des protons, qui se fait selon les huit sommets d'un cube. En comparant les deux diagrammes suivants, on pourra constater que la structure du faisceau d'un laser présente des similitudes avec celui d'un télescope : |
|
|
La structure du faisceau lumineux au foyer d'un télescope. On a ici ƒ/ 2, soit arc tan (0,5 / 2) = 14°.
|
|
La structure du faisceau lumineux d'un laser ou d'un sténopé : la diffraction de Fresnel, selon Huygens.
|
|
Une première : le diagramme d'une source linéaire extrêmement mince, dans l'Éther Virtuel de Philippe Delmotte.
Si vous êtes un opticien, prenez garde de rater le train ; ce médium virtuel est désormais incontournable.
Tous vos beaux calculs et vos belles équations ne vous seront plus d'aucune utilité.
Seul un médium réel ou virtuel peut véritablement montrer comment ces phénomènes se produisent.
|
|
À gauche, la diffraction de Fresnel sous les transformations de Lorentz (voir mon Scanner du Temps).
Philippe Delmotte a synchronisé les sources en fonction du temps local découvert par Henri Poincaré.
Autrement, on obtiendrait le sillage classique d'un bateau qui fend l'eau, comme on le montre à droite.
Cela permet d'obtenir des ondes inclinées selon l'angle thêta, et qui demeurent dans l'axe perpendiculaire.
Ainsi, la structure de la diffraction de Fresnel demeure invariante quelle que soit la vitesse de la source.
Voila donc une autre preuve que la Relativité est exacte, mais que c'est celle de Lorentz et de Poincaré.
La suite sur la tache d'Airy à la page suivante.
|
Gabriel LaFrenière, Bois-des-Filion en Québec. Sur l'Internet depuis septembre 2002. Dernière mise à jour le 14 octobre 2009. Page d'accueil : La matière est faite d'ondes. Courrier électronique : veuillez consulter cet avis. La théorie de l'Absolu, © Luc Lafrenière, mai 2000. La matière est faite d'ondes, © Gabriel Lafrenière, juin 2002. Optique des miroirs, © Gabriel Lafrenière, juillet 2001. ISBN 2-9806972-2-2 |