LA NORME À QUATRE COULEURS
Rouge - Jaune - Vert - Bleu
![]()
![]() Page d'accueil : La matière est faite
d'ondes.
Page d'accueil : La matière est faite
d'ondes.
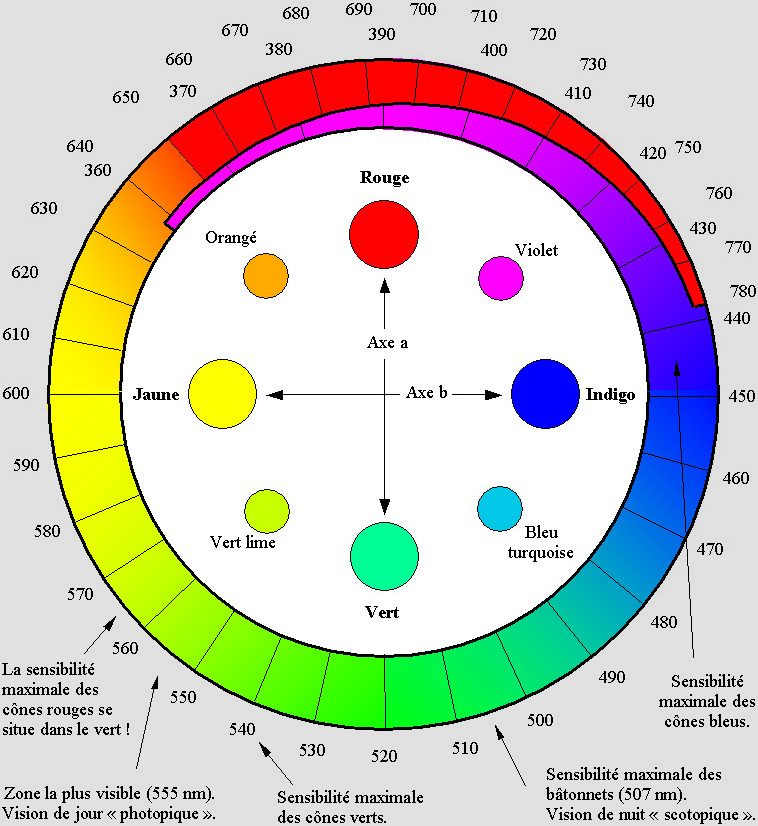
Ce tableau n'est pas exact. Il est très difficile de déterminer une couleur selon la longueur d'onde.
Par exemple, la lumière d'un laser émettant vers 650 nm nous semble rouge parce qu'elle est pure.
Mais normalement, un objet de cette couleur semble orange parce qu'il reflète aussi du jaune.
La couleur complémentaire du jaune normal (environ 585 nm) est l'indigo (environ 440 nm).
|
Mise au point. J'ai écrit ce texte il y a longtemps déjà et je me rends compte que très peu de gens, après l'avoir parcouru, on vraiment saisi la portée de ce que je propose. Je considère qu'on perd beaucoup de temps, d'efforts et d'argent à mettre au point de nouveaux systèmes parce qu'on ne prend pas la peine de bien en maîtriser tous les aspects. Par exemple, on sait que les Romains construisaient des bateaux sans gouvernail. Le point important, c'est qu'à partir du moment où quelqu'un a montré qu'un bateau muni d'un gouvernail était bien plus manœuvrable, et plus facilement, ceux qui ont continué de construire des bateaux sans gouvernail ont vu leur flotte anéantie et ils ont perdu la guerre... En d'autres termes, si les ingénieurs de l'industrie avaient déjà majoritairement adopté ce système, les autres seraient au bord de la faillite. Ce qu'il faut bien comprendre, c'est que le fait d'ajouter une quatrième couleur aux téléviseurs ou aux écrans d'ordinateurs ne complique pas le système. Ça le simplifie au contraire non seulement parce qu'il suffit d'afficher deux couleurs par pixel au lieu de trois, mais encore parce que le code jpeg ou mpeg nécessaire est lui aussi simplifié d'autant. Le principe n'est pourtant pas bien compliqué. Si par exemple on prend la peine d'analyser la longueur d'onde de la lumière réfléchie par un ballon jaune, même si sa couleur est vraiment saturée, on se rend compte qu'il réfléchit aussi du rouge et du vert pour environ la moitié de la luminance. C'est uniquement le bleu qui est absent. Il est donc possible de reproduire ce jaune en faisant appel en plus aux pixels rouges et verts voisins, mais en tenant compte de la luminosité précise de chacun des pixels, donc en respectant scrupuleusement la résolution que l'écran est en mesure d'afficher. Il est clair aussi que les imprimeurs auraient intérêt à adopter ces quatre couleurs, non seulement parce que cela éliminerait les problèmes de compatibilité (rouge, vert et bleu à convertir en jaune, magenta et cyan), mais aussi parce que la saturation des couleurs imprimées serait bien meilleure. Bien sûr, il faudrait utiliser une couleur d'encre additionnelle, mais en faisant remarquer qu'en plus du noir qui demeure obligatoire, un pixel ne réclame jamais plus de deux couleurs. |
LE CERCLE DES COULEURS
|
Notre œil ne voit pas les couleurs selon leurs longueurs d'onde, et donc selon une échelle qui a un début et une fin. Par je ne sais quel miracle, il arrive à « boucler la boucle » en fusionnant le violet dans le rouge. On peut ainsi afficher successivement toutes les couleurs de l'arc-en-ciel du rouge au violet et passer ensuite du violet au rouge sans constater la moindre anomalie. C'est pour cette raison qu'il est possible de reproduire les couleurs selon un cercle. Pourtant, si l'on s'en tient aux longueurs d'onde comme le montre l'illustration ci-dessus, le violet n'a aucun lien avec le rouge. Ce n'est pas un mélange de rouge et de bleu. De plus, dans le spectre, les pourpres (magenta, mauve, fuschia, rose violacé) « brillent » par leur absence car ils n'ont pas de longueur d'onde précise. Autre bizarrerie, on a constaté que notre oeil était en mesure de distinguer toutes les couleurs de l'arc en ciel avec une précision remarquable malgré le fait qu'aucun des trois types de cônes présents sur sa rétine ne soit sensible au rouge ni au violet. On sait aussi que la lumière blanche, qui est celle que le Soleil émet, contient davantage de vert et de jaune que de rouge et de bleu. C'est à cause du rayonnement du « corps noir », qui présente une distribution vaguement en forme de cloche apparentée à la distribution normale dite de Gauss-Laplace. C'est d'autant plus grave que notre oeil perçoit beaucoup moins le bleu que le vert lime (ou le jaune verdâtre), ce qui fait que la couleur bleue est doublement affaiblie. C'est pour cette raison que ce vert lime occupe plus de la moitié de la luminance. Dans le but d'équilibrer les couleurs, plusieurs ont proposé de diviser le vert lime actuel en deux tons distincts : le jaune et le vert émeraude. Ce serait la moindre des choses, car même après leur division, chacune de ces deux couleurs continue d'être plus lumineuse que le bleu. Les couleurs du spectre visible nous apparaissent différentes selon leur longueur d’onde, qui est donnée ci-dessus en nanomètres (550 nm = 0,00055 mm). Le prisme nous les montre dans l’ordre : rouge, orange, jaune, vert, bleu, violet. Ces couleurs - et non pas les nuances intermédiaires - sont universellement reconnues comme telles sans qu’on sache exactement pourquoi (Berlin & Kay, 1969). Les gens y ajoutent le brun et le rose, et considèrent que le noir, le blanc et le gris sont aussi des couleurs. Il y en a onze en tout. Ce sont des couleurs dites « psychophysiques ». Contrairement à ce qu’on laisse croire, il n’existe pas de véritables couleurs primaires ou secondaires. On note aussi que la lumière d'un laser émettant vers 650 nm nous semble rouge, alors que la couleur d'un objet qui reflète majoritairement cette longueur d'onde nous apparaît franchement orange. L'étude des couleurs fait ressortir un grand nombre d'anomalies de ce genre. Le cercle des couleurs. Le tableau ci-dessus montre un « cercle des couleurs » agencé selon la longueur d’onde de manière à ce que les couleurs diamétralement opposées soient complémentaires. Le vert occupe une large bande en plus d'être plus lumineux. Au contraire, le jaune ne couvre que 20 nm dans le spectre et il nous apparaît étonnamment clair, à un point tel qu’il est difficile de lire un texte imprimé en jaune sur du papier blanc. On a constaté que le vert jaunâtre (555 nm) était la couleur la plus visible en plein jour. Cela s'explique car elle correspond à la moyenne des zones de sensibilité maximale des cônes rouges et verts, ces zones étant étrangement rapprochées. Nous voyons beaucoup moins bien le bleu et très peu le violet. Le vert turquoise (507 nm) est le plus visible sous un très faible éclairage à cause des « bâtonnets », qui ne perçoivent que cette couleur. Seuls les daltoniens confondent le rouge et le vert, mais tous les humains sont pour ainsi dire daltoniens en ce qui concerne le violet. C'est qu'une longueur d’onde précise de 380 nm leur semble identique à ce qu’ils voient si on mélange du rouge à 760 nm et du bleu à 470 nm. Notez que 760 est le double de 380, ce qui donne à penser que l'œil voit du bleu et que l’ajout de rouge est dû à un effet d’harmonique. Une autre hypothèse serait la participation des bâtonnets, et encore une autre la faiblesse ou l’absence du vert, que le cerveau pourrait interpréter comme étant du rouge. Par ailleurs, les objets violets, comme la petite violette des bois, réfléchissent aussi une forte proportion de rouge. Ils semblent donc violets parce qu’ils absorbent le vert. Tout comme les objets magenta ou pourpres, leur couleur n’est pas purement spectrale : elle résulte de l’addition de longueurs d'onde très éloignées. Si ces longueurs d'onde varient à cause de l'éclairage, leur couleur apparente variera aussi. C'est l'exemple extrême d'une couleur dite « métamère ». Cette particularité est capitale : elle permet de refermer le « cercle des couleurs » en utilisant l’indigo (bleu violacé) et le rouge pour reproduire le violet. On obtient alors en prime le magenta et le pourpre, qui sont absents du cercle des couleurs montré ci-dessus. Les couleurs complémentaires. Un objet nous semble coloré parce qu’il réfléchit la lumière de la même couleur. On a vu que c’est sans doute plus exactement que c’est parce qu’il absorbe toute cou leur complémentaire. On a constaté que ce phénomène était dû à plusieurs causes mais « l’effet bulle de savon » (des rayons réfléchis et annulés par interférences destructives) est souvent impliqué.C'est pourquoi un objet vert a deux couleurs complémentaires visibles différentes, le rouge et le violet. Il élimine ces deux couleurs. Celles qui sont le moins éloignées de la couleur de l’objet sont partiellement réfléchies. Étonnamment, pour reproduire le vert émeraude, l’ajout de lumière jaune et bleue en quantités moindres est normal. Ce n’est pas nécessairement catastrophique : c’est plutôt l’ajout de rouge qu’il faut éviter à tout prix. Un écran qui afficherait du vert émeraude sur les lignes de rang impair et à la fois du jaune et du bleu sur les lignes de rang pair continuerait de sembler vert, et ce vert semblerait étonnamment saturé. Ce serait la même chose pour les trois autres couleurs. Il s'agit là d'une particularité remarquable qui milite fortement en faveur d'une norme à quatre couleurs. Cela permettrait de simplifier la construction des écrans des téléviseurs et des ordinateurs, puisqu'on peut n'utiliser que deux couleurs par pixel au lieu de trois. Cela permet du même coup de réduire les données numériques requises. Il vaut mieux utiliser quatre couleurs primaires. Ainsi, lorsque vient le temps de mettre au point un système capable de reproduire les couleurs, que ce soit sur écran ou sur papier, il importe de surmonter toutes ces anomalies et même d'en tirer parti quand c'est possible. Si les procédés actuels présentent des défauts, c'est précisément parce qu'ils n'y arrivent pas. Même si la chose va de soi, très peu de gens proposent d'utiliser quatre couleurs « primaires » au lieu de trois seulement. Cela signifie que les écrans comporteraient (idéalement) quatre couleurs par pixel et que les imprimantes utiliseraient quatre couleurs d'encre, qui seraient les mêmes. J'en conviens, ce virage radical ne serait pas de tout repos, mais il permettrait d'obtenir des résultats supérieurs aussi bien sur écran que sur papier. Certains diront que le jeu n'en vaut pas la chandelle. Pourtant, les avantages d'un tel virage sont nombreux.
Les quatre couleurs doivent être complémentaires deux par deux. L'adoption d'une norme à quatre couleurs est avantageuse pour un grand nombre de raisons ; mais il faut réaliser que lorsque vient le temps d'afficher ou de numériser les images, c'est la présence des couleurs complémentaires qui permet d'en profiter au mieux. Lorsqu'on mêle sur un écran deux couleurs complémentaires à forte intensité, on obtient du blanc, qui n'est donc pas nécessairement un mélange de toutes les couleurs. Ce n'est pas tout à fait vrai, mais on peut compenser. De plus, l'œil mêle très intimement les couleurs de deux pixels voisins alors qu'il distingue nettement leur luminance. On verra plus loin que cette particularité permet de réaliser des écrans qui n'affichent que deux couleurs complémentaires par pixel sans pour autant réduire significativement leur efficacité. Cela réduit d'autant les données numériques. La longueur d’onde complémentaire « lc » d’une longueur d’onde quelconque « l » correspond aux trois quarts de celle-ci ou à la réciproque. La progression établissant quatre couleurs qui soient complémentaires deux par deux est basée sur la racine carrée de trois quarts, qui correspond aussi au sinus de 45° (0,866). C'est ainsi qu'il faut choisir l'indigo (450 nm) pour obtenir : le vert émeraude (450 / 0,866 = 520 nm) ; le jaune (520 / 0,866 = 600 nm) et le rouge (600 / 0,866 = 693 nm) en soulignant que les couleurs rouge et indigo sont celles des écrans actuels à peu de choses près. On verra plus loin que pour des raisons techniques, on a sans doute choisi un rouge légèrement orangé, peut-être à cause des pigments utilisés dans les écrans cathodiques. lc = l * 0,75 ou lc = l / 0,75 est complémentaire (si cette couleur est visible). l1 =
l2
* 0,866 ou l2 = l1
/ 0,866 fixe les quatre couleurs,
selon le sens de la progression. Les
couleurs rouge et bleu indigo utilisées actuellement
devraient donc être
conservées à peu de choses près. C’est le vert lime qui pose problème : avec les téléviseurs
actuels, il monopolise plus
de la moitié de la luminance. On peut donc prévoir que si
on divise ce vert lime en deux couleurs convenablement espacées, on
obtiendra quatre couleurs qui seront nettement plus équilibrées. Ces
deux couleurs sont le jaune et le vert émeraude, et chacune d'elles
demeure malgré tout plus lumineuse que le bleu. Les
défauts de la
norme à trois couleurs. Si on avait obligé le peintre Rubens à n’utiliser que trois couleurs, il aurait été malheureux. Il adorait les couleurs vives et il avait certainement constaté qu’un mélange « salit la couleur ». Cette expression a été utilisée par les peintres Impressionnistes pour faire valoir qu’il valait mieux juxtaposer les couleurs, d'où le « pointillisme ». Ils avaient raison, mais bien sûr ils n’ont pas fait l’erreur de se limiter à trois couleurs. L’imprimerie et l’écran n'utilisent pour l'instant que trois couleurs, et ce ne sont pas les mêmes. Si l’image apparaissant sur l’écran est reproduite par l’imprimante, il faut refaire le mélange et le résultat est souvent déplorable. Si ça vous amuse, essayez d'imprimer le cercle des couleurs montré plus haut. Vous verrez bien pourquoi Photoshop parle de « couleurs non imprimables ». En
fait, rien ne peut remplacer exactement
une couleur véritable saturée à 100% (celle d'un laser), pas même des points juxtaposés dont la couleur
est voisine. Pour le comprendre, il faut refaire l’expérience bien
connue : on colore la moitié d’un cercle avec du rouge et l’autre
moitié avec le vert complémentaire. Si on le fait tourner rapidement,
on verra que les deux couleurs s’annulent et donnent un gris neutre.
Mais si on utilise un vert lime, la couleur du disque devient jaunâtre.
Elle sera plus franchement orange si on utilise du jaune. On en déduit
que plus les deux couleurs utilisées sont proches l’une de l’autre,
plus la couleur de synthèse est saturée. Dès le départ, il est donc avantageux
d'utiliser quatre couleurs primaires plutôt que trois. La saturation d’une couleur obtenue à l’aide du mélange de deux autres dépend de la position de ces dernières sur le cercle des couleurs montré plus haut. Dans un système à trois couleurs, ceci mènerait à une saturation de 50 % seulement comme l’indique un triangle équilatéral inscrit dans un cercle (le sinus de 60° est 0,5). Or le rouge et l’indigo sont trop rapprochés, ce qui est évident dans « l’espace colorimétrique XYZ » élaboré par la CIE en 1931. Puisque le rouge et l’indigo occupent le même espace que dans un système à quatre couleurs, le vert prend trop de place : le triangle qui rend compte des mélanges à l’intérieur du cercle des couleurs n’est plus équilatéral. C’était prévisible, ce système présente des défauts importants. Au contraire, la norme à quatre couleurs produit un carré véritable. D'ailleurs, la saturation n’est pas complète même dans un système à quatre couleurs. Elle est quand même nettement meilleure : un carré inscrit dans un cercle indique une saturation de 70,7 % (le sinus de 45° est 0,707). Mais cette fois-ci, comme on le verra plus loin, c’est beaucoup plus proche de ce que la nature elle-même a prévu. Il faut savoir par exemple qu'une fleur dont le jaune présente un maximum de saturation reflète quand même des quantités non négligeables de rouge et de vert. Si sa couleur apparaît jaune, c'est surtout dû au fait que le bleu en est totalement absent. C'est pourquoi une caméra numérique à quatre couleurs n'enregistrera pas de bleu. Mais il faut réaliser qu'elle enregistrera du rouge et du vert de toutes façons : c'est inévitable, mais c'est surtout incroyablement avantageux. C'est ainsi que le fait de placer du jaune dans un pixel sur une ligne totalement exempte de bleu d'une part, et de placer du rouge et du vert en quantités égales dans le pixel voisin, sur la ligne suivante, produit quand même du jaune très convenable (sinon parfait) sans nuire à la résolution de l'ensemble. Il est très avantageux de ne numériser et de n'afficher que deux couleurs par pixel, ce qui permet d'utiliser des écrans contenant davantage de pixels. Il en résulte toujours un gain appréciable, soit dans la définition de l'image, soit dans la quantité de données numériques requises. Nos yeux fonctionnent mieux que les caméras. Quelle que soit la façon dont nos yeux fonctionnent, nous savons qu’ils sont capables d’évaluer toutes les couleurs avec une précision remarquable. Il ne faut pas se laisser prendre au piège : il y a trois types de cônes présents sur notre rétine mais il serait absurde d’en déduire qu’on peut les tromper en n’utilisant que trois couleurs. Notre cerveau est une merveilleuse machine capable d’interpréter, à notre insu, ce que ces cônes perçoivent. On sait que ces cônes sont sensibles au jaune verdâtre (565 nm), au vert lime (550 nm) et à l’indigo (440 nm). Première anomalie, et elle est de taille : il n’y a pas de cônes sensibles au rouge spécifiquement. Deuxième anomalie, tout aussi importante : le jaune nous apparaît bien différent du vert et du rouge. Pourtant, on devine très bien au contraire que la couleur turquoise est voisine du vert et du bleu. Il est donc probable que le cerveau identifie le jaune par l’absence de bleu dans une mélange rouge-vert. On peut aussi penser que les bâtonnets, actifs en lumière faible, le demeurent au moins partiellement en plein jour : le cerveau interpréterait alors l’absence de leur fréquence particulière (507 nm) par le rouge, même dans le cas du violet véritable de l'arc-en ciel. En effet ce violet ne contient pas de rouge et ce sont exclusivement les cônes du bleu indigo qui sont alors excités : autrement, le violet devrait nous sembler bleu indigo à moins qu'il ne se produise un effet d'harmonique. Si cela devait se confirmer, nos yeux identifieraient en réalité quatre couleurs, et la présence de cette fréquence des bâtonnets sur l'écran serait doublement avantageuse. Peu importe l’explication qu’on trouvera, on devra admettre qu’il est avantageux d’utiliser quatre couleurs. Les pionniers de la trichromie (Young, Helmholtz, Grassman) ont énoncé des lois et proclamé qu’on pouvait reproduire « toutes » les couleurs à l’aide de trois seulement. Mais au fil des ans, les chercheurs ont constaté qu’en réalité il était impossible d’obtenir certains mélanges. De plus, ils rencontrent des difficultés considérables, sinon insurmontables, pour atténuer les anomalies du système. Ceux qui savent traiter les couleurs sur leur ordinateur devraient essayer de mêler le vert lime et l’indigo dans le but d’obtenir la couleur turquoise. Hélas, elle sera terne, surtout si l'on maintient la luminosité à un niveau constant. Parce que le vert lime (donc jaunâtre) est beaucoup plus lumineux que le bleu et qu'il en est très éloigné dans le spectre, les mélanges sont imprévisibles, surtout quand vient le temps de les imprimer. Au contraire, avec quatre couleurs, l’ajout de l'indigo au vert émeraude produirait cette couleur turquoise vive et fascinante qu’on peut observer sur la bande alaire des sarcelles. Nos écrans actuels n'arrivent pas non plus à reproduire correctement la couleur orange. Elle serait avantageusement reproduite avec du jaune et du rouge. Vous constaterez sur le cercle montré plus haut qu'elle est vaguement brun pâle si vous la comparez à la couleur d'une orange véritable bien éclairée. Quatre couleurs au
lieu de trois. À la suite d’Ewald Hering, la Suède a adopté et fait breveter un système permettant d’identifier toutes les couleurs à partir de quatre. Le choix de ces couleurs est arbitraire, mais puisque le rouge, le jaune, le vert et le bleu sont des couleurs dites « psychophysiques », que tout le monde reconnaît, elles s’imposent à coup sûr. Hering avait noté que les couleurs devraient être complémentaires deux par deux. Toutefois, la codification adoptée est discutable. Le solide proposé est biconique, mais tout dépend en réalité des conventions et des procédés de reproduction. À mon sens, la norme CIE L*a*b* est plus logique. S'il existait un écran idéal, toutes ses couleurs pourraient être affichées sur la surface d'un cylindre et à l'intérieur, de la plus sombre à la plus claire en partant de la base. Le cylindre est en effet le seul solide capable de représenter chaque couleur dans toutes ses valeurs de luminance. La peinture à l'huile ne permet qu'un cône parce que les pigments absorbent d'autant plus de lumière que la couleur s'assombrit. Un écran RGB ne permet plus d'afficher ce cône en entier : sa base est forcément triangulaire. Elle est avantageusement carrée s'il y a quatre couleurs primaires, et la plus grande hauteur du cône indique que le contraste est meilleur. Un meilleur contraste. En réalité, le contraste peut être meilleur à la condition d'afficher réellement les quatre couleurs dans le même pixel et de ne faire intervenir les troisièmes et quatrièmes couleurs que si nécessaire. En effet, les filtres ne sont pas parfaitement sélectifs et une caméra quadricolore enregistre toujours au moins trois couleurs et même quatre dans le cas des couleurs secondaires. La solution consiste à faire intervenir un algorithme qui redistribue les couleurs au mieux. Cela permet de conserver la pleine saturation des couleurs sur une échelle plus grande ; et à partir de ce point les autres couleurs peuvent intervenir pour reproduire les teintes les plus lumineuses et un blanc plus éclatant. C'est ainsi qu'on obtient des couleurs plus vives et un meilleur contraste, mais ce n'est pas nécessairement souhaitable parce qu'il faudrait idéalement reproduire les choses telles que nous les voyons. D'un autre côté, pour y arriver, il peut devenir nécessaire d'intervenir. En somme, il faudrait respecter leur contraste et leurs couleurs véritables. De plus, une photographie de grande qualité devrait pouvoir être assombrie ou éclaircie dans le but de distinguer ce qui se cache dans ses zones les plus sombres ou les plus claires. À première vue, il faudrait donc codifier la luminance sur une échelle supérieure à 256, peut-être 512 et même 1024... Malheureusement, le cylindre est utopique parce qu'il nécessiterait beaucoup plus de données et qu'on n'arrivera sans doute jamais à construire un écran capable de reproduire toutes ces couleurs. On peut difficilement éviter que la couleur d’un ballon rouge soit « lavée » et qu’elle apparaisse rose ou même blanche si le ballon est au soleil et si le sujet photographié est à l’ombre (et donc exposé en fonction de l’ombre). Si nos yeux continuent de voir ce ballon rouge, il devrait être possible de le reproduire en rouge même s'il est au soleil ; mais pour y parvenir, il faudrait codifier la luminance sur une échelle bien supérieure à 1024. En imprimerie, le contraste d'une épreuve dépend d'abord de l'éclairage, qui est en principe le même si on compare deux épreuves obtenues avec trois ou quatre couleurs d'encre. Il n'empêche qu'on aurait intérêt à augmenter l'éclairage si nécessaire pour profiter de la meilleure qualité des épreuves quadricolores. Comme on le montre plus loin, une norme à quatre couleurs conduit à un solide complexe à base carrée qui ressemble à une maison à quatre pignons et à toit conique vaguement pyramidal. Ce solide peut afficher la plupart des couleurs d'une manière satisfaisante, beaucoup mieux en tous cas que le système RGB. Les couleurs grisâtres sont logées à l'intérieur. Le blanc se situe au sommet et le noir, à la base. La norme L*a*b*. La Commission Internationale de l'Éclairage (la CIE) propose la norme L*a*b*, a et b étant deux axes permettant chacun deux couleurs, qui sont complémentaires, mais une seule à la fois. L'axe a contrôle le rouge et le vert et l'axe b, le jaune et le bleu. Cette norme convient parfaitement puisqu'elle propose quatre couleurs primaires. On verra que contrairement à ce qu’on pourrait croire, l’ajout d’une couleur ne complique pas la mise en place d’un nouveau système : il facilite même parfois les choses. |
L'ESPACE COLORIMÉTRIQUE
Si elles sont affichées dans un espace en deux dimensions, il n'est guère possible de représenter toutes les couleurs d'une manière ordonnée. On peut toutefois afficher toutes celles dont la luminance est la même. Cette luminance correspond aux données numériques et non pas à la luminosité particulière normale de chaque couleur. On conviendra dans cette page qu'il s'agit de la « luminosité relative », compte tenu du fait que le jaune, par exemple, est bien plus lumineux que le bleu. De plus, même en disposant de quatre couleurs plutôt que trois, il n'est pas possible de reproduire toutes les couleurs de l'arc-en-ciel avec leur maximum de saturation. Les couleurs secondaires, soit l'orange, le vert lime, le bleu turquoise et le violet ne sont qu'approchées, le sinus de 45° indiquant (en principe) une saturation de 70°. Puisqu'il y a quatre couleurs primaires, dont la saturation est complète , il devient possible de montrer toutes les couleurs de l'arc en ciel (et aussi le pourpre et le magenta) sur le périmètre d'un « carré chromatique ». La saturation des autres couleurs situées à l'intérieur du carré diminue à mesure qu'on s'approche du centre, qui affiche le gris moyen. Ce gris est obtenu en n'utilisant que le quart de la luminance de chacune des couleurs. Ne vous y trompez pas, même s'il ne correspond qu'à 25% de la luminance, il s'agit bien du gris moyen ; si vous observez l'ombre d'un écran, vous verrez bien que la transition entre le noir et le blanc se fait plus rapidement côté noir. Cela s'explique par le fait que notre œil enregistre la luminosité selon une échelle logarithmique, ce que l'ouverture relative des caméras selon ƒ/ 2, ƒ/ 4, ƒ/ 8, etc. confirme. Pourtant, il a fallu l'éclaircir dans l'image montrée ci-dessous, ce qui pourrait trahir une autre déficience du système RGB. Puisque votre écran n'affiche que trois couleurs, vous ne verrez dans le carré chromatique montré ci-dessous qu'une approximation de ce qu'il est possible d'obtenir avec quatre couleurs primaires. En particulier, les couleurs orange, vert émeraude et turquoise seraient bien plus justes : |

Le carré chromatique quadricolore (ou tétrachrome) peut être évalué selon la norme CIE L*a*b*.
Ici, l'axe a (rouge, vert) est l'axe vertical, l'axe b (jaune, bleu) étant horizontal.
Ces quatre couleurs primaires permettent d'afficher un carré, mais pas un cercle chromatique complet.
Les couleurs de ce cercle peuvent être précisées autrement en leur attribuant un angle et une saturation.
L'image ci-dessous montre que votre écran RGB ne peut afficher qu'un triangle :
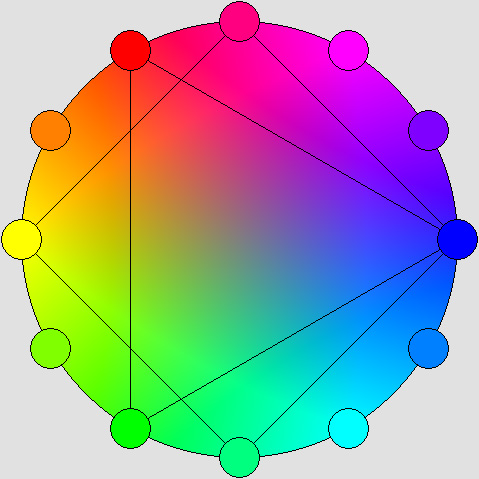
La saturation de toutes les couleurs représentées à l'extérieur du triangle est incomplète.
En plus clair, ces couleurs ne peuvent pas être reproduites ; mais le jaune et le violet font exception.
Le bleu est beaucoup plus sombre, ce déséquilibre conduisant à des anomalies graves.
L'axe b (jaune, bleu) étant horizontal, l'emplacement du rouge sur l'axe a de la CIE ne semble pas correct.
De deux choses l'une, ou le rouge de votre écran est légèrement orangé, ou le rouge de la CIE est magenta.
Ci-dessus, le triangle chromatique RGB est équilatéral ; mais on le montre plutôt isocèle ci-dessous.
D'un point de vue géométrique, la surface d'un cercle de rayon = 1 est égal à pi, alors que la surface du triangle équilatéral inscrit vaut : ((2 * sin 60°) * (1 + cos 60°)) / 2, soit 1,3. Celle-ci vaut donc moins de la moitié (41,7%) de la surface du cercle. Cela indique que la saturation de plus de la moitié des couleurs n'est pas complète. Mais ce n'est pas tout : en principe, vis à vis les couleurs complémentaires (turquoise, jaune et violet), la saturation n'est que de 50% selon le cosinus de 60°. Il ne faut pas en conclure qu'un écran RGB ne peut guère afficher que la moitié des couleurs dans la zone de saturation maximum ; en effet, la saturation du jaune est manifestement complète dans le cercle de gauche ci-dessus. Or ce n'est pas normal : tout indique qu'en présence de vert et de rouge à parts égales, la sensation de jaune résulte de l'absence de bleu. De plus, on a vu que l'œil interprète un mélange de rouge et de bleu comme étant du violet. Le violet est donc parfaitement saturé aussi. Ce que l'œil voit ne se plie guère à la théorie... Le système RGB table donc sur deux particularités extraordinaires de l'œil. Malheureusement, le violet est pratiquement absent de notre environnement. Au contraire, les tons de vert sont très importants, et encore plus les tons orangés. Les
couleurs chamois, or, cuivre, café, coquille d'œuf, beige, ocre, saumon,
marron ou brun, et surtout la couleur de la peau correspondent
essentiellement à la couleur orange en proportions et luminosités
variables.
Tous ces tons très nuancés et très fragiles ont une importance primordiale
dans la plupart des images ; s'il faut les reproduire avec du vert, c'est hautement risqué.
Grâce au
jaune, ils en seraient notablement améliorés et beaucoup moins sujets à
des variations fantaisistes. S'il
est vrai que le rouge du système RGB est orangé dans les faits,
peut-être volontairement pour satisfaire à des contraintes physiques, la
distorsion selon le triangle isocèle montré ci-dessous n'a pas lieu.
Pourtant, ce rouge a l'air vraiment rouge. Si c'est bien le cas, c'est plutôt le
rouge de la CIE qui devrait être franchement magenta ; mais on n'en fait
mention nulle part. Là encore, c'est à l'œil qu'il faut se fier, et non
aux instruments de mesure. Il s'agit de faire en sorte que si on le
mélange au vert émeraude, ce rouge produise un ton de gris. Si
l'on devait préserver ce rouge orangé coûte que coûte, on pourrait
tout aussi bien décaler
toutes les autres couleurs dans un système à quatre couleurs. On aurait
successivement 665 nm (rouge orangé) , 576 nm (jaune
verdâtre, soit 665 multiplié par le sinus de 45° ou 0,866), 500 nm
(vert turquoise) et 432 nm (indigo). Mais
d'un autre côté, les couleurs traditionnelles des encres d'imprimerie
sont le magenta, le jaune et le cyan (turquoise). Le magenta pourrait donc
devenir la couleur incontournable aussi bien sur nos écrans qu'en
imprimerie. Dans ce cas la couleur de l'encre cyan devrait donc être
remplacée par deux couleurs beaucoup plus logiques, soit le vert et le
bleu. Un coup d'œil
aux deux diagrammes ci-dessous suffit pour se convaincre que le système
RGB laisse nettement à désirer. : |
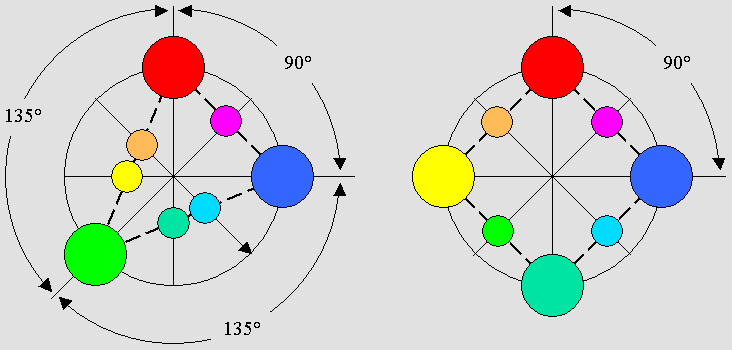
À gauche, la norme RGB à rouge franc produit un triangle isocèle où certaines couleurs sont triturées à l'extrême.
On a vu plus haut que le triangle devrait être équilatéral si le rouge de la CIE est plutôt magenta.
La figure de droite montre qu'une norme à quatre couleurs rétablit la symétrie grâce au carré.
Ce carré est plus proche du cercle chromatique ; il autorise des couleurs plus équilibrées et saturées.
LA MAISON DES COULEURS
On peut avantageusement représenter toutes les couleurs dans un espace en trois dimensions selon un « solide des couleurs ». On convient alors que la teinte fait référence à la longueur d'onde, et qu'elle peut donc varier de la plus sombre à la plus claire. Une teinte de vert en particulier peut présenter différentes valeurs luminance, mais différentes teintes de vert présentent plutôt des variations dans leur chrominance. Ces termes font référence ici à la codification numérique et non à la véritable luminosité ou chromaticité, ce qui nous permettra d'obtenir un solide plus uniforme. Il peut en effet exister toute une variété de ces solides selon ce qu'on veut en faire. Par exemple, la CIE a établi un solide d'après les couleurs que l'œil peut distinguer. Ce solide est très révélateur. Il a une forme bizarre, alors qu'un « œil parfait » devrait conduire à un solide parfaitement biconique. On peut tout aussi bien représenter les couleurs selon une sphère, mais celle-ci ne se prête guère à la codification numérique. Il faut en effet établir les valeurs selon un escalier, et parce que le nombre de couleurs primaires est limité on obtient finalement une pyramide à gradins à base triangulaire ou carrée. Notre but sera donc de construire un solide qui rend compte de la codification numérique. Il faut en premier lieu établir un axe vertical représentant l'échelle de gris et l'échelle de luminance pour les autres teintes. Le noir se situe à la base du solide, et le blanc au sommet, ce qui indique que les teintes aussi évoluent de la plus sombre à la base à la plus claire au sommet. On convient ensuite que la distance de cet axe sur un plan horizontal détermine la saturation de ces teintes, selon une échelle de chrominance. Un cône modifié. Selon
cette convention, il est évident que si le nombre de couleurs primaires disponibles
est presque infini (c'est le cas par exemple de la peinture à l'huile),
le solide qui en résulte ne peut être qu'un cône. Toutefois, sa base
devient un polygone dont le nombre de côtés diminue selon le nombre de couleurs
primaires utilisées. Puisqu'il y en a quatre, on obtient un cône tronqué à sa base de
manière à ce qu'elle soit carrée, et le restant du cône devient
vaguement pyramidal selon un angle de 45°. Dans ce
contexte, on peut prendre comme exemple la couleur rouge qui frôle le
noir, et qui est très difficile à distinguer d'une couleur verte qui
serait tout aussi sombre. La CIE préfère disposer les couleurs selon
que l'œil peut les distinguer ou non, et c'est très bien. Elle propose
donc un solide qui repose sur une pointe noire. Il n'empêche que la
saturation de ces deux couleurs est totale, et que c'est précisément
cette saturation qu'il s'agit ici de mettre en évidence, ce qui sera
très révélateur à mi-hauteur. C'est pourquoi le solide des couleurs
quadricolore présente une base carrée, qui est uniformément noire. En
deuxième lieu, on sait que chacune des couleurs qui est affichée sur
un pixel de l'écran peut varier sa luminance selon une échelle qui va généralement de 0 à 255.
Cette échelle est la même pour le jaune et le bleu, et il n'est pas
question ici de tenir compte du fait que le jaune est beaucoup plus
lumineux que le bleu. Il
va de soi que ce solide représente la luminosité relative
de chaque couleur, telle qu'un octet peut la représenter, sans tenir
compte de sa luminosité réelle.
Les couleurs secondaires sont plus lumineuses.
De
cette manière, si la luminance d'une couleur
primaire plafonne à 256, celle d'une couleur secondaire obtenue à
l'aide des deux couleurs voisines à pleine puissance plafonne plutôt à
512. Trois
couleurs à pleine puissance auront pour effet de porter le total à 768 et la couleur qui en résultera continuera de
présenter une saturation étonnante à cause de l'absence totale de la
couleur complémentaire. En pratique cependant, la caméra est incapable
de livrer les données numériques correspondantes. Cela ne peut être
rendu possible qu'en ayant recours à un algorithme de correction. Mais
c'est possible. Quelle que soit la couleur d'un objet (un ballon rouge au soleil, par
exemple), et pas seulement
s'il s'agit d'une couleur secondaire, on peut donc techniquement la préserver même lorsque sa
luminance atteint 75% du blanc le plus éclatant. Cette performance est tout
à fait impensable avec un écran RGB, tout simplement parce que
l'intervention même faible des deux autres couleurs a pour effet de
réduire irrémédiablement la saturation. Le blanc se situe au sommet à
1024 et il est
donc plus lumineux (toutes proportions gardées) que le blanc du système
RGB. Cela indique que le contraste de l'image est bien meilleur. Un avantage pour les manufacturiers et les diffuseurs. C'est
en tablant sur cette propriété remarquable des couleurs complémentaires
que je propose de ne tenir compte que de deux couleurs par pixel, en
alternant les axes a et b de la CIE. Je suis convaincu que ce n'est pas la
saturation des couleurs ni même le contraste qui séduiront les manufacturiers, mais bien l'économie qui en résulte dans la fabrication des caméras et des
écrans, sans oublier la réduction des données numériques. On
aboutit à un solide qui a l'aspect d'une maison carrée flanquée de
quatre pignons triangulaires et surmontée d'un
toit conique vaguement pyramidal, comme le montre la figure de droite
ci-dessous. C'est ce qu'on pourrait appeler la « maison des couleurs » : |
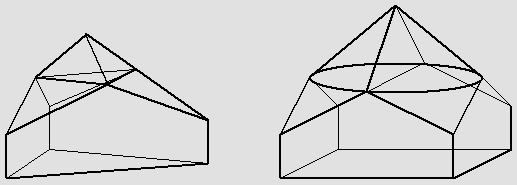
La figure de gauche montre que la base d'un solide chromatique RGB est un triangle isocèle.
À droite, le solide quadricolore (ou tétrachrome) ressemble à une maison carrée surmontée d'un toit conique.
Ce cône étant vaguement pyramidal, il sera représenté ici par une pyramide pour simplifier les graphiques.
Noter que la pointe supérieure est plus élevée, ce qui indique que le blanc est plus lumineux.
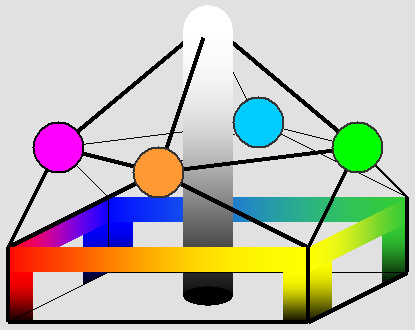
L'échelle de gris se situe au centre de la « maison des couleurs », le blanc étant au sommet.
Les couleurs primaires parfaitement saturées plafonnent très rapidement selon un carré.
Les couleurs secondaires plafonnent deux fois plus haut, aux quatre coins de la pyramide.
La saturation des couleurs secondaires orange et turquoise est bien meilleure qu'en mode RGB.
|
Ci-dessous, on a une vue semblable qui montre les teintes de la surface de ce solide avec plus de précision. Elle tient compte des différents mélanges possibles : |
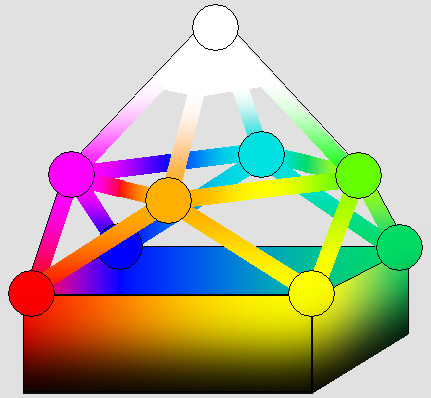
Certaines couleurs impossibles à reproduire en mode RGB le deviennent avec 4 couleurs primaires.
La saturation des huit couleurs primaires et secondaires est plus grande sur une large plage de luminance.
Toutes proportions gardées, le blanc est plus lumineux parce qu'il est composé de quatre couleurs.
Le contraste est meilleur ; les mélanges sont plus fiables et plus précis.
LA CODIFICATION NUMÉRIQUE
|
« Des millions de couleurs ! » Contrairement aux toiles de Rubens, les images numériques sont pour ainsi dire éternelles. Elles pourront être visionnées et copiées très loin dans l’avenir avec les mêmes qualités et les mêmes défauts. Aussi bien alors qu’elles aient le plus de qualités possible. À raison de 3 octets par pixel, les images BMP (bitmap) permettent plus de 16 millions de couleurs. Toutefois, les images JPEG et les vidéos MPEG-4 utilisent une compression astucieuse qui permet de faire pratiquement aussi bien avec beaucoup moins de données. On y travaille très fort si l'on se fie à ce qu'on raconte sur l'Internet. On aura fait faire preuve de beaucoup d’astuce pour faire tenir un film de 2 heures en haute définition véritable (1920 x 1080 pixels) sur un seul DVD, et le compte à rebours est commencé. Aux dernières nouvelles, deux systèmes différents sont en concurrence ; espérons qu'on ne revivra pas le cauchemar Bêta-VHS. Personnellement, je m'interroge sur la nécessité de vouloir à tout prix afficher ces 16 millions de couleurs, car c'est inutile et c'est toujours au prix d'une réduction significative de la résolution ou des dimensions de l'image. C'est que les données économisées sur la couleur permettent d'afficher bien plus de pixels : les images sont plus grandes et plus précises sans pour autant présenter d'anomalies perceptibles dans leurs couleurs. C'est donc avantageux. Il importe de dessiner les contours d'un objet avec précision, mais on peut très bien n'insister sur sa couleur exacte que si elle s'étale sur une grande surface. En pratique, la moitié des pixels d'une image peut être numérisée en échelle de gris seulement, selon un damier, sans que la différence ne soit perceptible. Il demeure possible de présumer de leur couleur d'après celle des quatre pixels colorés voisins. De la même manière, on peut compresser les données de manière à favoriser la luminance au détriment de la couleur. Le résultat n'est pas nécessairement catastrophique comme le montre l'illustration suivante :
Même deux couleurs complémentaires n'arrivent pas à séparer les pixels convenablement. Ces couleurs se mêlent si on les rapproche : leur nuance exacte n'a plus d'importance.
Si vous aimez l'aquarelle, prenez la peine de dessiner des cumulus en traits noirs indélébiles et colorez ce qui reste du ciel bleu avec le bleu pastel. Vous pouvez très bien (c'est même mieux !) y aller à large traits sans prendre garde aux limites exactes des nuages. Le principe qu'on peut en tirer est le suivant :
La compatibilité. Les caméras de la télévision actuelle, du moins celles qui respectent la norme NTSC en Amérique et dans de nombreux pays, enregistrent et transmettent déjà les quatre couleurs complémentaires déjà mentionnées. Cette affirmation peut sembler surprenante, mais elle est exacte. C’est dû au fait que pour préserver la compatibilité avec les anciens téléviseurs noir et blanc, on a continué de transmettre les signaux dits de « luminance ». On a simplement ajouté des signaux pour le rouge et le bleu dans la même bande passante de 6 MHz. On peut alors récupérer le vert lime par soustraction : luminance – (rouge + bleu) = vert lime. Mais on peut tout aussi bien obtenir le vert émeraude : luminance – rouge ; de la même manière on peut récupérer le jaune : luminance – bleu. En mode numérique pour la télévision à haute définition, sans doute par habitude, on a continué semble-t-il d'utiliser ce système même s'il ne s'imposait plus. Il serait donc possible là aussi de récupérer les quatre couleurs. La solution se situe donc simplement du côté des postes récepteurs, ce qui signifie que dès maintenant, on pourrait fabriquer des modèles qui affichent quatre couleurs. On pourrait même le faire à raison de deux couleurs par pixel. Étonnamment, ces couleurs sont disponibles mais elles se perdent. Une nouvelle codification. En utilisant seulement deux couleurs par pixel au lieu de trois, on réduit les données numériques ou on augmente le nombre de pixels, ce qui accroît la précision d’une image. On peut aussi montrer que la fameuse « trame » utilisée en imprimerie peut être éliminée parce que la norme CIE L*a*b* ne permet qu’une seule couleur par axe : à mi-chemin, on obtient du gris, qui peut être rendu avec l’encre noire. Là aussi il suffit donc d’alterner les couleurs complémentaires sur deux lignes. Certains
ne voudront pas croire que le fait d’alterner deux couleurs
différentes n’est
pas perceptible. Pourtant, tous les essais faits dans ce sens le
confirment : si on alterne le rouge et le bleu à luminosité
égale
sur deux lignes contiguës de l’écran d’un ordinateur, l’ensemble apparaît
violet et il est vraiment impossible (à la distance normale) de distinguer les couleurs séparément.
Mais on peut continuer de dessiner les contours de n’importe quel
objet en luminance selon chacune de ces lignes. La définition est donc
maintenue. Contre toute attente, un signal continu qui ne transmet que deux couleurs au lieu de trois peut être plus efficace pourvu qu'il tienne compte de quatre couleurs primaires. À données numériques égales, il peut transmettre une image plus grande, plus précise, plus contrastée, et dont les couleurs sont plus fidèles. Je n'ai pas les moyens de le vérifier. Je ne travaille pas dans ce domaine et il se peut que je divague. Vous étiez prévenus : je suis un délinquant. Mais si je ne m'abuse, la matrice CCD des caméras numériques pourrait comporter des cellules photosensibles disposées de la manière suivante : |
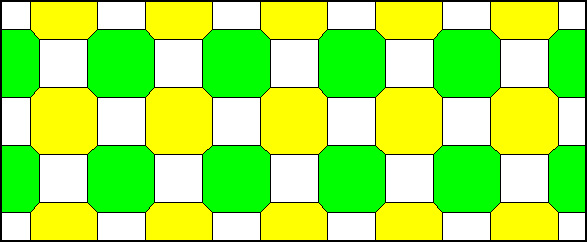
La caméra capte les pixels de cette manière, en évaluant trois types de zones.
Le zones montrées en blanc n'évaluent que la luminance.
Les filtres jaunes et verts permettent d'évaluer directement ces couleurs.
On évalue la couleur complémentaire par soustraction d'après la luminance des quatre pixels voisins.
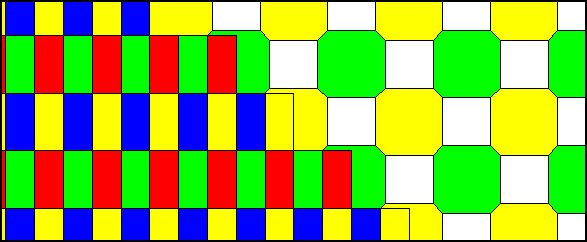
L'écran n'affiche que deux couleurs par pixel, et ces couleurs sont absentes sur la ligne voisine.
Un objet jaune, par exemple, reflète aussi du rouge et du vert, qui s'affiche sur l'autre ligne.
Ainsi, chaque ligne ne comporte que des couleurs complémentaires et sa luminance est correcte.
L'œil n'est pas incommodé par cette séparation car il mêle facilement les couleurs.
La norme HDTV est là pour rester. Dans le cas de la télévision, les nouveaux écrans plasma ou à cristaux liquides permettent d'effectuer le passage d'une image à l'autre de plusieurs manières. Le rayon cathodique ne pouvait afficher qu'un seul point réel à la fois, mais désormais on peut constamment rafraîchir les pixels selon une séquence complexe. Le clignotement est complètement éliminé : il n'est plus obligatoire de construire les caméras de manière à ce qu'elles suivent le balayage imposé par le rayon cathodique. C'est ainsi que la disposition des pixels dans les caméras conçues pour la télévision (et le cinéma numérique de demain) peut désormais être la même que celle proposée ci-dessus. Il existe d'ailleurs d'autres possibilités qui tablent aussi sur les couleurs complémentaires : je ne fais que proposer une méthode, mais ce n'est peut-être pas la meilleure. Pour limiter les données requises, il s'agit de transmettre le moins d'images possible, la norme de 24 images par secondes du cinéma étant semble-t-il une moyenne raisonnable. Mais il existe différentes manières d'entrelacer ces images, et les meilleures utilisent sans doute les propriétés étonnantes des couleurs complémentaires. La norme HDTV avec ses 1920 x 1080 pixels entrelacés (et un jour progressifs) se répand peu à peu. Hélas, beaucoup de nouveaux téléviseurs dont l'écran fait 16 : 9 n'affichent pas autant de pixels. Manifestement, les manufacturiers et les commerçants profitent de l'ignorance des consommateurs ! Il semble évident que cette norme sera toujours utilisée dans deux siècles. Je ne serais pas surpris que même les écrans des ordinateurs se convertissent à ce format dans un avenir prochain, car il est extrêmement performant et agréable. En fait, ce sont plutôt les grands écrans HDTV qui pourront être branchés sur l'ordinateur, un petit moniteur auxiliaire étant très utile pour les contrôler. Dans ce contexte, la mise au point d'écrans plasma ou à cristaux liquides à quatre couleurs primaires rafraîchies selon une séquence complexe mais efficace ne semble pas représenter un défi considérable. Les chercheurs travaillent d’arrache-pied pour mettre au point des écrans plats et légers qui soient en même temps efficaces et peu coûteux. Ils ont fait des pas de géant dernièrement, et il n’y a pas de doute qu’ils arriveront à faire encore mieux. Ceux que cette page aurait intéressés feraient bien de jeter aussi un coup d'œil à la page sur la courbure de champ. On y montre qu'il aurait fallu privilégier le champ cylindrique dès qu'on a commencé à produire des caméras numériques. Même les écrans devraient idéalement être faiblement cylindriques, de manière à ce que le spectateur puisse se situer au centre de courbure ; mais ce n'est pas vraiment nécessaire. Autrefois, le film ne permettait pas de réaliser des instantanés à l'aide d'une lentille ƒ/ 32 ou ƒ/ 64. Or non seulement les CCD électroniques sont plus sensibles, mais ils réagissent très bien à une telle ouverture car leur surface doit augmenter en proportion du disque d'Airy. Ce n'est pas le cas du film, qui exige des lentilles lumineuses de ƒ/ 8 ou moins qui sont hélas très imprécises surtout sous une certain angle de champ. Je propose donc de profiter de cette nouveauté pour construire des caméras à surface photosensible cylindrique (elle sera éventuellement sphérique dans un avenir éloigné), qui seront incroyablement précises. On bénéficie dans ce cas de tous les avantages d'un sténopé sans ses inconvénients.C'est ce que j'appelle un « sténopé à lentille », qui n'est efficace qu'un version numérique. La précision quasi-parfaite (on peut même apodiser le disque d'Airy), le très grand angle de champ sans distorsion et l'extrême profondeur de champ sont ses atouts majeurs. Ceux-ci sont attribuables aux lentilles à champ courbé et à petite pupille (2 mm au maximum). Bien
évidemment, ces caméras numériques devraient tenir compte de quatre couleurs
primaires. Alors on peut penser qu'il ne sera jamais possible de faire
mieux même dans un avenir éloigné, à des poussières près. Sauf si
les CCD nous réservaient d'agréables surprises...
UN
CODE DE RECONSTRUCTION On
peut aussi élaborer un code de reconstruction élémentaire qui
permet de ne numériser que le quart des données d'une image, dont les
dimensions s'en trouvent réduites de moitié. Ce code ne contient
que des instructions limitées. Il permet d'améliorer
étonnamment les performances lors de la reconstruction de
l'image, qui se traduit par un agrandissement. Il
remplace avantageusement la méthode actuelle d'agrandissement dite «
bicubique ». Supposons
par exemple qu'on reçoive une photographie faisant 640 x 480 pixels en format
JPEG. Pour obtenir une excellente qualité, cette image exige environ 100 K.
Mais elle est fournie avec un code de reconstruction additionnel de 30K qui permet de doubler
ses dimensions à 1280 x 960 pixels. Si
vous avez l'habitude des photographies ou des vidéos, vous savez qu'il est
avantageux d'agrandir l'image en choisissant l'option bicubique. Cela permet
d'obtenir une image plus naturelle qui estompe les transitions et qui fait même
ressortir certains détails qui n'étaient pas très visibles sur l'épreuve
originale. Toutefois, cette copie sera très semblable. Le
fait de doubler les dimensions d'une image oblige à quadrupler le nombre de
pixels, ce qui fait que l'image devrait en principe exiger 400 K plutôt que
100. Dans cette image, il serait utile de savoir quelle devrait être la couleur des
nouveaux pixels. On note qu'il en existe de deux sortes. Certains sont situés
entre deux pixels connus seulement, et ils sont deux fois plus nombreux que ceux
qui sont entourés de quatre pixels
connus. Dans
l'image ci-dessous, on suppose que les pixels connus sont les pixels noirs. Les
pixels gris sont ceux qui n'ont que deux voisins connus ; eux seuls sont
disposés en quinconce. Les pixels blancs
sont entourés de quatre pixels connus :
|

Seule, la couleur des pixels noirs est connue.
Les pixels gris sont imbriqués et ils représentent 66% des pixels à décoder.
Il s'agit d'élaborer un code qui permettra d'identifier le pixel voisin qui convient le mieux.
|
La plupart du temps, un pixel fait partie d'un ensemble et sa luminance est apparentée à celle d'au moins un de ses voisins. Le but du code est d'identifier le pixel dont la luminance convient le mieux. Ce renseignement nécessite un minimum de données, mais il fait toute la différence. 1280 x 960 pixels représentent 1 228 800 pixels dont les trois quarts, soit 921 600, sont à évaluer. La luminance des pixels gris (66%, soit 614400) montrés ci-dessus peut être identifiée grâce à la seule valeur 0 ou 1, qui indique s'il faut préférer le pixel supérieur ou inférieur, ou le pixel gauche plutôt que le pixel droit selon le cas. Un octet permet ainsi de codifier 8 pixels. On a 614400 / 8 = 76800 octets (76,8K). La luminance des pixels blancs (307200) peut comporter quatre valeurs d'après leur quatre voisins, et un octet permet donc d'en codifier 4. Cette opération nécessiterait : 307200 / 4 = 76800 octets (76,8K) pour un total de 153,6K. C'est peut-être trop. On peut opter plutôt pour un code à deux valeurs (0 ou 1) qui indique simplement s'il faut choisir le plus clair ou le plus sombre de ces quatre pixels. Alors le code de reconstruction complet ne nécessite que 921600 / 8 = 115,8K. C'est donc au départ mieux que les 300K additionnels qu'une image agrandie compressée en JPEG exigerait. Toutefois, ce code peut être compressé à son tour, et c'est pourquoi je suppose qu'il n'exigerait peut-être que 30K. Ce serait par exemple en ne codifiant que les pixels qui s'écartent sensiblement de ce que l'agrandissement bicubique proposerait. J'ai pris la peine d'évaluer la chose sur une photographie normale et tout indique que les trois quarts des pixels au moins ne souffrent pas beaucoup de l'agrandissement bicubique. Peu de pixels ont vraiment besoin d'un code, mais il faudra savoir comment les identifier. Ce code convient à merveille à la télévision en haute définition. Il est bien évident que ce code ne peut être élaboré que si la photographie originale comportait effectivement quatre fois plus de pixel, donc ici 1280 x 960. On peut faire remarquer en particulier que de nombreux téléviseurs à écran large 16 : 9 effrontément mis en vente sous l'appellation « haute définition » n'affichent la plupart du temps que 720 lignes horizontales et même aussi peu que 480 (le format DVD numérise 720 x 480 pixels dans tous les cas et il ne fait qu'étirer l'image si elle est en 16 : 9). La véritable télévision en haute définition HDTV devrait en afficher 1080. Il serait donc possible de filmer une scène en haute définition et de ne transmettre que le quart des données, à la condition de transmettre en plus un code de reconstruction pour les écrans 1920 x 1080. L'illustration ci-dessous montre comment la réduction d'une image à la moitié de ses dimensions originales puis son agrandissement en mode bicubique provoque un flou. C'est ainsi que la lettre « R » est reconstituée avec une certaine élégance. Cela démontre que ce procédé est efficace en estompant les irrégularités. Mais qu'on ne s'y trompe pas : même si la nouvelle image est agréable à regarder, ce n'est plus l'image originale. Elle est floue. Elle a perdu beaucoup de sa résolution. Au contraire, les pixels épargnés montrés au bas de l'illustration sont les pixels originaux, et le code de reconstruction permet de récupérer les pixels manquants avec une efficacité remarquable. |
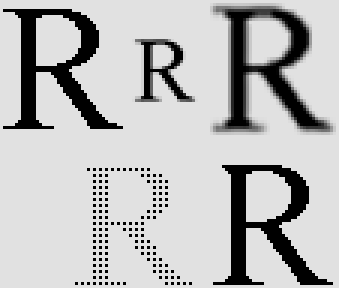
L'image originale de la lettre « R » figure dans le coin supérieur gauche.
À sa droite, l'option bicubique provoque un flou lors de sa réduction puis de son agrandissement.
En bas et à gauche, les espaces libres entre les pixels épargnés peuvent être récupérés grâce au code.
À droite, l'image reconstituée est pratiquement identique à l'image originale.
Mais les lignes horizontales ou verticales qui ne font qu'un pixel sont éliminées une fois sur deux.
|
On constate que les points isolés sont effacés trois fois sur quatre. Les lignes horizontales ou verticales dont la largeur n'est que d'un seul pixel le sont une fois sur deux. Leur luminance est remplacée par la luminance des pixels voisins, ce qui limite les dégâts. Si l'image à traiter présente une granularité fine, il en résultera un artéfact très visible. Par exemple, les images GIF à couleurs indexées en nombre limité et ayant subi une diffusion (dithering) sont celles qui en souffriraient le plus. Croyez-le ou non, j'ai mis une heure à agir comme le ferait le code de reconstruction en comblant point par point, grâce à Photoshop, les lacunes du « R » montré en bas, à gauche. Ce n'est qu'après avoir terminé ce travail de Bénédictin que j'ai réalisé que l'image finale était identique à l'image originale, à l'exception des trois pixels de la pointe supérieure gauche du « R ». Ces pixels ont donc été effacés. Si le rang de la ligne noire la plus basse avait été impair, ce sont plutôt les pixels situés aux extrémités de cette ligne qui auraient été effacés. Cette image ne comporte que du noir et du blanc. Dans le cas d'une image en couleurs normale, il est très rare qu'elle comporte des lignes fines et droites parfaitement verticales ou horizontales ; une ligne oblique dont la largeur ne fait qu'un pixel serait au minimum affichée en pointillés. Mais il arrive fréquemment que la couleur (et non la luminance) d'un pixel donné soit relativement différente de celle des pixels voisins. Le but du code est de récupérer sa luminance et non sa couleur, et c'est pourquoi il vaut mieux choisir entre le pixel le plus clair et le plus sombre. Le résultat ne peut pas être parfait, mais la résolution de l'image sera préservée au mieux sans qu'il ne se produise de différence remarquable dans le résultat final. On peut réduire les défauts, mais c'est au prix d'un code plus imposant. Il existe toute une variété de méthodes pour compresser les données. Si je montre celle-ci dans une page qui traite de la couleur, c'est précisément parce que la norme à quatre couleurs permet, contre toute attente, de compresser les données numériques. Puisque c'est sans doute la possibilité de réduire les données qui incitera les responsables à adopter une norme quadricolore, aussi bien jouer cette carte à fond. |
|
Gabriel LaFrenière, Bois-des-Filion en Québec. Sur l'Internet depuis septembre 2002. Dernière mise à jour le 24 octobre 2009. Page d'accueil : La matière est faite d'ondes. Courrier électronique : veuillez consulter cet avis. La théorie de l'Absolu, © Luc Lafrenière, mai 2000. La matière est faite d'ondes, © Gabriel Lafrenière, juin 2002. Optique des miroirs, © Gabriel Lafrenière, juillet 2001. ISBN 2-9806972-2-2 |