LE STÉNOPÉ
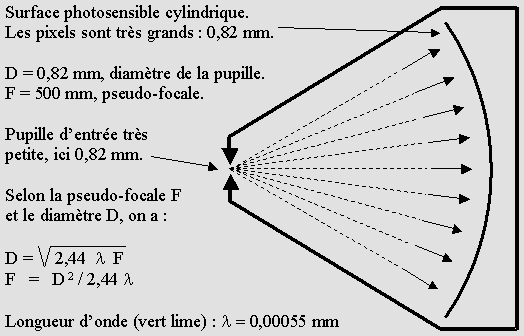
La célèbre « caméra à trou » sans lentille.
![]()
![]() Page d'accueil : La matière est faite
d'ondes.
Page d'accueil : La matière est faite
d'ondes.
|
Avertissement. Cette page appartient à une suite qui se nomme « L'optique délinquante ». Dans ces conditions vous ne pouvez pas vous attendre à ce qu'elle soit conforme à l'optique traditionnelle ou académique. Parce que je suis un chercheur, vous pouvez même vous attendre à ce qu'elle comporte certaines erreurs, puisque c'est le lot des chercheurs de s'égarer en sortant des sentiers battus. En effet, peu de chercheurs trouvent, comme l'indique ce mot du général de Gaulle : « Des chercheurs qui cherchent, on en trouve. Mais des chercheurs qui trouvent, on en cherche ». Une invention chinoise. Le sténopé est une caméra sans lentille, celle-ci étant remplacée par une simple perforation dont le diamètre est très faible. Le terme anglais "pinhole camera" est donc plus pertinent que l'expression italienne camera obscura ou chambre obscure, qui a conduit au mot caméra. Le terme français sténopé vient du grec et signifie "petit trou". Il s'agirait d'une invention chinoise très ancienne (environ 500 ans avant notre ère). On le retrouve ensuite dans la Grèce antique. Au moment de la Renaissance italienne, il a permis d'établir les règles de la perspective selon le fameux point de fuite. La surface photosensible peut être plane, car la perforation est en réalité la pupille d'entrée classique des opticiens. Toutefois on préférera assimiler dans cette page cette perforation à la pupille de Schmidt, cette dernière étant placée par définition au centre de courbure d'un système optique dont les éléments sont concentriques. On trouvera des exemples à la page sur la courbure de champ. C'est ce qui justifie la courbure de la surface photosensible proposée un peu plus loin. Des images diffuses et à faible résolution. On verra plus loin que la pseudo-focale d'un sténopé n'est qu'un compromis. Elle fait appel aux propriétés de la diffraction de Fresnel, que l'ouverture circulaire d'un sténopé reproduit à partir d'un point lumineux éloigné. Le faisceau lumineux qui en résulte est identique à celui d'un laser de bonne qualité. Ce qu'on appelle plus spécifiquement la diffraction de Fraunhofer est en réalité une tache d'Airy classique, mais elle ne se forme qu'à grande distance, ce qui n'est pas le cas ici. Si donc on se réfère uniquement à la diffraction de Fresnel, on a plutôt affaire à une tache d'Airy en voie de formation dont le premier anneau n'est pas encore détaché du disque central. À la distance jugée acceptable pour y situer la pseudo-focale, la luminosité de cet anneau est encore anormalement élevée. C'est aussi le cas des autres anneaux, mais dans une moindre mesure. Même à grande distance, la résolution du sténopé n'atteint donc pas tout à fait celle des caméras à lentilles, qui profitent d'une tache d'Airy idéale. Cela suppose une caméra énorme faisant environ un mètre, mais capable de distinguer les deux mégapixels d'un écran standard HDTV. Avec un petit sténopé ordinaire, la résolution n'atteint guère que le très ancien et détestable standard 640 x 480 pixels. On verra plus loin qu'il existe quelque part à mi-chemin une solution à la limite du raisonnable. La diffraction. Mais surtout, le sténopé doit composer avec un phénomène que Ludwig von Seidel n'a pas cru bon d'ajouter à sa fameuse liste de 1845 malgré le fait qu'il s'agisse manifestement d'une aberration optique importante : la diffraction. On pourrait parler de la diffraction de Fresnel, quoique cette expression désigne l'ensemble du réseau de diffraction que produit une ouverture circulaire équiphasée. Ici, il est plutôt question de la première frange de diffraction, celle qui est causée par les bords de l'ouverture. On voit ci-dessous que la lumière est plus fortement diffusée à cet endroit que partout ailleurs. Cette lumière est distribuée dans toutes les directions. Elle affecte bien sûr localement la tache d'Airy et ses anneaux, mais elle réduit aussi le contraste de toute l'image.
La diffraction de Fresnel. À droite, la diffraction dite de Fraunhofer se traduit par une tache d'Airy en voie de formation.
Le rapport du rayon d'un cercle à sa surface varie selon son carré selon la formule bien connue : S = pi * R 2. C'est pourquoi le rapport de la circonférence du trou du sténopé à sa surface augmente de manière exponentielle. Plus le trou du sténopé est petit, plus cette diffraction causée par les bords de l'ouverture est importante. Cela dépend aussi de la longueur d'onde, le violet étant moins affecté que le rouge. Les photographes admettent généralement qu'il vaut mieux ne pas fermer à plus de ƒ/16, mais ils devraient être informés que ce principe n'est valable qu'avec une caméra standard. En réalité, c'est le diamètre de la pupille d'entrée (c'est à dire le trou du sténopé ou l'iris du diaphragme) qui fait toute la différence, même une ouverture relative de ƒ/100 n'étant pas en soi impraticable avec une pupille de deux ou trois millimètres de diamètre. Celle-ci suffit généralement pour produire des photographies convenables, mais ses dimensions ont aussi un lien avec la profondeur de champ et avec le nombre de pixels qu'on peut en obtenir. Elles ont aussi un forte incidence sur les autres aberrations de Seidel. En général, une petite pupille (et donc le sténopé) exige un grand angle de champ alors qu'un téléobjectif exige une grande pupille qui limite sa profondeur de champ. La photographie, c'est donc d'abord et avant tout l'art du compromis, d'où l'utilité de bien connaître ces phénomènes. Dans le cas du sténopé, le trou fait généralement moins d'un millimètre. La profondeur de champ atteint donc un maximum, mais il faut un grand angle de champ pour sauvegarder le peu de pixels disponibles. Tel que prévu, le contraste de l'image est notablement réduit localement et une certaine proportion de la lumière est diffusée sur toute sa surface. En principe, il s'agit d'un défaut, mais comme c'est souvent le cas en photographie il arrive qu'on provoque délibérément des anomalies dans le but d'obtenir un effet spécial. Il suffit d'observer les images qu'on a obtenues à l'aide du sténopé pour se rendre compte qu'elles ne manquent pas de charme et de mystère. Un trou d'un millimètre de diamètre permet de réduire les défauts les plus graves, mais alors c'est la pseudo-focale et donc les dimensions de la caméra qui deviennent presque impraticables : environ 75 cm. La photographie électronique. En l'espace de quelques années, les matrices CCD (dispositifs à couplage de charge) ou CMOS électroniques ont complètement supplanté le film à sels d'argent. Il faudra attendre sans doute encore longtemps, mais cet événement révolutionnera un jour la manière d'aborder le sténopé. Non seulement le temps de pose qui constituait le handicap majeur du sténopé sera sensiblement réduit, mais les nouvelles surfaces photosensibles pourront être faites cylindriques sans trop d'inconvénients. On peut même prévoir qu'un jour, parce que c'est le champ sphérique qui ne produit aucune distorsion dès la prise de vue, elles pourront même être faites sphériques en respectant des méridiens et des parallèles déterminés par convention. Parce qu'il se forme une tache d'Airy dont les dimensions valent environ la moitié de celles du trou, le "sténopé électronique" se distinguera de la caméra électronique normale par ses matrices à pixels très grands, soit environ 0,25 mm. On réalisera bientôt, je l'espère, que cet appareil jouit d'un avantage considérable sur le film. En effet, plus la surface des photosites (les capteurs individuels) est grande, moins elle exige de lumière. Adieu le film ennuyeux qui exigeait des temps de pose interminables. Finies les contraintes. On peut enfin imaginer le sténopé en version électronique. Il sera nettement plus sensible à la lumière au point de permettre de prendre des instantanés, du moins en plein soleil. Malgré sa "lentille" rudimentaire, il sera capable de produire des photographies tout à fait remarquables, sous un très grand angle de champ et malgré tout sans aucune distorsion. Elles seront même si bonnes que ses plus ardents défenseurs le renieront peut-être, faute de mystère et de poésie. On montre plus loin que le sténopé présente de très nombreuses caractéristiques avantageuses, mais qu'il est imparfait. Dans le but d'en profiter tout en l'améliorant, on en arrivera finalement au concept du "sténopé à lentille". Le champ courbé. On enseigne en optique que la courbure de champ est une aberration. Au contraire, je montre à la page sur la courbure de champ que Petzval et Seidel ont fait erreur. Très clairement, ils se sont mis le doigt dans l'œil. Et je ne mâche pas mes mots. Le meilleur exemple est le sténopé montré ci-dessus. Il utilise un surface photosensible courbée, plus exactement cylindrique. Il existe de nombreuses variétés de projections cylindriques, la plus connue étant celle de de Mercator. Mais celle-ci n'apparaît pas sans distorsion si elle est observée sur un écran également cylindrique. Puisque les écrans s'étendent généralement en largeur et non pas en hauteur, la projection azimutale doit être maintenue sur les axes verticaux du cylindre, qui sont droits. Dans ce cas, le sténopé produit une image qui apparaît absolument sans distorsion pourvu qu'elle soit affichée sur un écran également cylindrique, même si on réalise un montage sur 360°. Autre avantage, la luminosité faiblit moins en périphérie. Le fait de l'afficher sur nos écrans plats actuels pose d'ailleurs moins de problèmes que si elle était obtenue à l'aide d'une caméra classique à champ plat. Les extrémités gauche et droite présenteront moins de distorsion, surtout si ces extrémités sont visionnées ou imprimées séparément. Il va de soi que ces images auront été réalisées sous un angle de champ relativement grand, car la petite pupille du sténopé est incompatible avec le champ étroit associé à la grande pupille d'entrée nécessaire aux téléobjectifs. En plus clair, un sténopé est obligatoirement une caméra à très grand angle. C'est là qu'il devient intéressant. Une formule délinquante. Le point important à retenir, car ce n'est pas ce que le sens commun donne à penser, c'est que plus la pupille est grande, plus l'image est précise. Le problème, c'est qu'il faut alors allonger la pseudo-focale (la distance entre la pupille et la surface photosensible) en conséquence. Alors la caméra nécessaire deviendrait gigantesque et la luminosité relative par pixel serait moindre, d'où un temps de pose excessivement long, voire impraticable à cause de l'effet Schwarzschild. On établit généralement la longueur d'onde moyenne selon lambda = 0,00055 mm d'après le vert lime. C'est la couleur médiane du spectre visible, que l'œil perçoit d'ailleurs le mieux. Selon le diamètre D de la pupille, la pseudo-focale F devrait s'établir selon : F = D 2 / (2,44 * lambda) Mais il y a un hic. La plupart des amateurs (et même la NASA!) préfèrent utiliser la formule de lord Rayleigh, qui donne selon moi une distance insuffisante. Il existe de nombreuses autres formules, établies le plus souvent par tâtonnement, mais elles ne sont guère crédibles. Pour que vous puissiez faire un choix judicieux, j'ai donc mis côte à côte les deux formules en conflit. La pseudo-focale F vaudrait : |
|
F = D 2 / 2,44 l |
F = D 2 / 3,61 l |
|
Selon moi. |
Selon lord Rayleigh. |
|
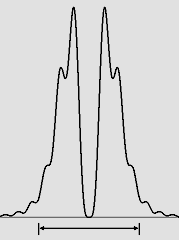
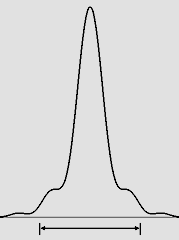
Pour autant que je sache, ma formule n'est proposée par personne et elle est donc "délinquante". Toutefois, les opticiens noteront qu'elle s'appuie sur le chiffre d'Airy. Ainsi une pupille de 1 mm exige une pseudo-focale de 745 mm, mais il faudrait 2,98 mètres si elle mesure 2 mm. C'est pourquoi un hurluberlu qui parviendrait à construire un sténopé de 3 mètres muni de photosites d'un millimètre chacun en tirerait des photographies spectaculaires. Mais ce serait bien inutilement, comme on le montre plus loin. À l'extrême limite du raisonnable, je propose dans cette page l'exemple suivant : D = 0,82 mm F = 500 mm Cette énorme caméra possédant une pseudo-focale d'un demi-mètre, elle permet en effet d'obtenir des images plus précises. Dans le but d'éliminer la distorsion, la surface photosensible doit bien sûr être cylindrique. Elle doit être aussi grande que possible, ce qui suggère environ 800 x 450 mm pour respecter le format 16 : 9. La limite de quatre pixels environ pour chaque tache d'Airy selon la limite de Dawes ou de Rayleigh n'est guère applicable dans le cas du sténopé puisque cette tache n'est pas encore formée. Les diagrammes montrés ci-dessous montrent toutefois qu'on s'en approche. De plus, le diamètre de la zone lumineuse centrale vaut environ le tiers de celui du trou du sténopé, ce qui donne à penser qu'on pourrait obtenir au maximum environ 2400 x 1350 pixels. On atteint donc alors confortablement les 1920 x 1080 pixels du format HDTV. La formule de lord Rayleigh donne une distance insuffisante (ci-dessous, 340 mm avec D = 0,82). Après mûre réflexion, il semble certain que ce choix était lié au fait qu'une distance plus grande exigeait un temps de pose plus long, voire impraticable. Sans aucun doute, le sténopé électronique sera moins assujetti à cette contrainte. Il tolérera une luminosité moindre au profit d'une meilleure résolution. L'ordinateur révèle que la distance de 500 mm proposée ici correspond au point où le diamètre de la tache d'Airy, encore en voie de formation, est égal au diamètre de la pupille (ici 0,82 mm). Bien évidemment, ce diamètre fait référence aux points où la luminosité atteint un minimum (qui n'est pas nul), car en pratique l'essentiel de l'énergie est concentré dans la moitié de ce diamètre. Il est très important de réduire le plus possible la perte de résolution attribuable au premier anneau. Pour toute distance inférieure, cet anneau est en effet beaucoup trop lumineux et il est encore nettement rattaché au lobe principal, comme le montrent les diagrammes ci-dessous : |
 |
 |
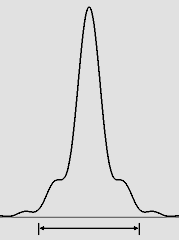 |
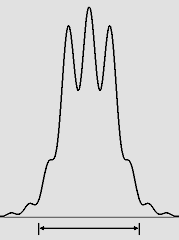
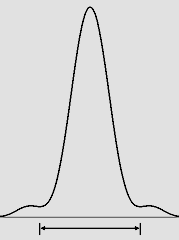
| D 2 / (8 * lambda) = 153 mm | D 2 / (6 * lambda) = 204 mm | D 2 / (4 * lambda) = 306 mm |
 |
 |
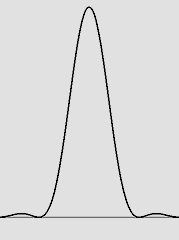 |
| D 2 / (3,61 * lambda) = 339 mm | D 2 / (2,44 * lambda) = 500 mm | Tache d'Airy idéale. |
Quelques diagrammes de rayonnement du sténopé ou du laser.
|
On notera que même à la distance jugée idéale, soit 500 mm, le premier anneau n'est pas encore tout à fait détaché du disque central. Il accapare encore beaucoup de lumière, ce qui nuit à la précision de l'image. Hélas, la tache Airy idéale ne se forme qu'à grande distance. Ce défaut est encore accentué si la source est placée à faible distance et non à l'infini, ce qui fait que le sténopé ne permet pas de faire des plans rapprochés aussi précis, par exemple des portraits. Mais d'un autre côté, il existe de nombreux photographes qui aiment le sténopé précisément parce qu'il produit cet effet de diffusion caractéristique. Dans ce cas, ils ont intérêt à choisir une distance encore plus courte que celle qui a été suggérée par Lord Rayleigh : F = D 2 / (4 * lambda) ...soit selon le nombre de Fresnel n = 1 : F = R 2 / lambda F = 306 mm. Cette distance sera alors doublement avantageuse car elle correspond au point n = 1 où la luminosité atteint un maximum. Il faudra donc beaucoup moins de lumière ou de temps pour réaliser un cliché et étonnamment, la précision de l'image demeure relativement bonne. Il convient de rappeler que même la distance de 500 mm suggérée dans cette page produit exactement la même diffraction, qui est considérable avec une pupille de 0,82 mm. Sur le diagramme ci-dessous, la distance de 306 mm correspond au trait gris vertical central, alors que la pseudo-focale de 500 mm suggérée correspond plutôt au trait vertical noir montré à droite. La largeur de la pupille est indiquée par les deux traits gris horizontaux. Il s'agit d'une vue longitudinale du faisceau lumineux qu'on obtient à l'aide d'un point lumineux très éloigné (une étoile réelle ou artificielle), le plan comprenant l'axe optique : |
|
|
L'évolution du faisceau lumineux : le trou du sténopé est situé à l'extrême gauche.
Pour plus de clarté, les proportions sont fortement comprimées dans le sens de la longueur.
La pseudo-focale idéale est indiquée par le trait vertical noir : L = D 2 / (2,44 * lambda) = 501 mm.
Le trait vertical gris le plus à droite indique le point de luminosité maximum : L = D 2 / (4 * lambda) = R 2 / lambda = 306 mm.
Le « point noir » le plus éloigné du trou apparaît à la distance L = D 2 / (8 * lambda) = R 2 / (2 * lambda) = 153 mm.
De droite à gauche, les traits gris correspondent à un nombre de Fresnel « n » entier allant de 1 à 7.
La formule de Fresnel considère plutôt le rayon R du trou : L = R 2 / (n * lambda)
|
|
À gauche, la tache d'Airy idéale. À droite, celle que produit le sténopé (D = 0,82) à 500 mm.
Ces diagrammes montrent l'amplitude, et non pas l'énergie qui vaut son carré.
Même à cette distance, le premier anneau n'est pas encore complètement détaché de la tache centrale.
De plus les autres anneaux sont encore trop lumineux, d'où l'effet de diffusion caractéristique du sténopé.
Très souvent, cet effet de diffusion est plus sévère encore parce le contour de la perforation est irrégulier.
|
Le nombre de Fresnel. On remarquera le fameux phénomène du "point noir" à 153 mm avec n = 2. Dans l'ensemble, la structure du faisceau correspond à la diffraction de Fresnel classique. Les photographes amateurs utilisent les formules qui privilégient le diamètre D du trou, mais Fresnel considérait plutôt le rayon R, avec raison puisque cela permet de simplifier. C'est ainsi qu'on parle du nombre de Fresnel, qui est l'entier n dans les équations suivantes, la grandeur L étant la distance de la pupille : L = D 2 / (4 n * lambda) L = R 2 / (n * lambda) D = 0,82 mm R = 0,41 mm Il y a d'autres points noirs plus près, car ils se produisent selon n = 2, 4, 6, ... fois la longueur d'onde, donc avec n pair. Lorsque n est impair, on obtient plutôt un point blanc, c'est à dire un maximum de luminosité. C'est ainsi que le premier point blanc avec un nombre de Fresnel n = 1 se produit à la distance de : L = D 2 / (4 * lambda) L = R 2 / lambda L = 0,41 2 / 0,00055 = 306 mm. Le point de luminosité maximum. Il convient donc de souligner qu'il existe une distance pour laquelle la luminosité de la tache d'Airy atteint un maximum. C'est très visible sur le diagramme longitudinal montré plus haut. Les photographes qui ont désespérément besoin de lumière la préféreront, mais ce n'est pourtant pas la distance idéale s'ils désirent obtenir la photographie la plus précise possible. Comme on l'a vu plus haut, il arrive que certains photographes recherchent délibérément cet effet ; mais un grand nombre de sténopistes se laissent berner par cette luminosité trompeuse, en tous cas s'ils ignorent que la précision de l'image en souffre. Cette distance correspond au point où toutes les ondelettes de Huygens et particulièrement celles provenant de la périphérie de l'ouverture plane cessent de se détruire comparativement à celles qui proviennent du centre. Selon Pythagore on peut vérifier que la différence entre la diagonale et la longueur L vaut alors une demi-longueur d'onde. Alors il n'y a plus du tout d'interférences destructives et l'on peut donc s'attendre à ce que la luminosité du disque central atteigne un maximum. Contrairement à ce que pensent beaucoup d'amateurs, ce n'est qu'au-delà de ce point que la règle du carré de la distance s'applique, du moins en première approximation. On peut aussi assimiler ce point au fameux critère de Rayleigh si cher aux astronomes amateurs qui polissent eux-mêmes les miroirs de leurs télescopes. Il s'agit en effet de faire en sorte que la période des ondelettes de Huygens ne dépasse jamais une demi-longueur d'onde de manière à ce qu'elles ne se détruisent jamais. On a alors un quart d'onde de dénivellation au maximum sur le miroir à cause de l'aller et retour, mais la tache d'Airy est alors quand même imparfaite pour la même raison. Un programme d'ordinateur simple et efficace. En parfait délinquant, j'ai inventé moi-même le petit programme qui a tracé ces courbes. Il ne fait qu'additionner le sinus et le cosinus de la différence de marche de milliers d'ondelettes fictives, convertie en période d'onde, conformément au principe de Huygens. Sa simplicité est remarquable. Ceux qui auraient des doutes peuvent télécharger un petit programme fait spécialement à leur intention. Le dossier .zip contient le programme QuickBasic en mode texte, le code source original et enfin un fichier exécutable .exe qui fonctionne sur tous les ordinateurs sauf Macintosh. On y montre comment quelques centaines de points en guise d'échantillons répartis sur une surface circulaire peuvent produire la courbe caractéristique de la tache d'Airy. Ceux qui connaissent la programmation pourront modifier la distance et constater que cette méthode fonctionne à merveille. Mes programmes actuels sont beaucoup plus rapides parce qu'ils calculent des arcs de cercle et non des points. Depuis l'apparition de FreeBASIC, j'ai considérablement amélioré ma méthode de calcul. Si ce n'est déjà fait vous pouvez télécharger ma suite complète sur l'éther : Le programme qui reproduit le faisceau lumineux du sténopé se nomme Ether15. J'ai même réussi à adapter cette méthode pour calculer la tache d'Airy idéale produite par une source concave : c'est le programme Ether16. Vous constaterez en examinant le code source que contrairement aux opticiens, je n'utilise pas le calcul différentiel traditionnel, qui fait souvent appel à la transformée de Fourier et à l'approximation de Fraunhofer. J'ai plutôt mis au point un algorithme basé sur le principe de Huygens. Le secret de sa grande rapidité, c'est qu'il met en oeuvre des arcs de cercle en nombre limité plutôt que des points en très grand nombre. Il suffit d'en faire la sommation selon le sinus et le cosinus de la distance convertie en période d'onde. À ce jour, aucun opticien n'a voulu admettre que cette méthode est intéressante (pourtant, elle est même géniale!), mais ça viendra. Tôt ou tard, le simple bon sens triomphera. Le laser est un "sténopé émetteur". Dans le domaine des ondes, tout système récepteur (par exemple une antenne) peut devenir un émetteur, ou inversement. De la même manière, le sténopé utilise une surface circulaire plane équiphasée, c'est à dire sa pupille, en tant que récepteur. Or le laser en tant qu'émetteur produit exactement les mêmes diagrammes, car sa surface émettrice circulaire plane est elle aussi équiphasée, du moins en principe. Puisque l'angle de divergence d'un laser correspond au chiffre d'Airy, il devient évident que c'est le point de jonction correspondant à l'égalité entre le diamètre de la fenêtre émettrice et celui du faisceau lumineux qui détermine le point où la résolution du sténopé plafonne. Voyons cela. Le point de jonction. Le diamètre de la tache lumineuse produite par un point lumineux très éloigné, par exemple une étoile, est égal au diamètre de la pupille si la distance (et donc la pseudo-focale F) correspond au chiffre d'Airy. Cette distance L va de la pupille à ce qu'on peut appeler le point de jonction : L = D 2 / (2,44 * lambda) L = 501 mm. En se référant à l'angle de divergence d'un laser, on trouve que c'est à cette distance que le diamètre de la tache d'Airy coïncide avec le diamètre de la source. Or le diamètre de la tache lumineuse n'est jamais inférieur, puisque le faisceau lumineux est cylindrique entre la pupille et le point de jonction.On en déduit que la précision de l'image produite par un sténopé augmente jusqu'au point de jonction. Par contre elle plafonne au-delà de ce point parce que le diamètre de la tache d'Airy se met alors à augmenter, soit selon l'angle de divergence d'un laser. Il mesure par exemple deux fois 0,82 mm et donc 1,64 mm si la distance vaut le double, soit un mètre. À mon avis le diagramme ci-dessous le montre d'une manière évidente : |
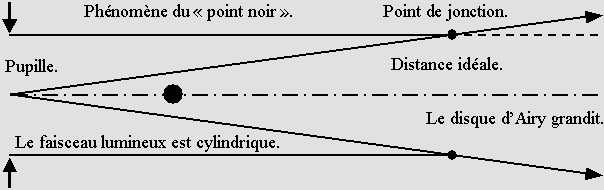
Le point de jonction représente le meilleur choix.
|
En conclusion. Considérant les possibilités étonnantes du sténopé, on se prend alors à regretter son manque de précision. Le contraste et la précision d'une image obtenue à l'aide du sténopé ne sont en aucun cas aussi bons que si la pupille est munie d'une lentille de bonne qualité. Le diagramme ci-dessous montre ce qu'on obtient avec une lentille véritable dont le diamètre et la focale seraient les mêmes que ceux du sténopé proposé ici, soit 0,82 mm et 500 mm. On a alors une ouverture relative très élevée de ƒ/ 610, mais il n'y a pas lieu de paniquer car elle permet de faire des miracles : |
|
|
L'ajout d'une lentille améliore le sténopé d'une manière dramatique.
Le trait vertical noir situé à droite indique l'emplacement précis du plan focal.
Ce n'est pas le point le plus lumineux, mais c'est le point où la tache d'Airy est enfin absolument parfaite.
Il convient de préciser que la diffraction demeure toutefois identique, car c'est bien ce qu'on recherche avec le sténopé.
|
Le sténopé présente des avantages sur les caméras conventionnelles, mais la tache d'Airy très imparfaite demeure un inconvénient majeur. La solution, c'est de lui ajouter une lentille de manière à obtenir une tache d'Airy pratiquement sans défauts malgré l'ouverture relative considérable. L'un n'empêche pas l'autre. Ce serait abusif d'affirmer qu'un sténopé n'est plus un sténopé s'il est muni d'une lentille car il conserve au contraire toutes ses propriétés fondamentales. L'ajout d'une lentille permettrait par exemple de régler la mise au point une fois pour toutes sur l'hyperfocale, soit la focale qui permet de concilier la profondeur de champ (qui on l'a vu est très grande) avec la distance la plus utilisée. Ceux qui ne font que des portraits pourraient ainsi mitrailler leur cible sans se soucier de la mise au point, avec la certitude que leurs images seront à coup sûr d'une précision cristalline. On remarque aussi sur le diagramme ci-dessus que l'emplacement précis du plan focal est difficilement identifiable. Il pourrait sans inconvénients se situer un peu plus près. Mais il pourrait surtout se situer beaucoup plus loin, et nous sommes ici en présence d'une caractéristique unique au sténopé à lentille. Observez bien le diagramme ci-dessous, qui est celui d'une tache d'Airy normale. C'est celle qu'une lentille ou un miroir de télescope produit. Vous remarquerez qu'elle est parfaitement symétrique. De chaque côté du plan focal se situe un "point noir" semblable à ceux qui sont montrés ci-dessus, mais d'autres suivent et tous sont régulièrement espacés au lieu de respecter le nombre de Fresnel.
La tache d'Airy normale, vue par le travers. On y trouve des "points noirs" régulièrement espacés de chaque côté du plan focal.
Personne ne semble avoir remarqué que pour une pupille donnée, si la focale d'une lentille est plus grande ou égale à la pseudo-focale du sténopé, les points noirs situés au-delà du foyer sont absents. En pratique, le plan focal se prolonge donc indéfiniment. Il s'agit d'une propriété unique qu'on peut avantageusement mettre à profit en ayant recours à une surface photosensible cylindrique. Dans ce cas, la tache d'Airy est intacte partout sous réserve qu'elle est un peu plus grande et un peu moins lumineuse si elle se forme plus loin. Sur un plan horizontal, la focale peut se situer exactement au foyer idéal, qui est sphérique. Mais sur un plan vertical, la surface photosensible est droite. Le haut et le bas doivent donc se situer plus loin que le foyer idéal, mais comme on vient de le voir la tache d'Airy est à peine un peu plus grande et moins lumineuse. Elle et ses anneaux demeurent toutefois intacts et ce n'est donc pas très grave. Après mûre réflexion, on en arrive alors au concept délinquant du "sténopé à lentille". |
![]()
LES STÉNOPÉS À LENTILLE
|
Cette expression semble contradictoire puisque le sténopé est précisément une caméra sans lentille. Mais en réalité le sténopé se distingue d'une caméra conventionnelle sous de nombreux aspects :
Le sténopé représente donc de toute évidence la caméra grand angle idéale. Or l'ajout d'une lentille fixe très faible lui conserve ces avantages tout en améliorant la qualité de ses images. On peut même ajuster la mise au point pour de bon sur l'hyperfocale, ce qui augmente grandement sa précision à courte distance. Les caméras électroniques mesurent automatiquement le temps de pose et la luminosité selon certaines préférences. Finalement, il suffira d'appuyer sur le bouton pour obtenir une photographie remarquable. Ce n'est pas nécessairement ce que souhaitent les photographes chevronnés, mais c'est ce que souhaitent la plupart des gens. On peut encore espérer que le rendement de ces caméras sous un faible éclairage s'améliore quelque peu dans l'avenir. Alors une pupille d'entrée de 1,5 mm seulement permettrait de réaliser d'excellentes photographies sans allonger indûment le temps de pose. Le cinéma aussi est devenu électronique et il semble vouloir privilégier le format 16 : 9 déjà adopté pour la télévision. On parle même de super-haute définition et d'ultra-haute définition (33 mégapixels !). On aurait tout intérêt à adopter le champ cylindrique pour les prises de vue. Les écrans aussi devraient idéalement être cylindriques mais ce n'est pas vraiment nécessaire. Pour qu'il puisse observer une image qui lui apparaîtra absolument exempte de distorsion, le spectateur doit se situer au centre de courbure et au niveau du centre de l'écran. Une pupille de 1,5 à 2 mm. C'est un rêve illusoire, mais supposons que les manufacturiers arrivent un jour à produire des caméras électroniques mille fois plus sensibles à la lumière. Dans ce cas, les photographes seraient libérés de l'obligation d'avoir à ouvrir leur lentille d'une manière excessive. Il y a deux raisons à ça. En règle générale (mais pas toujours) ils souhaitent obtenir la plus grande profondeur de champ possible. De plus, on sait que la précision des lentilles photographiques diminue de manière radicale à grande ouverture, surtout dans le cas des lentilles grand angle. Pour vous en convaincre, vous n'avez qu'à calculer leur résolution à partir de la bague de profondeur de champ. Vous trouverez probablement des valeurs entre 0,05 et 0,075 mm pour le cercle de moindre confusion alors que la tache d'Airy à ƒ/ 2 fait moins de 0,003 mm. Cela signifie que l'image pourrait être 25 fois plus précise si la lentille était parfaite ! Le calcul montre que pour atteindre un résultat tout juste acceptable, les fabricants devraient privilégier une pupille d'environ 1,5 à 2 mm sur leurs caméras grand angle. Ce diamètre dépend en effet de l'angle de champ de la caméra comparé au nombre de pixels qu'ils souhaitent obtenir. Le calcul est relativement simple : il suffit de mesurer la surface de l'image utilisable sur le plan focal et de voir combien elle peut contenir de taches d'Airy en appliquant la limite de Dawes. Voyons donc ces pixels. Entre 2 et 6 mégapixels. La tendance actuelle pour les images numériques semble se stabiliser à moins de 10 mégapixels, ce qui permet par exemple de produire une image qui remplit très facilement l'écran d'un téléviseur à haute définition (1080 x 1920 = 2 mégapixels). On peut aussi raisonnablement croire (ou espérer) que les écrans des ordinateurs deviendront plus précis. Je possède moi-même un moniteur faisant 1920 x 1200 pixels et je ne pourrais plus revenir à mon ancien 1280 x 1024. En fait, je n'arrive pas à croire que la plupart des gens dépensent une fortune pour se procurer des ordinateurs portables ou des téléphones dont la résolution est misérable en comparaison. Je tiens aussi à souligner qu'on met beaucoup de temps à offrir des caméras numériques à deux objectifs capables de réaliser des prises de vue en trois dimensions. Après tout, les écrans HDTV offrant la 3-D sont déjà disponibles. De plus, il est évident que les gens voudront de plus en plus visionner leurs photographies sur leur téléviseur ou sur leur ordinateur, les images imprimées devenant moins intéressantes à cause de leur faible contraste. Si tout se passe de cette manière, la projection cylindrique sera nettement avantagée, et les deux appareils montrés ci-dessous pourraient devenir populaires à cause de leur simplicité, leur précision sans reproche et leur profondeur de champ exceptionnelle. Voici donc deux modèles de sténopés à lentille parmi d'autres que j'ai proposés : |
![]()
|
|
Le sténopé à lentille double ménisque.
|
La lentille double ménisque est achromatique parce que l'effet de prisme du premier élément est annulé par le deuxième. Elle est pratiquement exempte de coma et d'astigmatisme à une telle ouverture à cause de sa structure pratiquement concentrique. Ainsi la tache d'Airy demeure parfaite quel que soit l'angle de champ, qui peut atteindre facilement et même dépasser 90°. Certaines caméras à champ cylindrique du début du 20e siècle étaient construites un peu de cette manière mais leurs performances étaient décevantes à cause du film peu précis et peu sensible. Il s'agit bel et bien d'un sténopé à lentille, car il faudrait adopter une ouverture relative d'environ ƒ/ 50 ou plus, dépendant de l'angle de champ vertical. La partie ombrée montre les zones où la mise au point est bonne. On peut constater que même si la surface photosensible apparaît droite en élévation, elle demeure à l'intérieur de cette zone. Sur un plan horizontal cette surface est cylindrique de manière à coïncider avec les pointillés, qui correspondent à l'hyperfocale. Une pupille d'entrée dont le diamètre fait un seul millimètre peut tout juste satisfaire les exigences d'un écran HDTV. La focale ne serait que de 50 mm à ƒ/ 50. On peut obtenir facilement 6 mégapixels sur 90° avec une pupille de 2 mm, mais la focale devrait plutôt être de 200 mm à ƒ/ 100 pour un même angle de champ vertical. La profondeur de champ serait à peine réduite. La caméra serait relativement encombrante et même énorme mais en tous cas elle serait très légère. Les professionnels et les amateurs avertis apprécieraient certainement que le dos d'une si grande caméra soit équipé d'un grand écran à haute définition qui permettrait de mieux visionner les images. Pourquoi s'en priver ? Impossible de faire de meilleures images. On peut penser que même dans un avenir éloigné, il ne sera jamais possible d'obtenir de meilleures images, à des poussières près. Il sera par contre très possible d'obtenir les mêmes images à l'aide de la lentille « Oeil d'aigle » montrée à la page sur la courbure de champ. Dans ce cas les caméras pourront être vraiment minuscules, leurs dimensions étant réduites à aussi peu qu'un centimètre ou deux.. Toutefois mes plus récentes analyses de la tache d'Airy montrent qu'il faudra éviter les ouvertures relatives de ƒ/ 1 ou moins. En effet, et bien que ceci ne soit guère souligné par les opticiens, tout indique qu'elles conduisent à une perte de contraste parce que la luminosité relative des anneaux augmente alors d'une manière catastrophique. De toutes façons, en lumière normale, les dimensions des photosites électroniques actuels ne peuvent guère descendre sous le seuil des 0,01 mm. Un gaz lourd comprimé ? Mon ouvrage Optique des miroirs proposait de faire les ménisques parfaitement concentriques et de les remplir d'un gaz comprimé. En effet la bulle de gaz agit comme une lentille convergente, mais surtout elle le fait uniformément quel que soit l'axe considéré. À cause du nombre d'Avogadro, un gaz lourd est préférable car il permet de limiter la pression. Une telle lentille serait exempte de toute aberration. On pourrait même ajuster la mise au point en variant la pression. Le seul point que je n'ai pas encore éclairci concerne l'indice de dispersion d'un tel gaz, que je n'arrive pas à connaître, et qui pourrait se révéler incompatible avec celui du verre des ménisques. À pression plus faible ce système pourrait aussi servir de correcteur d'aberration de sphéricité dans un télescope de Schmidt à miroir sphérique. C'est l'équivalent d'un correcteur de type ménisque concentrique, soit la version de son inventeur Bouwers et non pas celle de Maksutov. Le gaz comprimé a pour effet d'annuler l'effet divergent du ménisque, ce qui annule l'aberration chromatique. Mais l'immense avantage de ce système, c'est qu'il fonctionne parfaitement quel que soit l'angle de champ parce que tous ses éléments incluant le miroir sont sphériques et concentriques. C'est donc le Schmidt ultime. À moins que quelqu'un n'ait revendiqué cette idée, je prétends que c'est l'une de mes nombreuses inventions. Elle n'est pas brevetée mais elle figure dans mon livre disponible ci-dessus, qui est protégé par un droit d'auteur. Ci-dessous, voici la caméra "Mercator" : |
![]()
|
|
La caméra « Mercator ».
|
Peu de gens savent que le cristallin de l'œil agit très peu en tant que lentille. Il agit surtout en modifiant le rayon de courbure de la cornée, qui est convexe. Par exemple, une simple bille de verre optique parfaitement sphérique agit comme une lentille pourvu que son centre soit muni d'une pupille. On peut mettre à profit ce principe en construisant une petite caméra tout à fait remarquable faite d'un seul bloc de plastique léger (un modèle plus grand serait trop lourd). Il faudrait plus exactement coller deux éléments de plastique transparent de chaque côté d'un iris de 1 mm, qui se trouverait scellé définitivement à l'intérieur. La face avant doit être convexe et la face arrière, cylindrique. De cette manière la lumière converge dès qu'elle pénètre dans la lentille. Elle n'en sort plus, la surface photosensible électronique étant collée (et bien protégée) sur la face cylindrique. Même si la pupille est scellée dans la matière plastique, je présume qu'il est possible d'inventer un diaphragme à cristaux liquides inséré dans la pupille. Un diaphragme peut en effet se révéler très utile au besoin. L'aberration chromatique n'est pas nuisible avec une pupille aussi petite. À cause de la structure concentrique il n'y a pas de coma ni d'astigmatisme. Ainsi la tache d'Airy demeure intacte quel que soit l'angle de champ. Pour le reste le fonctionnement de cet appareil est identique à celui du précédent. Cet appareil pourrait être une autre de mes inventions, mais parce que ce concept est très simple, je ne gagerais pas là-dessus. D'ailleurs des tas d'inventions ne sont pas connues. La plupart ne sont ni brevetées ni utilisées. Beaucoup sont disparues, oubliées, et les autres dorment simplement sur des tablettes, quelque part. Malheureusement, j'ai pu vérifier que les brevets d'invention n'étaient qu'une taxe sur l'imagination, d'ailleurs h orriblement chère. Ils ne profitent que rarement à leur auteur. |
![]()
L'APODISATION
|
La pupille de 1,5 ou 2 mm pourrait être portée à 3 ou 4 mm à la condition de l'apodiser. Ce terme signifie qu'elle devrait être munie d'un filtre qui élimine progressivement la lumière en périphérie, idéalement selon la courbe bien connue en forme de cloche, appelée distribution normale ou gaussienne. La formule approchée de cette courbe est indiquée ci-dessous, mais le chiffre pi n'est pas pertinent ici. Il faut savoir que c'est le mathématicien Denis Poisson qui fut à l'origine de cette distribution dite de Gauss-Laplace. Le filtre produirait un disque lumineux sans les anneaux (voir plus bas), lui aussi réparti en lumière selon la distribution normale. Tout indique que la qualité des images en serait améliorée. Mon programme montre qu'on peut obtenir un effet comparable en réduisant plutôt la lumière selon un triangle isocèle amputé horizontalement de sa pointe supérieure et verticalement de ses deux pointes inférieures. |

|
S'il y a des anneaux, le disque central ne contient que 83,78 % de la lumière. L'apodisation a pour effet de récupérer toute la lumière manquante, mais le disque obtenu est alors plus grand. C'est pourquoi il faut doubler ou même tripler le diamètre de la pupille pour compenser. C'est impraticable dans le cas des télescopes, non seulement parce que leur diamètre devrait être considérable, mais aussi parce que la présence d'une obstruction centrale s'il s'agit d'un télescope à miroir est alors encore plus dommageable. Elle est tout aussi impraticable s'il y a un diaphragme à iris. C'est pourquoi tous les textes consultés déconseillent cette méthode. On a fait de nombreuses études à ce sujet, mais le cas des sténopés à lentille est très particulier. Mes analyses indiquent qu'on est ici en présence d'une exception. En effet, la pupille est très petite, sans diaphragme et sans obstruction. Alors le fait d'accroître son diamètre et de l'apodiser ne devrait pas poser de problèmes. On montre ci-dessous la différence entre une tache d'Airy normale et un "disque de Poisson". |
|
|
|
À gauche, la tache d'Airy entourée d'anneaux.
À droite, le « disque de Poisson ».
|
Ainsi, les anneaux étant absents, non seulement la précision et le contraste de l'image devraient en être améliorés, mais rien n'indique que la profondeur de champ (qui on l'a vu atteint un maximum) devrait en souffrir. On peut facilement l'expliquer en montrant que si elle est répartie selon ce qu'il est convenu d'appeler le disque de Poisson, la plus grande partie de la lumière s'en trouve concentrée beaucoup plus près de l'axe du faisceau lumineux. Certains diront que le jeu n'en vaut pas la chandelle, mais ça reste à vérifier. Par exemple, toutes les lentilles de bonne qualité sont recouvertes d'un antireflet. Si l'apodisation procure un gain comparable, on l'adoptera certainement un jour. Elle a d'ailleurs un autre avantage : si l'image est hors foyer, les anneaux demeurent absents. La lumière n'est jamais dispersée au-delà du disque lui-même, dont les dimensions augmentent toutefois, bien évidemment. Or sans apodisation, ce sont aussi les nombreux anneaux, dont certains sont très loin du disque, qui s'en trouvent accentués. Alors non seulement l'image est plus floue, mais à cause de l'effet de diffusion son contraste en est beaucoup plus affecté localement. Il se peut que je me trompe à ce sujet car je n'ai pas les moyens techniques de le vérifier. Une erreur volontaire. L'Internet montre qu'il existe de très nombreux adeptes du sténopé. On aura beau leur dire que les caméras électroniques font des images plus précises, ils continuent de se passionner pour cette caméra étrange. Et le pire, c'est qu'ils ont raison. |
|
Gabriel LaFrenière, Bois-des-Filion en Québec. Sur l'Internet depuis septembre 2002. Dernière mise à jour le 24 octobre 2009. Page d'accueil : La matière est faite d'ondes. Courrier électronique : veuillez consulter cet avis. La théorie de l'Absolu, © Luc Lafrenière, mai 2000. La matière est faite d'ondes, © Gabriel Lafrenière, juin 2002. Optique des miroirs, © Gabriel Lafrenière, juillet 2001. ISBN 2-9806972-2-2 |