
LA TACHE D'AIRY (page 2)
![]()
![]() Page d'accueil : La matière est faite
d'ondes.
Page d'accueil : La matière est faite
d'ondes.
L'OBSTRUCTION DES TÉLESCOPES À MIROIR
|
On sait que la plupart des télescopes à miroir, le plus souvent de type Newton et Cassegrain, font appel à un miroir secondaire qui doit être placé en plein centre du faisceau lumineux convergent. Cette façon de faire a pour effet de déporter une partie de la luminosité du disque central vers les anneaux qui l'entourent. Le contraste et la précision de l'image en sont d'autant plus affectés que l'obstruction est importante. Tout ceci est bien connu. En général, on s'entend pour dire qu'une obstruction de 20 % ou moins en diamètre est peu dommageable, mais les dégâts sont très perceptibles si elle atteint 33 %. Ils sont encore plus graves avec une obstruction de 50 %. Ci-dessous, on a superposé trois courbes selon 0 %, 33 % et 50 %. Puisque le premier anneau occupe une surface plus grande que le lobe central, il disperse beaucoup plus de lumière que ne le montrent les courbes : |
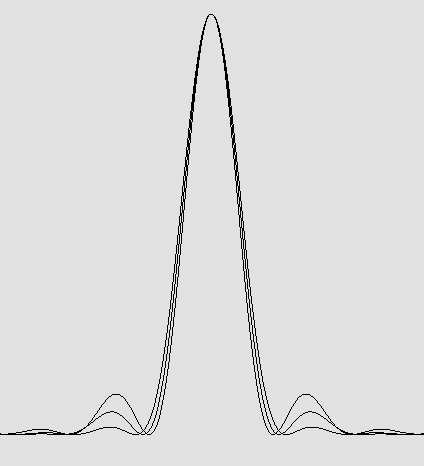
Les anneaux de la tache d'Airy deviennent plus lumineux si le centre du faisceau est obstrué.
|
L'obstruction n'est pas nécessairement nuisible. On pourrait en tirer un principe voulant qu'une obstruction de 50 % en diamètre doit être évitée à tout prix. Mais s'il est une chose que j'ai apprise à mes dépens, c'est qu'il faut se méfier des principes. Comme c'est le cas de toutes les balises, il arrive qu'ils aient été mal établis. Autrefois par exemple, la pellicule photographique n'arrivait pas à distinguer des détails inférieurs à 0,025 mm et c'est pourquoi un appareil ƒ/9 ou moins produisant une tache d'Airy de 0,012 mm au maximum se révélait incapable de distinguer la tache centrale du premier anneau. On comprend alors que les aberrations et les effets de l'obstruction étaient beaucoup moins perceptibles. Mais aujourd'hui, les caméras électroniques deviennent de plus en plus précises et les anciens Schmidt-Cassegrain peu précis et à forte obstruction risquent donc de révéler finalement leurs défauts cachés. Les nombreux astronomes amateurs qui possèdent un Schmidt-Cassegrain compact (33 % d'obstruction et parfois plus) se sont fiés à la publicité du manufacturier, qui est trompeuse parce qu'elle affirme que l'appareil respecte la tache d'Airy. Non seulement c'est inexact, mais le correcteur très puissant (l'appareil étant le plus souvent très compact) produit d'autres aberrations, surtout en périphérie de l'image. Depuis l'avènement des images numériques, ils doivent certainement remarquer le problème. D'un autre côté une obstruction plus grande permet d'obtenir des images plus grandes et donc d'enregistrer plus de pixels, ce qui permet de réaliser d'excellentes photographies de paysages, par exemple, à la condition que le système électronique capte tous ces pixels. En définitive, on peut dans certains cas obtenir d'excellentes images malgré la présence d'une obstruction considérable. Toutefois un Schmidt-Cassegrain compact ne permet certainement pas de réaliser des images aussi précises de la lune ou des anneaux de Saturne que le Newton ƒ/ 8 à faible obstruction équivalent, par exemple. Le télescope à miroir délinquant. Il existe une autre situation (exceptionnelle) où une telle obstruction est même avantageuse. Il s'agit de faire en sorte que la dénivellation sur le miroir du télescope ne dépasse pas un quart d'onde, de manière à éviter que certains rayons de lumière ne se retrouvent en opposition de phase à cause de l'aller et retour. En effet, les astronomes amateurs qui polissent des miroirs de télescopes savent bien qu'ils doivent respecter ce qu'ils appellent le critère de Rayleigh. C'est pourquoi un miroir de télescope est généralement paraboloïde, car au delà d'un certain diamètre, un miroir sphérique présente justement plus d'un quart d'onde de dénivellation comparativement à la parabole. Or cette dénivellation diminue à mesure qu'on augmente l'ouverture relative ou qu'on diminue le diamètre du miroir. De plus une obstruction centrale permet d'éliminer la zone centrale, qui excède la limite alors que tout le reste du miroir continue de respecter le critère de Rayleigh. Dans ces conditions l'obstruction agit comme un correcteur d'aberration de sphéricité. Bien évidemment, le fait de masquer le centre du miroir produira une tache d'Airy quelque peu dégradée, comme on l'a montré ci-dessus. Cependant, et c'est vraiment surprenant, un miroir sphérique ainsi corrigé produit des résultats bien supérieurs dans l'ensemble à ceux d'un miroir était parabolique. Le tout est d'avoir recours à la pupille de Schmidt, ce qui permet d'éliminer la coma et l'astigmatisme typiques du télescope de Newton, qui on le sait sont catastrophiques. Le Schmidt sans correcteur. Dans cette « optique », il existe un télescope peu connu nommé « Schmidt sans correcteur ». S'il est configuré avec soin, non seulement cet appareil produit peu d'aberration de sphéricité, mais il est également tout à fait exempt de coma et d'astigmatisme. Or ce n'est pas le cas d'un Newton, dont la précision loin de l'axe optique est vraiment désastreuse. Finalement, il est en mesure de produire des images beaucoup plus précises que le Newton parabolique équivalent, et sur une surface considérable. Le calcul montre par exemple qu'avec une telle obstruction, un petit miroir sphérique de 150 mm à focale d'un mètre seulement (ƒ/ 6,7) produit une image moins précise, mais dont l'étendue est considérable. En effet, une obstruction de 75 mm (soit 50%) permettait de remplir presque toute la surface de l'ancienne pellicule 6 cm x 6 cm, ce qui représente environ 4 mégapixels. En pratique ce n'est pas possible parce que le champ est courbé (son rayon de courbure vaut aussi un mètre). Mais puisque la photographie est désormais électronique, on pourra un jour utiliser des surfaces photosensibles courbées, et le tour sera joué. Un modèle plus grand mesurerait 2 mètres et atteindrait facilement 10 mégapixels. Il serait trop encombrant. Mais un bon bricoleur pourrait construire le modèle montrée ci-dessous, qui requiert un miroir sphérique facile à polir et un miroir plan perforé. Ce dernier doit être absolument plan dans le but de respecter là aussi le critère de Rayleigh ou à tout le moins d'éviter qu'il ne provoque de l'astigmatisme. On y arrive en alternant le polissage avec trois disques, selon la séquence 1-2, 1-3, 2-3, ce qui permet d'obtenir finalement trois miroirs plans. Au cas où vous ne l'auriez pas compris : NE FAITES PAS ÇA. Il n'existe pas encore de caméras électroniques à champ courbé sur le marché, et de toutes façons il est possible de faire mieux autrement. Dans le contexte de la délinquance, il s'agit ici de montrer que certains principes peuvent parfois être transgressés. Il vaut souvent mieux se fier à son intelligence, à la condition expresse d'en douter systématiquement et donc de tout vérifier. Chaque problème a sa solution, et ce n'est pas nécessairement celle qu'on trouve sur le marché. Le Schmidt-Porter avec ou sans correcteur. On sait que la pupille d'entrée du télescope de Schmidt doit être située au centre de courbure du miroir, c'est à dire deux fois plus loin que le plan focal. Même s'il n'est pas muni d'un correcteur de Schmidt, un tel télescope demeure un "Schmidt". Malheureusement, avec ou sans correcteur, ce télescope devient ainsi deux fois plus long qu'un Newton ou un Cassegrain. De plus, l'image qui se forme au foyer est sphérique. Son rayon de courbure étant égal à la focale, qui est généralement très courte, cet appareil est inutilisable avec les caméras numériques habituelles. Le miroir secondaire du Schmidt-Cassegrain peut cependant corriger cette courbure de champ. Afin de réduire la longueur du "Schmidt sans correcteur", il demeure possible de replier le chemin des rayons lumineux à l'aide d'un miroir plan perforé, ce qui permet de fabriquer un modèle moins encombrant que le Schmidt classique. À défaut d'en connaître l'inventeur, ce modèle étant peu connu, je l'ai appelé le Schmidt-Porter en hommage à Russell W. Porter, le créateur génial d'un télescope à tourelle utilisant un miroir perforé similaire. Il avait été construit à Stellafane, Vt, USA. On a réalisé des modèles plus grands par la suite. Voici donc ci-dessous la représentation de ce « Schmidt-Porter sans correcteur ». Il faut souligner que c'est surtout à cause de sa faible obstruction que ce télescope est intéressant. On remarque en effet que le foyer se forme très près de la perforation pratiquée dans le miroir plan et que le taux d'obstruction devient pratiquement négligeable si les miroirs sont relativement grands (disons 300 mm ou plus). Dans un Newton, au contraire, il faut allonger la distance qui va du secondaire au foyer. Un tel appareil muni d'un véritable correcteur de Schmidt serait beaucoup plus compact et il produirait des images (courbées) d'une très grande qualité. Il est donc en principe nettement supérieur au Schmidt-Cassegrain, le correcteur étant à sa place attitrée (répétons que la pupille de Schmidt se situe au centre de courbure du miroir) et l'obstruction étant négligeable.
|
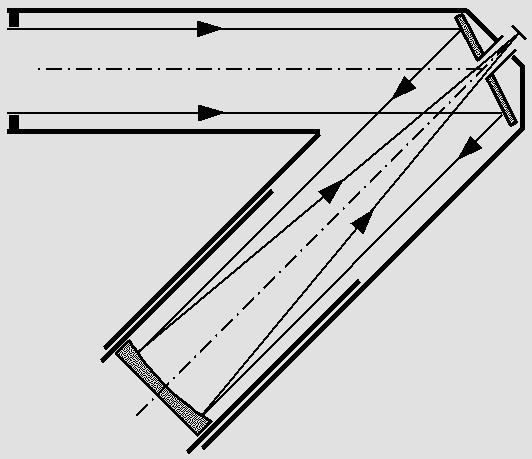
Le Schmidt-Porter sans correcteur.
Le miroir est sphérique, donc facile à polir en plus d'être plus précis.
Plus l'appareil est grand, plus l'obstruction est faible.
La pupille de Schmidt corrige à la fois la coma et l'astigmatisme de sorte que la précision de l'image est la même partout.
Il ne subsiste que l'aberration de sphéricité, qui est d'autant plus faible que l'appareil est long.
Il faut recourir à un correcteur de Schmidt pour éliminer ce problème, ce qui permet de raccourcir l'ensemble.
La courbure de champ traitée correctement n'est pas un inconvénient, bien au contraire.
LE CORRECTEUR DE PHASE
|
On a vu plus haut que l'obstruction centrale d'un télescope pouvait être utilisée pour masquer la zone centrale du miroir, si elle présente une dénivellation d'un quart d'onde sur la parabole qui se traduit par de la lumière en opposition de phase. Cette obstruction agit donc comme un correcteur d'aberration de sphéricité, ce qui permet de prévoir que si le miroir était plus grand, il faudrait ajouter des masques en forme de couronnes concentriques pour éliminer la lumière provenant des zones en opposition de phase. Le masque complet aurait un structure très semblable à celle de la lentille diffractive ou « zonale » selon le terme anglais zone plate, qu'il ne faut pas la confondre avec la lentille de Fresnel. Les zones sombres ou claires (au choix) montrées ci-dessous représentent les masques qui éliminent la lumière en opposition de phase, de telle sorte que la lentille diffractive fonctionne même avec des rayons X : |

La lentille diffractive ou « zonale ».
|
Toutefois, un tel correcteur calqué sur la lentille diffractive agirait effectivement comme une lentille, ce qui produirait de l'aberration chromatique. Pour éliminer l'effet uniquement convergent, Bernard Schmidt avait recommandé d'établir une zone neutre à 86,6 % du rayon du miroir de manière à distribuer équitablement la correction de part et d'autre. Supposons par exemple qu'on possède un miroir sphérique 200 mm ƒ/ 4. On peut calculer la focale effective (800 - 0,858 mm) de manière à n'utiliser que deux couronnes de part et d'autre de la zone neutre. Celle-ci se retrouve alors à environ 75 % du rayon. Ceci donne le masque suivant, dont la zone centrale représente l'obstruction du miroir secondaire : |
|
|
Le correcteur de phase.
|
Aucun des sites que j'ai consultés ne mentionne que les parties masquées de la lentille diffractive peuvent être remplacées par une épaisseur additionnelle sur une lame de verre, de manière à restituer à la lumière fautive la demi-onde manquante. Alors la lentille et le correcteur de phase seraient plus lumineux car ils utiliseraient toute la lumière. Mieux encore, ils seraient plus précis en réduisant les effets de diffraction, qui autrement sont catastrophiques. Il se pourrait que j'aie été le premier autrefois à décrire ces deux systèmes à transparence intégrale, mais vu leur simplicité je suppose que c'est très improbable. Ce correcteur de phase et l'une de mes inventions. Je n'ai jamais fabriqué de prototype et je n'ai donc pas vérifié ses performances. Beaucoup plus facile à fabriquer, donc moins coûteux, il pourrait remplacer le correcteur de Schmidt dans certaines situations moins exigeantes. Mon programme montre qu'il devrait produire une tache d'Airy un peu amochée mais tout de même acceptable. Toutefois, en pratique, les dénivellations entre zones pourraient le détériorer davantage ou diffuser de la lumière.
LES FENTES LUMINEUSES Une fente lumineuse produit sensiblement le même diagramme qu'une ouverture circulaire, mais on constate que les lobes sont nettement plus accentués. De plus l'ouverture étant plane et équiphasée, elle est comparable au diagramme d'un laser et non à celui d'une lentille. On observe là aussi qu'à courte distance le premier lobe n'est pas tout à fait détaché du lobe principal. Il faut observer les variations de phases attentivement pour comprendre que c'est parce qu'elles effectuent une rotation au lieu d'alterner simplement, comme c'est le cas avec la tache d'Airy normale. On remarque par la même occasion que le centre du lobe principal présente une avance de phase d'un huitième d'onde, comme on le verra plus loin. On montre ci-dessous, selon l'amplitude, la figure de diffraction que produit une fente lumineuse, à la condition qu'elle soit beaucoup plus longue que large. La distance de l'écran est de 4 mètres, et la largeur de la fente, 1 mm :
|
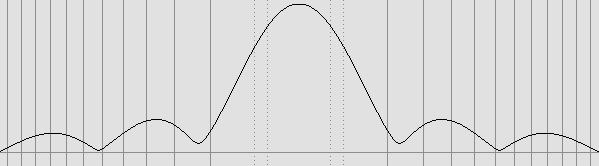
L'amplitude de la figure de diffraction produite sur un écran situé à 4 mètres de distance par une fente lumineuse de 1 mm de largeur.
|
Les lignes verticales indiquent les endroits où la période a effectué une rotation complète. Les deux premières lignes en pointillés indiquent le huitième et le quart d'onde. Peu d'auteurs prennent la peine de signaler ces faits parce qu'ils sont sans conséquences normalement. On verra maintenant qu'ils sont au contraire déterminants quand vient le temps de montrer ce qui se passe dans le cas où la fente lumineuse est remplacée par une obstruction identique. On peut par exemple imaginer un fil de fer dont la section vaut 1 mm, et qui est éclairé par un laser suffisamment éloigné pour produire une grande tache d'Airy plane ou presque plane. Si votre laser ne produit pas une tache d'Airy convenable à grande distance, vous pouvez diriger d'abord son faisceau vers une ouverture circulaire de 5 mm environ pratiquée dans un écran opaque. Celle-ci rayonnera par la suite un faisceau lumineux selon la diffraction de Fresnel-Fraunhofer et donc, à grande distance, une tache d'Airy parfaite avec ses anneaux typiques.
L'OMBRE D'UN FIL DE FER Pour les fins de cette démonstration, nous allons donc évaluer à quoi devrait ressembler l'ombre d'une obstruction relativement longue mais très étroite. Ce sera par exemple un fil de fer de 1 mm de section éclairé par un laser très éloigné. De la même manière que ci-dessus, l'écran sera placé à 4 mètres. Il s'agit de démontrer ici que la lumière traverse les objets sans rencontrer le moindre obstacle. Puisque la matière est faite uniquement d'électrons, ceux-ci étant faits d'ondes stationnaires, elle est tout à fait incapable d'arrêter la lumière. Par contre, les électrons réagiront à cette lumière en émettant des ondelettes sphériques produisant de la lumière en opposition de phase, ce qui justifie finalement l'ombre qui se produit derrière l'écran. Dans ces conditions, on peut s'attendre à ce que le fil de fer produise pour sa part exactement le même diagramme que la fente lumineuse, tel que montré plus haut. C'est une application du principe de Huygens. Mais d'autre part on peut s'attendre aussi à ce que toute la lumière qui provient du laser atteigne l'écran, même derrière le fil. Elle s'ajoutera donc à celle provenant du fil de fer. On en conclut qu'il devra se produire alternativement des interférences constructives et destructives selon la distance de l'axe. Ici, le fil de ver est disposé verticalement et cet axe est donc lui aussi vertical. |
|
|
L'ombre d'un fil de fer de 1 mm de section, à une distance de 4 mètres.
|
Rappelons ce qui a été souligné plus haut : le centre du lobe principal est en avance d'un huitième d'onde. Pour cette raison l'opposition de phase ne se produira que vis à vis le premier repère vertical, ce qui fait que le centre de l'ombre ne sera pas tout à fait noir. Par la suite, on constate que l'amplitude oscille entre un minimum et un maximum à l'intérieur du gabarit tracé en rouge. Ce gabarit reproduit bien évidemment le diagramme de la fente lumineuse équivalente montré plus haut. La lumière traverse les objets. Cette démonstration est on ne peut plus claire. Elle indique d'une manière convaincante que la lumière traverse les objets, et que les photons n'existent pas. Elle lève une objection fondamentale que les plus futés auraient pu opposer à mon hypothèse voulant que la matière soit faite d'ondes. Il leur faudra trouver d'autres objections. Il est intéressant de noter que le centre de la tache d'Airy d'un laser est en avance d'un quart d'onde (et non pas d'un huitième d'onde) à une distance équivalente, sa formation étant encore incomplète. C'est pourquoi le centre de l'ombre d'une obstruction circulaire est nettement plus éclairé. En fait, comme l'avait prévu Denis Poisson, « le centre de l'ombre d'un écran est aussi éclairé qu'en l'absence d'un écran ». Plutôt que de recourir à un écran circulaire difficile à tailler et à maintenir en place, vous pouvez vérifier ce phénomène plus facilement en déposant une petite goutte d'huile bien ronde sur un miroir plan optique et en éclairant le tout avec un laser éloigné (à nettoyer ensuite avec la plus grande précaution). Le calcul de Denis Poisson. J'ai dû me rabattre sur la fente lumineuse et l'obstruction équivalente pour élaborer cette présentation. En effet, son calcul est plus simple et il est aussi plus facile de vérifier l'ombre d'un fil à l'aide d'un petit pointeur laser. De plus les diagrammes montrent que l'ombre d'un écran circulaire présente des variations significatives selon la distance, ce qui n'est pas le cas d'une fente et de l'obstruction équivalente. Il faut préciser ici, en toute objectivité, que le calcul de Poisson était basé sur l'hypothèse inverse, une sorte d'application du principe de Babinet. La figure de diffraction produite par une obstruction circulaire résulterait de l'addition de milliers d'ondelettes de Huygens provenant du plan comprenant cette obstruction, mais uniquement à l'extérieur d'elle. Un lecteur m'a aussi informé que M. Richard Feynman aurait fait la même démonstration, mais je n'ai pas encore réussi à le vérifier.En définitive, il faut donc admettre que les deux hypothèses sont possibles. Elles se calculent différemment mais elles donnent les mêmes résultats. Et ces résultats se vérifient expérimentalement. Désormais, on peut donc considérer que la lumière pourrait tout aussi bien traverser les objets. Je l'admets, c'est une hypothèse qui semble tout à fait farfelue. Mais voilà : non seulement elle se justifie, mais elle est sans doute exacte.
L'ÉLECTRON ET LA TACHE D'AIRY On a vu à la page précédente que plus l'angle d'ouverture d'un faisceau de rayons lumineux augmente, plus l'ellipsoïde d'Airy raccourcit jusqu'à devenir finalement sphérique. De plus, l'onde qui traverse le plan focal atteint étonnamment le double de la vitesse normale des ondes (c'est à dire c) et sa longueur augmente à cet endroit jusqu'à atteindre une onde entière, ce qui se traduit par une inversion de phase complète. Toutefois il s'agit toujours d'ondes progressives. Mais si les rayons proviennent de chaque côté de l'axe, donc de toutes les directions sur 360°, on obtient évidemment des ondes stationnaires sphériques et concentriques. Tout ceci peut être représenté de la manière suivante : |
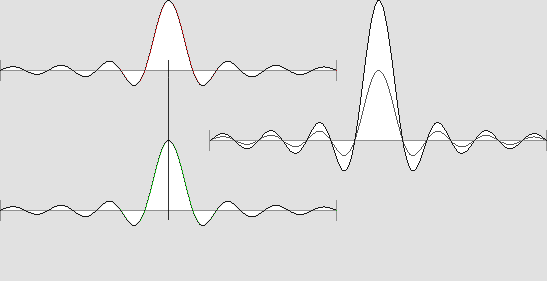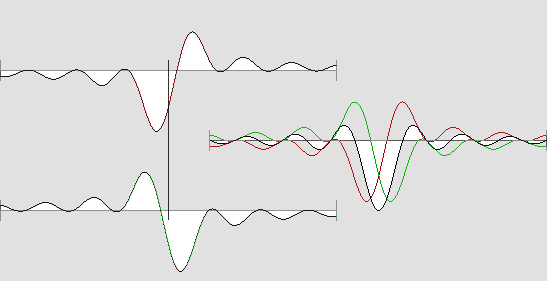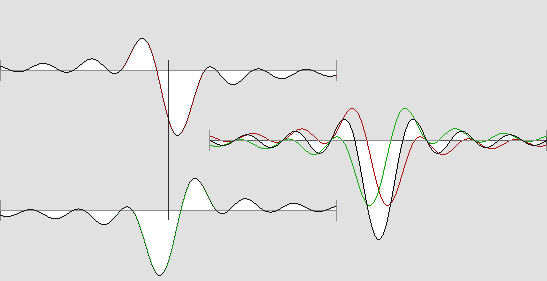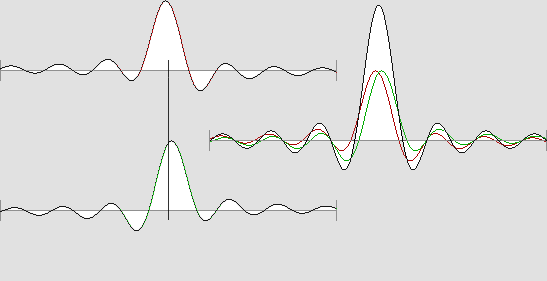
Les variations de l'amplitude.

Cette vue en relief est artificielle. En réalité, le noyau central est sphérique.

La tache d'Airy à pleine ouverture affecte la forme d'ondes stationnaires sphériques et concentriques.
|
On observe que le diamètre du noyau central mesure exactement une longueur d'onde. Les couches successives qui l'entourent comme dans un oignon mesurent chacun une demi-longueur d'onde, de manière à ce qu'une période complète mesure aussi une longueur d'onde. Je tiens à rappeler qu'à ma connaissance, c'est M. Milo Wolff qui a présenté le premier une analyse exacte de ce phénomène. C'est lui qui a remarqué l'inversion de phase qui se produit au centre, et il a compris le premier qu'il s'agissait bel et bien d'un électron. Ce système a ceci de particulier que chaque couche successive contient la même quantité d'énergie. Puisque le volume de chaque couche augmente avec la distance, l'énergie décroît selon la loi bien connue du carré de la distance. L'électron est une sphère d'Airy. Or il se trouve que c'est la structure exacte de l'électron tel qu'il est présenté dans ces pages, du moins lorsqu'il est parfaitement au repos. Tout ceci est absolument remarquable, pour ne pas dire hallucinant.Toutefois, l'électron peut se déplacer par effet Doppler et alors sa structure devient nettement plus complexe. J'ai déjà entrepris à l'aide du médium virtuel de M. Delmotte de mettre en route une nouvelle science : l'optique du mouvement. Il ne fait aucun doute que la structure de la tache d'Airy elle-même se contracte sur l'axe du déplacement comme le prévoyait Lorentz si la source se déplace à grande vitesse. Une tache d'Airy mobile est bien évidemment affectée par l'effet Doppler, ce qui signifie qu'elle est soumise aux transformations de Lorentz. Vous pouvez déjà observer comment une tache d'Airy mobile en deux dimensions se comporte : Bradley_Aberration_Plain.5c.mkv Bradley_Aberration.5c_Scan.mkv On note que les ondes inclinées à cause de l'effet Doppler produisent malgré tout une figure de diffraction et que même la parabole doit se contracter selon les prévisions de Lorentz. Dans la deuxième vidéo, mon Scanner du Temps montre comment un observateur qui se déplace avec ce système devrait voir la scène. Étonnamment, l'effet Doppler s'en trouve annulé de telle sorte que cet observateur a l'impression d'être au repos. Il est clair que tous ceux qui avaient rejeté toute idée d'une contraction devront réviser leur analyse. L'étude des ondes dans un référentiel en mouvement montre que cette contraction prédite par Lorentz est incontournable. Elle doit se produire. En conclusion. Si vous êtes parvenu à ces lignes sans sourciller, c'est non seulement parce que l'optique vous intéresse, mais encore parce que vous n'avez pas peur de sortir des sentiers battus. Notre but est de trouver une explication à la matière, et pour y parvenir il est essentiel de bien connaître les ondes. Désormais, l'étude de la matière relèvera de l'optique. À mon sens, la tache d'Airy en est la preuve la plus éclatante. |
|
Gabriel LaFrenière, Bois-des-Filion en Québec. Sur l'Internet depuis septembre 2002. Dernière mise à jour le 24 octobre 2009. Page d'accueil : La matière est faite d'ondes. Courrier électronique : veuillez consulter cet avis. La théorie de l'Absolu, © Luc Lafrenière, mai 2000. La matière est faite d'ondes, © Gabriel Lafrenière, juin 2002. Optique des miroirs, © Gabriel Lafrenière, juillet 2001. ISBN 2-9806972-2-2 |