LA COURBURE DE CHAMP
|
|
La lentille Oeil d'Aigle.
L'image qui se forme à son foyer est parfaite à tous points de vue.
Qui donc osera prétendre qu'elle a un défaut ?
![]()
![]() Page
d'accueil : La matière est faite d'ondes.
Page
d'accueil : La matière est faite d'ondes.
|
Un rappel. Cette page appartient à une suite qui se nomme "L'optique délinquante". Vous pouvez donc vous attendre à ce que l'optique traditionnelle ou académique y soit critiquée, mais j'espère bien que ce l'est d'une manière constructive. Ludwig von Seidel a "décidé" en 1845 que la courbure de champ était une aberration. Depuis, tous les opticiens se comportent comme des moutons de Panurge. Comme ce fut très souvent le cas en physique, ils n'ont jamais remis en question ce qui semble devenu un dogme inviolable. Comme d'habitude, il existe une raison qui justifie un tel comportement. Dans le cas présent, c'est certainement parce qu'à l'époque, on mettait les meilleures lentilles à l'épreuve en recueillant les images sur des lames de verre planes recouvertes de gélatine imprégnée de sels d'argents. Bien évidemment, on n'avait rien à gagner à recourir à des lames cylindriques ou sphériques dont le rayon de courbure invariable n'aurait pas pu s'adapter aux différentes focales des lentilles à champ sphérique. Ce problème existe toujours aujourd'hui, mais avec la différence que nous fabriquons maintenant des caméras électroniques dont la résolution est ahurissante. De plus, il est possible de coupler les pixels (c'est la signification du sigle CCD). En pratique, en disposant de 10 mégapixels et d'une lentille grand angle, on peut obtenir une image couvrant un angle de champ plus normal tout simplement en la recadrant. De la même manière, une caméra munie d'une lentille à pupille plus grande couvrant un angle de champ normal peut devenir un téléobjectif. Mais pour y arriver il est essentiel que la précision de la lentille atteigne les dimensions de la tache d'Airy. Or la plupart des lentilles à grande pupille actuelles n'y arrivent pas, alors que c'est justement la qualité la plus remarquable des lentilles à champ sphérique. De plus, et c'est encore plus grave, Seidel avait prétendu qu'il existait une configuration pour laquelle une lentille à champ plat ne produisait aucune distorsion. Encore une fois, il y a erreur. J'affirme avec la plus grande énergie que la seule manière de recueillir une image qui soit véritablement exempte de distorsion est de recourir au champ sphérique. La voûte étoilée. Il est bien évident qu'une reproduction montrant comment toutes les étoiles apparaissent dans le ciel devrait être faite à l'intérieur de la surface d'un globe sphérique. Il faudrait faire la même chose dans le cas d'un paysage couvrant tout l'horizon sur 360°, dans le but de lui restituer son aspect original. On peut se demander alors comment il se fait qu'une telle évidence soit rarement envisagée par les opticiens. Au lieu de reconnaître qu'il s'agit d'une approche valable, ils persistent à préférer le champ plat et ils considèrent toujours que la courbure de champ est une aberration. Cette page montre qu'il serait avantageux de munir les caméras électroniques de lentilles à champ sphérique. Dans un premier temps, dans le but de préserver la compatibilité avec les systèmes numériques actuels, on propose ici d'adopter la projection cylindrique. On y trouvera aussi des exemples d'instruments d'optique à champ courbé dont la distorsion est nulle, qui dispersent moins de lumière et qui sont plus précis que les systèmes à champ plat. Ce changement de cap devrait donner un nouveau souffle au cinéma, à la télévision en haute définition et à la photographie. La matière est faite d'ondes. Je suis un passionné d'optique et de photographie depuis la plus jeune enfance. Après deux tentatives en format 127 puis 24 x 36 mm, j'ai finalement construit en 1968 un stéréoscope et un appareil muni de deux caméras 6 x 6 cm synchronisées. Ce système permet de réaliser des diapositives en relief d'un réalisme saisissant. Étrangement, ces diapositives s'accommodent très bien du champ plat, parce que les lentilles du stéréoscope restituent parfaitement la perspective. On observe en effet l'image de face et selon le même angle de champ que la caméra. Il n'empêche que ce système fonctionnerait mieux en mode sphérique. En 1993, j'ai décidé de polir moi-même les miroirs de mes télescopes. Je me suis procuré le matériel à la Maison de l'Astronomie de Montréal, qui demeurera toujours à mes yeux l'équivalent de la caverne d'Ali Baba. Il m'a fallu aussi apprendre la programmation sur ordinateur pour peaufiner les calculs. J'utilisais au début un ancien modèle très lent (1 MHz ?) sans disque dur (XT 640 k) fonctionnant sous l'antique MS- DOS. Ce fut le début d'une aventure merveilleuse qui m'a permis de rédiger un ouvrage intitulé Optique des miroirs. Il décrit plus d'une centaine d'instruments à miroirs que j'ai vérifiés par ordinateur pour la plupart, un grand nombre comportant des lentilles ou des correcteurs en verre optique. Plus d'une trentaine ne sont décrits nulle part à ma connaissance, et il pourrait donc s'agir d'inventions originales. On y montre en particulier que tous les appareils munis de lentilles pourraient tout aussi bien utiliser des miroirs, d'où le concept de "lentilles à miroirs". Parce que l'interféromètre de Michelson est aussi un appareil d'optique à miroirs, cette aventure a débouché sur une découverte tout à fait stupéfiante : la matière est faite d'ondes exclusivement. En effet, puisqu'elle se contracte comme Lorentz l'a proposé, elle ne peut être faite que d'ondes stationnaires sphériques, dont le prototype est montré à la page d'accueil. C'est pourquoi les opticiens ont désormais une longueur d'avance en physique nucléaire puisque l'optique fait une large place à l'étude des ondes. La courbure de champ. L'ouvrage Optique des Miroirs (tout aussi délinquant) comporte une annexe qui bouscule nettement les principes généralement admis en optique. En particulier j'y démontre que le champ plat si cher à Seidel et à Petzval est une aberration. Tôt ou tard on devra privilégier plutôt le champ courbé. Cet aspect du cinéma et de la photographie me tient particulièrement à cœur, à un point tel que j'ai pris la peine de faire cette page. Vers 1845 Ludwig von Seidel a mis au point une série d'équations permettant de corriger les aberrations suivantes, et qui portent le nom de sommes de Seidel :
On constate que Seidel considère que la courbure de champ est une aberration. Son contemporain Petzval, qui pensait de même, est l'auteur d'une loi voulant que le rayon de courbure du miroir secondaire d'un télescope de Cassegrain doit être le même que celui du primaire pour obtenir ce sacro-saint champ plat. Plus exactement, celui du secondaire étant négatif, la somme des rayons de courbure doit être égale à 1, et c'est valable quel que soit le nombre de miroirs. Et depuis, tous se prosternent devant cette erreur. Le champ plat est une aberration. Car il s'agit bien d'une erreur. Parce que les caméras étaient depuis le début assujetties aux plaques photographiques en verre plat, il était difficile de se rendre compte que la difficulté provenait précisément de ces plaques. L'avènement du film en matière plastique a failli renverser la vapeur. La première moitié du 20e siècle a vu apparaître des caméras populaires munies de lentilles double ménisque, et dans lesquelles le film était courbé, donc cylindrique. Ces caméras produisaient des images qui apparaissent absolument sans distorsion, peu importe l'angle de champ (même sur 360°), pourvu qu'elles soient affichées sur un écran cylindrique dont le rayon de courbure est proportionnel au grandissement. Malheureusement, l'arrivée des caméras compactes 24 x 36 mm de type Leica a compromis ce retour à la raison. Munies de lentilles à champ plat de plus en plus lumineuses (ƒ/2 et même moins), elles permettaient de photographier des scènes peu éclairées à 1 / 125e de seconde, et les photographes en ont oublié leurs notions d'optique les plus élémentaires. Ils auraient dû comprendre que la difficulté provenait encore une fois du film. Il est évident que si la sensibilité et la précision des émulsions avaient été cent fois plus grandes, ils en auraient profité pour améliorer plutôt la qualité de leurs photographies. Il faut savoir qu'une lentille ƒ/ 1,4 de 50 mm produirait idéalement 216 millions de taches d'Airy de 0,002 mm et donc au moins autant de pixels bien séparés sur une surface faisant 24 x 36 mm. Or la précision des films et des lentilles atteignait à peine 0,025 mm. Les manufacturiers (sauf Zeiss) ne se gênaient pas pour évaluer la profondeur de champ de leurs lentilles selon une norme de 0,035 mm et parfois plus alors qu'en réalité elle est presque inexistante s'il faut respecter la tache d'Airy. Faites le calcul : (24/0,035)*(36/0,35) = 705 306 pixels, c'est à dire moins d'un mégapixel, sans oublier le fait que la surface du négatif était rarement utilisée en entier. En conséquence, toutes les photographies réalisées au 20e siècle à l'aide des caméras 24 x 36 mm sont lamentablement floues et irrécupérables. C'est seulement depuis l'arrivée des caméras numériques qu'on s'en rend compte finalement. Beaucoup d'artistes prétendront que c'était bien suffisant et même intentionnel, mais faut-il vraiment les croire ? Seuls les photographes les plus consciencieux (et les plus fortunés) utilisaient des négatifs plus grands, par exemple 6 x 6 cm. Les professionnels privilégiaient même les caméras 4" x 5", la plus célèbre étant la Graflex Speed Graphic, soit l'équivalent de 10 x 13 cm environ. Ils en obtenaient des photographies magnifiques, d'autant plus qu'ils étaient conscients que les lentilles dont l'ouverture relative est plus élevée préservent beaucoup mieux la tache d'Airy. Bref, on agissait ainsi parce qu'on manquait de lumière. Tout est bien différent autrement car on peut réduire la taille de la pupille d'entrée jusqu'à ce que la profondeur de champ atteigne le maximum possible compte tenu de la résolution en mégapixels. Cela permet en particulier de profiter d'une hyperfocale étendue et même fixe : le "sténopé à lentille" en particulier n'a pas besoin de bague de mise au point. Les caméras numériques. Les caméras numériques ont révolutionné le cinéma et la photographie :
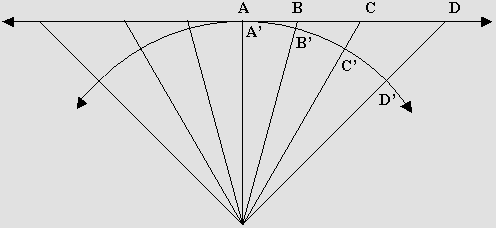
La projection cylindrique. Il existe de nombreux types de projections, mais on comparera ici la projection cylindrique (qui demeure azimutale sur le plan vertical) et la projection plane totalement azimutale. C'est cette dernière que Seidel a envisagée, tout comme les peintres de la Renaissance d'ailleurs. Le sténopé montré plus loin servira d'exemple. Si sa surface photosensible était sphérique et centrée sur la pupille, l'image obtenue serait tout à fait exempte de distorsion. Toutefois, cela conduit à des problèmes difficiles à régler. Par exemple, il serait plus difficile de numériser une image sphérique parce que les pixels ne peuvent pas y être répartis de manière uniforme. Mais si la surface photosensible est cylindrique, la compatibilité avec les images actuelles peut être préservée. Au besoin la projection cylindrique originale peut facilement être convertie par l'ordinateur en projection de Mercator. Il s'agit de la méthode inventée en 1569 par le cartographe du même nom, et qui permettrait en photographie de maintenir (partiellement) la proportion des objets s'il fallait sélectionner une partie de l'image situé dans un coin, dans le but de l'agrandir. En effet, sur une projection de Mercator représentant la Terre, la surface relative des continents double au 45e degré de latitude (à Montréal ou à Bordeaux) et elle est donc considérable près des pôles. Ainsi le Groenland y apparaît gigantesque malgré sa taille relativement modeste. Par contre, ses proportions sont moins déformées. Mais il n'y a pas lieu de paniquer, car c'est encore pire avec le champ plat. De plus il est très rare qu'un photographe utilise une lentille très grand angle capable de couvrir 155° à la verticale, le centre du Groenland étant à 25° environ du pôle nord. Le format 16 : 9 des écrans HDTV réduit considérablement ce risque. De plus, même si le visage d'une personne vue sous cet angle y semblerait agrandi, il n'en serait pas outrageusement défiguré, ce qui est inévitable avec le champ plat azimutal. Pas de distorsion. Une photographie prise en format cylindrique et qu'on reproduit sur un écran cylindrique ne présente absolument aucune distorsion si elle est observée au centre de courbure et au niveau central de cet écran. L'écran peut même entourer le spectateur, les montages sur 360° étant facilement possibles. Un visage y apparaît absolument intact n'importe où, parce que l'angle de visée et la distance varient de la même manière que lors de la prise de vue.Pour être honnête, la photographie elle-même présente une distorsion aux endroits éloignés de l'axe central, donc surtout dans le haut et le bas de l'écran, mais l'angle de vue annule cette distorsion si les conditions sont respectées. La projection plane azimutale. On obtient une projection azimutale d'un continent figurant sur le globe terrestre en y déposant une surface plane et en y reportant ses contours, vus du centre du globe. Cette méthode produit beaucoup de distorsion en périphérie. Elle ne peut représenter qu'un seul hémisphère, mais il est possible de reproduire le globe entier sur une projection azimutale dite équidistante, les parallèles y apparaissant équidistants. On obtient alors une image de type fish eye, mais la distorsion y est plus sévère encore. Dans tous les cas, seule la partie située près du centre sera exempte de distorsion. Toutefois la surface d'un globe terrestre est sphérique alors que les lentilles à champ plat sont plutôt conçues pour reproduire (prétendument sans distorsion) une surface également plane. La façade d'un gratte-ciel, par exemple, semble intacte vue de face parce que les lignes parallèles de l'édifice sont préservées. Mais ce n'est qu'un leurre. Dans les coins en particulier, l'image d'un objet s'en trouve fâcheusement étirée si on l'observe perpendiculairement à la surface. La projection cylindrique. On obtient plutôt une projection cylindrique en procédant de la même manière, mais en remplaçant la surface plane par une surface cylindrique entourant le globe. Alors tous les points du globe en contact avec le cylindre deviennent libres de distorsion. Le gain est donc très net sur toute la longueur d'un axe qui traverse l'image, de préférence l'axe horizontal. La projection cylindrique offre aussi l'avantage de pouvoir choisir l'axe, qui n'est pas nécessairement celui de l'équateur. Il est très possible de faire passer cet axe par les deux pôles de la Terre et d'obtenir une carte relativement fidèle incluant ces deux pôles, et par exemple l'Amérique du nord et l'Amérique du sud, sans oublier l'axe passant par la Sibérie et la Chine, de l'autre côté de la Terre. Cet axe peut donc être vertical, mais il peut aussi être déporté. Il peut même être incliné, sachant que la projection de Mercator oblique, qu'on découvre à l'heure actuelle, permet d'allonger encore cet axe à cause de la diagonale. Elle permet par exemple de le faire passer par deux visages très éloignés l'un de l'autre dans le but de sauvegarder leurs proportions ou de les agrandir individuellement. Ce sont des choix qui ne sont pas possibles avec une lentille à champ plat. Le défaut de la projection azimutale est donc toujours présent dans la projection cylindrique, mais uniquement sur le plan vertical. Il est toutefois réduit considérablement puisqu'il n'existe plus tout le long de l'axe horizontal d'une part, mais aussi parce que l'image couvre généralement un angle beaucoup plus faible verticalement. La projection de Mercator. De plus, la distorsion azimutale est beaucoup plus facile à corriger si nécessaire puisqu'elle n'a lieu que sur un axe vertical. Il est même possible de recourir à différentes corrections verticales dès la prise de vue puisqu'il existe toute une gamme de projections dont la plus célèbre est celle de Mercator, qui n'est pas azimutale. D'ailleurs, puisque la luminosité faiblit toujours sous un certain angle à cause de l'inclinaison de la pupille, on a intérêt à faire les capteurs CCD un peu plus hauts, donc rectangulaires, pour compenser. Un peu de trigonométrie. Le diagramme montré ci-dessous fait ressortir la différence entre le champ courbé et le champ plat. Il faut préciser qu'il représente l'intérieur de la caméra. On constate d'abord qu'une image plane peut difficilement couvrir un angle de champ bilatéral supérieur à 90°. Le faisceau lumineux D atteint alors le « plan » focal sous un angle de 45°, ce qui implique une distorsion valant le cosinus de cet angle, soit 0,7 : 1. Or plus loin cette distorsion augmente ensuite de manière catastrophique. |
|
Au contraire la distorsion est nulle au point D' parce que l'angle d'arrivée du faisceau comparativement à la surface photosensible demeure constant à 90°. Le champ courbé permet aussi de conserver une luminosité plus uniforme, d'abord parce qu'une surface inclinée reçoit moins de lumière, mais aussi parce que le point D est plus éloigné. Le champ plat est préférable lorsqu'il s'agit de reproduire l'image d'une surface plane, comme celle d'un document. Dans ce cas il faut reconnaître que l'angle de visée provoque une distorsion qui sera compensée. Par exemple, l'image plane d'un ballon parfaitement sphérique apparaît sous la forme d'une ellipse aplatie si elle est observée sous un certain angle. Alors la distorsion montrée ci-dessus compense, et le cercle se reforme. Toutefois l'image d'un véritable ballon sera étirée. On obtient une compensation semblable sur une projection de Mercator, soit à l'infini, soit sur une surface sphérique et dans un espace en trois dimensions. Toutefois, sachant qu'il n'est pas possible de placer le même nombre de ballons sphériques sur le 45e parallèle que sur l'équateur, ces ballons qui apparaîtront circulaires sur la photographie y seront malencontreusement agrandis selon la réciproque du cosinus de 45°, soit 1,414. Leur aire sera donc doublée exactement, comme on le montre ci-dessous, à gauche. Ce diagramme ne présente qu'une partie du problème, car on pourrait aussi représenter comment la lentille à champ plat reproduit des ballons sphériques placés sur une surface plane, ou comment une caméra à champ cylindrique reproduit une surface plane, etc. Ici on a choisi de comparer le champ cylindrique et le champ plat en supposant que des ballons soient disposés sur une surface sphérique, la pupille de la caméra se situant au centre de courbure. |
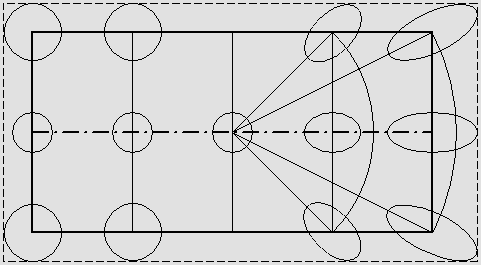
À gauche, la projection cylindrique permet de préserver la forme circulaire, mais les proportions ne sont pas conservées.
Il peut exister différentes corrections régissant la distorsion verticale, qui n'est pas nécessairement azimutale.
À droite, la projection azimutale à champ plat.
|
La partie de gauche représente donc comment un champ cylindrique peut reproduire des ballons sphériques placés sur une surface sphérique. Sans correction verticale azimutale, ces ballons apparaîtraient tous circulaires et identiques sur un écran cylindrique, mais il s'agit ici de montrer que l'ordinateur peut corriger les ellipses sur son écran plat de manière à ce qu'elles redeviennent circulaires. Cette correction fonctionne mieux si les ballons sont petits. Autrement ils apparaîtront ovoïdes. À droite, l'image des ballons est forcément elliptique ailleurs que près du point de fuite central. Parce que la distorsion prend effet à partir de ce point de fuite et non à partir de l'axe horizontal, les ballons apparaissent beaucoup plus étirés s'ils sont placés dans les coins. Ce problème d'étirement en diagonale n'existe pas sur une projection cylindrique. Ici aussi l'ordinateur peut les comprimer de manière à ce qu'ils apparaissent de nouveau circulaires, mais ce serait plus difficile à réaliser et il en résulterait par ailleurs une forte distorsion (appelée "baril" en anglais : barrel distorsion, soit le contraire de pincushion ou "coussin à épingles"). Comme on l'a vu plus haut dans le cas d'un stéréoscope, il est possible de faire en sorte qu'une telle situation ne provoque pas de distorsion perceptible. Il s'agit le plus souvent de respecter le point de fuite bien connu des dessinateurs. Mais en pratique elle se réalise rarement et elle présente des inconvénients qui sont beaucoup plus sévères dans le cas du champ plat. La perspective et le point de fuite. C'est donc cette façon de faire dite "sans distorsion" qui a été retenue par Seidel et Petzval. Elle a pour effet de rétablir horizontalement et verticalement les lignes parallèles d'un édifice, par exemple, s'il est vu de face. Mais c'est expressément à la condition que l'observateur soit placé exactement face au point de fuite de l'image. Mais ce n'est pas tout : il faut aussi qu'il soit à la distance qui respecte cet angle de champ. Or la plupart des gens n'auront pas le réflexe d'en tenir compte. Tous les peintres de la Renaissance ont utilisé cette méthode, dont Raphaël et Léonard de Vinci. Mais aucun n'a poussé l'audace jusqu'à provoquer délibérément la distorsion requise jusque dans le dessin des personnages. Le problème, c'est que si ces personnages sont placés dans les coins d'un tableau, il n'est plus possible de les regarder en face sans constater cette distorsion. Ils l'ont donc corrigée, créant intentionnellement une anomalie qui jette un peu d'ombre sur la perfection de leurs oeuvres... Très clairement, la perfection absolue aurait été de recourir à des toiles sphériques. Pour la même raison, c'est le champ sphérique qui est parfait et qui ne présente aucune distorsion. Les images à champ plat dites sans distorsion souffrent de . . . distorsion. Comme on l'a vu ci-dessus, la distorsion sous un angle de 45° atteint 0,7 : 1. Une telle distorsion ne peut plus passer inaperçue. L'image d'un personnage réel qu'un photographe inexpérimenté aurait située dans le coin supérieur droit d'une photographie réputée sans distorsion serait déformée comme on le montre ci-dessous, à droite. Ce personnage en sera vraisemblablement outré. Quiconque tenterait de réparer les dégâts devrait déployer des moyens hors du commun à l'aide de Photoshop. C'est d'ailleurs ce qu'il a fallu faire ici en sens inverse, et avec l'immense avantage de connaître à l'avance à la fois l'angle radial et l'angle de champ. |
|
|
|
|
Ce problème peut être évité. L'avantage indiscutable de la projection cylindrique, c'est que la distorsion est nulle tout le long d'un axe horizontal qui détermine l'équateur d'un champ courbé. Cette distorsion n'a lieu qu'en fonction de l'angle rapporté à cet axe et non pas au point de fuite. Elle ne se fait jamais obliquement. Elle est donc beaucoup moins dommageable dans tous les cas. La caméra électronique ou l'ordinateur peuvent rétablir les cercles d'un simple clic (choix entre la projection cylindrique originale et celle de Mercator, ou toute autre variante au choix). Aucun détail de l'image ne sera donc déformé comme on le voit ci-dessus. La distorsion verticale est d'ailleurs très faible lorsque la largeur de l'écran est à peu près deux fois plus grande que sa hauteur. C'est le cas au cinéma (Panavision, Cinémascope) ou sur un téléviseur à haute définition de format 16 : 9. La compression de l'image sur les côtés d'un écran plat à cause de l'angle de visée n'est pas significative psychologiquement et ce problème sera résolu dès qu'on réalisera que l'écran devrait être cylindrique. Il est possible qu'on fasse les écrans sphériques dans un avenir éloigné. Ce serait certainement avantageux. |
![]()
LES APPAREILS À CHAMP COURBÉ
|
On montre ci-dessous quelques exemples de caméras à lentille ou à miroir dont le champ est courbé. Les sténopés à lentille. Le sténopé est une caméra sans lentille, celle-ci étant remplacée par une simple perforation dont le diamètre est très faible. Il s'agit d'une invention chinoise, qui daterait d'environ 500 ans avant notre ère. Considérant les performances des nouvelles surfaces photosensibles électroniques, on peut imaginer le modèle suivant, qui serait capable de produire des photographies étonnantes malgré sa lentille rudimentaire : |
|
|
Le sténopé, l'antique camera obscura.
La surface photosensible doit être cylindrique.
La lentille double ménisque, facultative, améliore considérablement la précision.
|
On trouvera une description plus complète de cet appareil à la page sur le sténopé. La précision et le contraste de la photographie sont bien meilleures si la perforation est munie d'une lentille très faible, préférablement de type concentrique (on a opté ici pour une lentille double ménisque, qui est achromatique). On profite ainsi à la fois des avantages de la lentille, dont la précision est remarquable à faible ouverture, sans sacrifier les avantages non négligeables du sténopé. Même si le sténopé est en principe une caméra sans lentille, il demeure possible d'envisager un "sténopé à lentille" en conservant la très petite pupille conduisant à une ouverture relative de ƒ/ 50 ou même plus, dépendant de l'angle de champ vertical. La partie ombrée montre les zones où la mise au point est bonne. On peut constater que même si la surface photosensible apparaît droite en élévation, elle demeure à l'intérieur de cette zone. Sur un plan horizontal cette surface est courbée de manière à coïncider avec les pointillés, qui correspondent à l'hyperfocale. Ainsi la tache d'Airy est préservée quel que soit l'angle de champ, qui peut atteindre facilement et même dépasser 90°. De nombreuses caméras du début du 20e siècle ont été construites de cette manière mais leurs performances étaient décevantes à cause de la piètre sensibilité du film utilisé à l'époque. Le point important, c'est que toutes les lentilles et miroirs convergents qui produisent un champ courbé permettent d'obtenir à la fois une image comportant peu ou pas de distorsion, avec en prime une tache d'Airy bien plus précise. |
![]()
|
La caméra Mercator. Peu de gens savent que le cristallin de l'œil agit très peu en tant que lentille. Il agit surtout en modifiant le rayon de courbure de la cornée, qui est convexe. On peut mettre à profit ce principe en construisant une caméra tout à fait remarquable faite d'un seul bloc de plastique léger. Cette lentille est tellement simple que quelqu'un, quelque part, en a sûrement fait une description élaborée. Pourtant je n'ai jamais réussi à en trouver la moindre trace et j'ai donc dû la « réinventer ». À tout hasard je lui ai donné ce nom de Oeil d'Aigle, au cas où elle ne figurerait nulle part. Une chance sur mille. Il est inutile d'indiquer les distances puisqu'elles correspondent aux rayons de courbure. Cette lentille est sans doute connue depuis longtemps mais elle n'est jamais montrée ni utilisée, sans aucun doute parce qu'elle produit une image sphérique, ce qui selon Seidel est une aberration. Pourtant il ne faut pas l'examiner longtemps pour réaliser que Seidel s'est mis le doigt dans l'œil. Les systèmes parfaitement sphériques et concentriques (ou monocentriques) sont toujours exempts de coma et d'astigmatisme, peu importe l'angle de champ. L'aberration de sphéricité peut facilement être corrigée en ajustant le rayon de courbure terminal (ici R 6). L'aberration chromatique demeure à l'intérieur de la tache d'Airy pour toutes les couleurs y compris le violet, même avec une pupille de 10 mm ƒ/ 2. |
|
|
La caméra Mercator.
LES SYSTÈMES PARFAITEMENT SPHÉRIQUES ET CONCENTRIQUES
|
La lentille Oeil d'Aigle. Peu de gens savent que le cristallin de l'œil agit très peu en tant que lentille. Il agit surtout en modifiant le rayon de courbure de la cornée, qui est convexe. On peut mettre à profit ce principe en construisant une caméra tout à fait remarquable faite d'un seul bloc de plastique léger. Cette lentille est tellement simple que quelqu'un, quelque part, en a sûrement fait une description élaborée. Pourtant je n'ai jamais réussi à en trouver la moindre trace et j'ai donc dû la « réinventer ». À tout hasard je lui ai donné ce nom de Oeil d'Aigle, au cas où elle ne figurerait nulle part. Une chance sur mille. |
|
|
La lentille « Oeil d'Aigle ».
Un jour, toutes les lentilles seront construites de cette façon.
Aucune lentille au monde ne produit une image aussi précise sur un aussi grand angle de champ.
On peut construire une version à deux ménisques identiques, donc parfaitement symétrique.
Elle pourrait avantageusement être plutôt remplie d'huile d'indice de réfraction convenable.
Cela permettrait d'y placer un diaphragme, mais j'ai aussi songé à un iris à cristaux liquides !
| Ménisque | R 1 = 26,19 mm | Verre 803304 LaSF 32 | R 2 = 10 mm |
| Élément plano-convexe | R 3 = 10 mm | Verre 713538 Lak 8 | R 4 = plano |
| Pupille maximum | D = 6,18 mm | Pupille virtuelle : 10 mm | |
| Élément plano-convexe | R 5 = plano | Verre 713538 Lak 8 | R 6 = – 27,227 mm |
| Champ sphérique | R 7 = – 40 mm | Focale : 40 mm | Ouverture : ƒ/ 4 |
|
Il est inutile d'indiquer les distances puisqu'elles correspondent aux rayons de courbure. Cette lentille est sans doute connue depuis longtemps mais elle n'est jamais montrée ni utilisée, sans aucun doute parce qu'elle produit une image sphérique, ce qui selon Seidel est une aberration. Pourtant il ne faut pas l'examiner longtemps pour réaliser que Seidel s'est mis le doigt dans l'œil. Les systèmes parfaitement sphériques et concentriques (ou monocentriques) sont toujours exempts de coma et d'astigmatisme, peu importe l'angle de champ. L'aberration de sphéricité peut facilement être corrigée en ajustant le rayon de courbure terminal (ici R 6). L'aberration chromatique demeure à l'intérieur de la tache d'Airy pour toutes les couleurs y compris le violet, même avec une pupille de 10 mm ƒ/ 2. Je tiens à préciser qu'une pupille de 10 mm permet de recueillir des tas de mégapixels, de telle sorte que cette lentille à très grand angle est aussi un téléobjectif. Oubliez les lentilles interchangeables ! La lentille Sutton Waterlens. |

Il existe une lentille semblable appelée Sutton Waterlens, dont le centre est rempli d'eau.
Cela permet d'y placer un diaphragme à iris.
Ici, le champ est cylindrique, ce qui est un compromis acceptable qui exige cependant des dimensions beaucoup plus imposantes.
Idéalement, la surface photosensible (CCD) devrait être sphérique car alors la caméra serait minuscule : deux ou trois centimètres !
|
J'ai ajouté le présent paragraphe en janvier 2007 pour remercier celui qui se fait appeler « Seba ». C'est grâce à lui que je peux citer cette lentille ici. En bon photographe, ce membre du forum Chasseurs d'Images est « objectif ». Lisez ses commentaires : ça vaut le coup. Les anneaux de la tache d'Airy sont plus lumineux à grande ouverture. Toutefois rien n'est parfait et les choses se gâtent à ƒ/ 1 avec une lentille de type Oeil d'Aigle, du moins avec une pupille de 10 mm. La tache d'Airy mesurerait alors aussi peu que 0,0013 mm. D'ailleurs on montre à la page sur la tache d'Airy que la luminosité relative des anneaux augmente d'une manière catastrophique à très grande ouverture, ce qui conduit à une perte de contraste. De plus la mise au point devient très difficile à réaliser. Bien que beaucoup de systèmes concentriques soient capables d'atteindre en principe des valeurs inférieures à ƒ/ 1, tout indique qu'il faudra les éviter à tout jamais. Cela signifie qu'on ne réduira sans doute jamais non plus les dimensions des capteurs CCD à moins d'un micromètre, sauf dans certains cas particuliers.Plus raisonnablement, la lentille Oeil d'Aigle 40 mm ƒ/ 4 possède un pupille virtuelle de 10 mm mais le diamètre réel de l'iris n'est que de 6,18 mm. Elle ne mesure que 53,4 mm sur l'axe central. Elle ferait une tache d'Airy de 0,0053 mm et un champ de 63 x 63 mm. Une pupille de 10 mm produit donc idéalement 140 mégapixels sur 90°, ce qui est vraiment remarquable. On pourrait évidemment coupler les pixels pour augmenter la luminosité ou s'en servir comme téléobjectif en n'utilisant que les pixels centraux, ce qui élimine la nécessité de changer de lentille. Il faut rappeler qu'une pupille de 10 mm permet théoriquement de distinguer à un kilomètre deux points lumineux distants de 7 cm seulement. L'ordinateur montre qu'il est possible de construire une lentille à deux ménisques identiques, la lentille devenant alors parfaitement symétrique et réversible. Cette configuration permettra de construire des caméras à lentille rotative, dans le but de faire tourner sa pupille. On sait que toute pupille d'entrée a pour effet de réduire la luminosité selon le cosinus de son angle d'inclinaison. Une pupille rotative peut éliminer ce problème à la condition de synchroniser les pixels, de manière à photographier une scène sur un très grand angle de champ, et même sur 360°. Cela produit une caméra dite Périphote, mais bien plus précise que celle de Louis Lumière. Je n'ai pas encore mis la main sur les spécifications de la version Sutton Waterlens, mais il est évident qu'elle devrait posséder également deux ménisques, symétriques ou non. Au lieu d'eau, l'intérieur devrait idéalement être rempli d'une huile dont l'indice de réflexion et de dispersion permet de la rendre achromatique, compte tenu des ménisques. La présence de l'huile au centre de courbure permet aussi d'y placer un diaphragme à iris. Je rappelle enfin que mon ouvrage Optique des miroirs montre un correcteur semblable utilisable sur un télescope de Schmidt, et dont l'intérieur est plutôt rempli d'un gaz lourd comprimé dans le but d'annuler son effet divergent. Il s'agit en fait d'un double Bouwers, mais il est achromatique et c'est à ma connaissance le seul correcteur qui produise des images aussi précises dans les coins d'une photographie qu'au centre. Bien évidemment, le Schmidt (voir plus loin un modèle replié) possédant par définition une pupille au centre de courbure du miroir, son champ est sphérique et il peut donc produire des photographies sans distorsion de la voûte étoilée. Il en va de même du Schmidt-Cassegrain concentrique, qui est malheureusement beaucoup plus long que le modèle compact classique. Cela suppose que les CCD doivent également être sphériques, et il sera intéressant de surveiller si on disposera les photosites sur des méridiens et des parallèles éventuellement. Les méridiens et les parallèles. Il faudra donc tôt ou tard utiliser une surface photosensible sphérique. Il s'agira de disposer les pixels photosensibles sur des méridiens et des parallèles, comme si l'image se formait sur l'équateur d'un globe terrestre, mais vu de l'intérieur puisque le champ est concave. Ce n'est pas pour demain, mais on pourra alors obtenir au choix une projection de Mercator ou une projection cylindrique orthogonale. De plus la mise au point sera meilleure dans les parties supérieures et inférieures de l'image. L'immense avantage de cette lentille, c'est qu'elle permettra dans un siècle ou deux de construire des caméras vraiment minuscules. En effet, une caméra ƒ/ 1 à pupille de 2 mm mesurera moins de 5 mm. Une telle caméra sera quand même remarquablement précise. Le problème se résume à fabriquer une surface photosensible électronique concave équipée de pixels de 0,001 mm exceptionnellement efficaces, et qui soient disposés sur des méridiens et des parallèles. Ce sera la caméra ultime. En fait il ne sera jamais possible de faire mieux, du moins en termes de dimensions. La championne . . . du champ plat. Le déplacement de la lentille d'une caméra selon la formule de Descartes : L2 = L1 * F / (L1 - F) permet d'effectuer la mise au point sur un objet rapproché. La distance de l'image qui se forme au foyer de la lentille augmente, alors que celle de l'objet diminue. Ainsi, le fait de déplacer une lentille à champ courbé modifie le rayon de courbure du champ côté image, et alors on pourrait craindre que le rayon de courbure constant de la surface photosensible ne convienne plus. Toutefois il se produit une compensation qui fait en sorte que le champ côté objet est toujours plat s'il est rapproché. C'est ce qu'on pourrait appeler le « paradoxe de Descartes ». En plus clair, la lentille Oeil d'Aigle sera parfaitement en mesure d'effectuer la mise au point sur des objets rapprochés, mais ils devront se trouver sur une surface plane. En fait le champ peut être indifféremment plat côté image et sphérique côté objet, ou l'inverse. On aura donc le choix, à la condition que le rayon de courbure de la surface courbée soit toujours égal à la focale. Macrophotographie et microphotographie. Inversement, la même lentille Oeil d'Aigle peut agrandir les images, ce qu'elle fait à merveille sur une large plage. Ce sera donc aussi une excellente lentille pour macrophotographie, dont la particularité sera de pouvoir produire (selon le diamètre de sa pupille) des dizaines de mégapixels sur un très grand angle et donc sur une photographie immense, à ne plus que savoir en faire. Dans le cas des images à peu près grandeur nature (donc avec L1 = L2 = 2 F) , le rayon de courbure de la surface photosensible devrait valoir deux fois la focale de la lentille pour que la distorsion demeure nulle. Ceux qui voudront obtenir à tout prix des images grandeur nature grand angle sans distorsion trouveront sans doute plus simple de remplacer la lentille de leur caméra par une autre de focale deux fois plus courte, ce qui reviendra au même. Ce sera même une excellente lentille de microscope. Mais à cause du fort grandissement, il faudra utiliser idéalement (mais pas nécessairement) une surface photosensible plane. Il faudra donc que les échantillons soient placés entre des lamelles sphériques dont le rayon de courbure soit égal à la focale de la lentille. Cet inconvénient ne surviendrait que s'il fallait obtenir un très grand angle de champ sous une très faible profondeur de champ, ce que d'ailleurs seule cette lentille peut faire. Autrement la surface photosensible peut être courbée et ces lamelles sphériques ne sont pas requises. Une difficulté : oui. Un obstacle : non. Ainsi le champ courbé représente une difficulté, mais ce n'est pas vraiment un obstacle depuis que les surfaces photosensibles électroniques existent. Autrefois il était impensable d'avoir à insérer un film sphérique à l'intérieur d'une caméra (les astronomes le faisaient avec le Schmidt). Il faudra bien qu'on réalise un jour que ce problème n'existe plus.D'ici à ce qu'on parvienne à disposer les pixels photosensibles sur des méridiens et des parallèles, il faudra privilégier le champ cylindrique et les focales relativement longues, de l'ordre de 100 mm. Une ouverture relative élevée de ƒ / 50 et même plus s'avère nécessaire pour éliminer les problèmes de mise au point dans les parties inférieures et supérieures d'une image cylindrique. D'un autre côté, considérant les dimensions de la tache d'Airy, il faut cibler une pupille d'environ 2 mm dans les lentilles grand angle. Une pupille de 2 mm. Si la tendance se maintient entre 5 et 10 mégapixels, ce qui est très acceptable et même parfois superflu, ce diamètre de 2 mm correspondra à une constante, à 0,5 mm près. C'est à cause de la longueur d'onde de la lumière qu'il en est ainsi. On présume ici qu'il vaut mieux dimensionner les pixels selon la tache d'Airy et non selon la limite de Dawes, mais c'est un choix discutable. Une telle pupille fixe élimine la nécessité d'avoir à ajuster un diaphragme à iris. Elle permet d'obtenir un nombre suffisant de pixels sur une grande profondeur de champ, avec la possibilité de laisser la mise au point en permanence sur l'hyperfocale. Ceci ne s'applique évidemment qu'aux caméras grand angle couvrant environ 90°. Les caméras numériques actuelles sont compactes et elles produisent des images magnifiques. Mais on peut faire mieux encore en augmentant leur profondeur de champ tout en éliminant la nécessité de faire la mise au point et de régler le diaphragme. Il faut utiliser des systèmes optiques sphériques et concentriques. Ils sont plus simples et plus précis, ils dispersent moins de lumière et ils occasionnent moins de distorsion s'ils couvrent un grand angle de champ. L'apodisation. Cette pupille de 2 mm pourrait être portée à 4 mm à la condition de l'apodiser. Ce terme signifie qu'elle devrait être munie d'un filtre qui élimine progressivement la lumière en périphérie, idéalement selon la courbe bien connue en forme de cloche, dite de distribution normale. Ce filtre produit une tache d'Airy sans anneaux, et tout indique que la qualité des images en serait sensiblement améliorée. Mais ça reste à démontrer. Vous trouverez plus de détails sur l'apodisation à la page sur le sténopé. Quatre couleurs. Des test très poussés ont montré qu'il serait avantageux d'utiliser quatre couleurs primaires et non trois, aussi bien dans le cas des écrans qu'en imprimerie. La norme « L*a*b* » de la CIE s'avère la meilleure, le vert lime actuel trop lumineux étant réparti plus équitablement dans le jaune et le vert émeraude. Étonnamment, ceci permet de tripler la précision ou les dimensions des images numériques. On trouvera plus de détails, y compris la disposition des CCD, à la page sur la norme à quatre couleurs. L'idée consiste à alterner les axes a et b sur les lignes paires et impaires, et à n'utiliser qu'une seule couleur par pixel une fois sur deux, la couleur complémentaire étant donnée à partir de la luminance des quatre pixels voisins, ceux-ci ne comportant aucune indication de couleur. Ce système devra faire appel à des algorithmes de reconstitution sophistiqués, mais ce sera à la portée des ordinateurs et des téléviseurs de demain. Ces tests ont montré qu'il valait mieux accorder la priorité à la luminance, la couleur pouvant être reproduite avec précision (et même avec un gain à cause de la couleur additionnelle) à la condition qu'elle s'étale sur une surface suffisante. On obtient finalement des images plus précises, et dont les couleurs seraient compatibles avec celles des encres d'imprimerie. Des systèmes sans distorsion, plus précis, plus simples, et qui dispersent moins de lumière. Seuls les systèmes optiques à lentilles ou à miroirs dont les éléments sont sphériques et concentriques permettent d'obtenir des images parfaitement exemptes de coma et d'astigmatisme quel que soit l'angle de champ. Ces systèmes sont beaucoup plus simples que ceux qui visent à obtenir un champ plat. Ils comportent moins d'éléments, ils dispersent moins de lumière nuisible, et leur précision est remarquable. Or ces systèmes produisent tous un champ courbé. Le cinéma et la télévision font un grand usage des lentilles grand angle à champ plat, mais celles-ci souffrent de nombreux inconvénients. On réclamera tôt ou tard de meilleures lentilles. Or les meilleures lentilles comportent des éléments sphériques et concentriques, et leur champ est courbé. Les cinéastes et les photographes amoureux de leur art ne sont pas nécessairement amoureux de l'optique. S'ils connaissaient les enjeux, ils exigeraient des caméras à champ courbé. |
![]()
LES « LENTILLES À MIROIRS ».
|
Toutes les lentilles peuvent être remplacées par des miroirs. C'est d'ailleurs nettement préférable avec des pupilles d'entrée relativement grandes, de l'ordre de 100 mm ou plus. C'est donc le cas des télescopes et des téléobjectifs, mais on peut penser que bon nombre de caméras spécialisées et que certains microscopes y gagneraient aussi. Évidemment ces appareils produisent un champ courbé. Voici d'abord comment un seul miroir sphérique peut produire une image remarquable. |
|
|
La « lentille à miroir » Schmidt à miroir plan perforé.
|
Cet appareil est réversible, à la manière des lentilles, et il peut donc s'agir d'un microscope, d'une caméra pour macrophotographie, ou encore d'un télescope-téléobjectif. Son angle de champ est limité, mais sa précision est remarquable. Il est peu connu, justement parce que sa structure est concentrique et qu'il produit un champ courbé. En tant que microscope il serait très petit. En tant que téléobjectif il serait plus compact que le Schmidt original parce que le miroir perforé a pour effet de rapprocher la pupille de Schmidt du miroir concave. Ce miroir doit être parfaitement plan car autrement il provoque de l'astigmatisme. La pupille de Schmidt est représentée ci-dessus par un cercle. Elle est située au centre de courbure du miroir concave, qui est sphérique, et elle doit donc être munie d'un correcteur d'aberration de sphéricité : Schmidt, Maksutov, Bouwers, Richter-Slevogt, Houghton, etc. À mon avis, c'est le Bouwers concentrique qui produit les images les plus précises, à la condition que l'aberration chromatique et l'aberration de sphéricité résiduelle soient corrigées sur la pupille de Schmidt par le doublet plano-plano achromatique de Richter et Slevogt. Ce dernier est neutre pour la couleur médiane, généralement le vert. J'ai parlé plus haut d'un double Bouwers rempli d'un gaz comprimé. S'il était réalisable, il serait sans doute supérieur au correcteur de Schmidt pour un très grand angle de champ. Un téléobjectif très précis. Un appareil de ce genre, mais inversé, devient le téléobjectif montré ci-dessous. On peut imaginer par exemple un modèle muni d'un miroir ƒ/ 2 de 200 mm. Il utiliserait deux tubes longs de 40 à 60 cm et faisant un angle de 45° environ. Il serait donc relativement plus encombrant que le Schmidt-Cassegrain équivalent, mais il serait nettement supérieur. Sa précision atteindrait facilement la tache d'Airy, qui vaut alors 0,0026 mm. Ce système permettra de photographier beaucoup mieux des scènes éloignées, des oiseaux ou des insectes à la surface de l'eau, par exemple. À mon sens, il est évident qu'un jour les téléobjectifs à lentilles disparaîtront pour faire place à des systèmes à miroir. Il en existe de nombreux modèles. |
|
|
Le télescope de Schmidt en version « repliée ».
|
La perforation du miroir plan peut être très faible, de l'ordre de 12 % du diamètre avec une pupille de 200 mm, et beaucoup moins encore si l'appareil est plus grand. Ce téléobjectif pourra un jour produire environ 50 mégapixels sur une surface électronique concave (R = 40 cm) de 18 x 18 mm. Ceci signifie qu'il sera aussi possible de produire des téléobjectifs beaucoup plus petits, et néanmoins étonnamment précis. Une obstruction très faible n'affecte pas la tache d'Airy de manière perceptible, alors que celle du secondaire des Cassegrain utilisés à l'heure actuelle dépasse souvent 33 %, ce qui est très dommageable. Ce secondaire intercepte une partie de la lumière inutilement et il agrandit l'image, ce qui ne permet pas d'enregistrer autant de pixels. Les fabricants de ces Schmidt-Cassegrain prétendent que leur rendement atteint la précision de la tache d'Airy mais ceux qui sont en mesure de les analyser à l'ordinateur vous diront que c'est un mensonge pur et simple. C'est à cause de l'obstruction, mais c'est aussi à cause de la position du correcteur, qui n'est pas au centre de courbure du miroir. Il faut alors compenser en polissant une conique sur le primaire ou le secondaire, sinon les deux, ce qui ne peut en aucun cas annuler complètement les aberrations en périphérie. Cette conique n'est jamais parfaite et elle conduit à d'autres imprécisions. Pire encore, dans le but de raccourcir l'appareil, ces fabricants utilisent un primaire très fortement courbé. Il faut alors un correcteur plus puissant, ce qui accentue encore ces aberrations. Le télescope ou microscope de Schwarzschild. Voici un appareil merveilleux, et pourtant très peu connu : |
|
|
La "lentille à miroirs" sans aberrations de Karl Schwarzschild (1905).
Peu importe le grandissement choisi, le rayon de courbure du foyer court vaut constamment 80% de celui du miroir convexe.
J'ai ajouté une pupille d'entrée au centre de courbure des miroirs, qui sont tous les deux sphériques (contre toute attente).
En effet, Schwarzschild était décédé à l'époque de la découverte de cette pupille par Bernhard Schmidt, soit vers 1930.
Cette configuration permet d'agrandir ou de réduire l'image d'un objet selon le foyer choisi.
S'il est fait très grand, cet appareil peut produire des milliards de pixels, à ne plus que savoir en faire !
|
Cet appareil présente des caractéristiques tout à fait remarquables. Ses miroirs sont parfaitement sphériques et concentriques, il ne comporte aucun correcteur, et pourtant il est tout à fait exempt d'aberration de sphéricité, de coma et d'astigmatisme. Évidemment, le champ des deux foyers est également sphérique, ce qui élimine toute distorsion. C'est une invention de l'astronome Karl Schwarzschild, qui souhaitait l'utiliser comme télescope (1905). Il a vite compris qu'il serait beaucoup trop encombrant, car il faut alors inverser le trajet des rayons. Dans ce cas le miroir concave devient le miroir secondaire, et il doit être quatre fois plus grand que le primaire. Schwarzschild était un mathématicien remarquable. On lui doit aussi la constante et les formules qui permettent de calculer la conique des miroirs de télescopes. Il a donné la formule du rayon critique qui mène à la formation des trous noirs. Il a aussi inventé un Cassegrain à miroir secondaire concave sans coma. Il ignorait que cet appareil pouvait aussi être libre d'astigmatisme, ce qu'André Couder a démontré peu après. Schwarzschild ne connaissait pas la pupille de Schmidt, découverte par Bernhard Schmidt vers 1930. La version Schmidt-Cassegrain sans correcteur montrée ci-dessus est donc une invention récente, mais je n'ai jamais pu en retrouver la moindre trace. Il s'agit donc encore une fois d'un appareil que j'ai dû réinventer. Il peut être utilisé aussi bien dans une caméra que dans un microscope, car il est parfaitement réversible. En version apodisée et sans obstruction (voir plus loin) il devrait produire des images d'un contraste inégalé puisqu'il n'y a pas de lentille en verre optique ni d'obstruction. C'est évident : il n'y a aucun reflet nuisible. Ici le grandissement vaut 6 ou 0,167 selon le foyer, le rapport entre le rayon de courbure des miroirs vaut 3,689 et le foyer secondaire (qui est interne à plus faible grandissement) est bien dégagé au delà de la perforation du miroir concave. Le taux d'obstruction vaut ici 35% et il augmente jusqu'à 45% selon le grandissement. Celui-ci varie selon le rapport des rayons de courbure des deux miroirs. Le foyer secondaire atteint l'infini si ce rapport vaut 2,618 selon la version originale de Schwarzschild. D'une manière remarquable, le rapport de la distance L entre le foyer primaire et le centre de courbure d'une part, et du rayon de courbure R du miroir convexe d'autre part, correspond à une constante. Sauf pour des poussières, cette constante ne varie jamais quelle que soit la configuration : L / R = 0,8 Cet appareil ne permet donc pas de varier le grandissement selon les formules de Descartes. Il n'est pas possible non plus d'y arriver en modifiant la distance des miroirs. Mais puisque le miroir convexe est très petit on peut en placer trois ou quatre sur une tourelle pour remédier à ce problème, ce dispositif étant d'ailleurs chose courante sur la plupart des microscopes. La courbure de champ est sujette aux mêmes particularités que dans le cas de la lentille Oeil d'Aigle, comme on l'a vu plus haut. L'un des rares appareils à miroirs à la fois sans obstruction et sans aberrations. Les Cassegrain concentriques présentent généralement une forte obstruction (35% ci-dessus) à cause du miroir secondaire, ce qui disperse beaucoup de lumière dans le premier anneau de la tache d'Airy. Ce défaut est souvent sans conséquences car l'appareil peut livrer une image d'autant plus grande que ses proportions sont grandes. Ce n'est pas le cas avec une lentille. Ainsi, le nombre de taches d'Airy peut dépasser de loin le nombre de pixels qu'on peut recueillir, et il importe peu qu'ils soient plus ou moins amochés. Toutefois, parce que ses éléments sont sphériques, ce Schwarzschild est le seul appareil qui puisse être utilisé sans problèmes en version Forster-Fritch (1876) dite Brachyt. Il est très rare que des appareils à miroirs ne présentent aucune obstruction sans qu'il n'en résulte des aberrations. Le Schiefspiegler d'Anton Kutter en est un bon exemple. Ici au contraire la tache d'Airy sera intacte. Il s'agit de désaxer les miroirs de manière à ce que le secondaire n'intercepte plus le faisceau lumineux. Le diamètre de ce faisceau s'en trouve réduit, ce qui conduit à des systèmes moins lumineux. Toutefois il existe de nombreuses situations où cette configuration est avantageuse. On peut en particulier en tirer un microscope stéréoscopique sans obstruction en découpant deux ouvertures circulaires distinctes de part et d'autre de la pupille de Schmidt. Un miroir Mangin grand angle sans aberrations ? À ma connaissance, aucun ouvrage ne fait mention d'un miroir Mangin sphérique achromatique qui soit aussi exempt d'aberration de sphéricité, de coma et d'astigmatisme. Sauf erreur, ce serait pourtant le cas du modèle montré ci-dessous, qui pourrait donc être l'une de mes inventions. Il devrait être remarquablement précis grâce à la pupille de Schmidt : |
|
|
Le miroir Schmidt-Mangin grand angle sans aberrations.
|
Je n'ai évidemment pas pu le construire, mais le programme que j'ai écrit pour le vérifier le donne étonnamment précis. Il se pourrait que mon programme comporte une erreur, mais d'après mon expérience toute erreur dans un programme produit généralement des résultats catastrophiques. Quoi qu'il en soit, j'ai des plans d'autres appareils à miroir de ce genre qui ne sont pas de type Mangin. Le scanner. Les habitués auront vu tout de suite qu'il ne serait pas possible de placer une surface photosensible à l'intérieur de cet appareil, car elle intercepterait toute la lumière. Par contre ce système peut devenir remarquablement performant en termes de pixels si l'image est balayée par un scanner très étroit. Un tel scanner produit une projection cylindrique s'il pivote sur le centre de courbure, même s'il est courbé de manière à respecter la courbure de champ. La pupille d'entrée peut pivoter sur le centre de courbure en même temps que le scanner, et l'ensemble peut alors couvrir un angle de champ dépassant largement 90°. Pour tout dire, le nombre de pixels est pratiquement illimité et il dépend du diamètre de la pupille d'entrée, avec une limite tout de même. On peut donc envisager une scène grandiose (par exemple une vue du Grand Cañon) affichée sur un grand écran cylindrique, et faite de milliards de pixels. Il serait possible d'agrandir un détail et de le voir avec une précision étonnante. C'est impensable aujourd'hui, mais ce sera peut-être normal dans un siècle ou deux. |
![]()
|
Le scanner triomphera-t-il un jour ? Un scanner courbé associé à une bande étroite taillée dans un miroir sphérique, ou à une lentille concentrique, produit aussi une projection cylindrique. La largeur de la caméra peut être inférieure à 5 mm. Le balayage peut se faire à l'aide d'un petit miroir plan rotatif. On peut aussi faire tourner la caméra toute entière autour de sa pupille. Pour le cinéma, on peut même faire tourner jusqu'à 25 de ces caméras à raison d'un tour par seconde autour d'une même pupille virtuelle centrale, obligatoirement en nombre impair. Un tel système sur pied permet d'enregistrer 25 images à la seconde et de couvrir n'importe quel angle de champ, jusqu'à 360°.L'intérêt de ce procédé repose sur le fait que plusieurs scanners peuvent balayer l'image simultanément, mais à des endroits différents. De cette manière leur vitesse de balayage serait considérablement réduite et l'écran de la télévision ou du cinéma ne devrait rafraîchir les pixels que progressivement. Il pourrait en résulter une distorsion, en général peu nuisible, par exemple si une voiture devait se déplacer dans le même sens que le scanner. Il se peut qu'on arrive un jour à améliorer la sensibilité de ces scanners à un point tel que le cinéma n'utiliserait rien d'autre. On pourra éventuellement disposer un certain nombre de cellules dans le même scanner, les unes à côté des autres, sur une bande relativement étroite. Le problème consistera à transférer les charges de l'une à l'autre de manière à immobiliser l'image électroniquement. Alors leur sensibilité serait bien meilleure. On peut consulter l'ouvrage « Optique des Miroirs » à la Bibliothèque Nationale du Québec ou du Canada. Il n'est plus disponible, personne n'ayant manifesté le désir d'en posséder un exemplaire. Les deux copies transmises à la Bibliothèque Nationale de France ont apparemment atterri dans la corbeille. Optique des Miroirs, © Gabriel Lafrenière, juin 2002. ISBN 2-9806972-3-0 Manifestement, les oiseaux rares dans mon genre qui refusent de voler en essaim avec les autres sont en voie d'extinction. Mais puisque vous êtes parvenu à ces lignes, tout n'est pas perdu. Je suis parfaitement conscient que ceux qui sortent des sentiers battus innovent parfois mais qu'ils s'égarent le plus souvent. C'est pourquoi vous seriez aimable de me signaler les erreurs à l'adresse suivante : En terminant. Je vous rappelle que la matière est faite d'ondes et que vous devriez jeter un coup d'œil à la page d'accueil. Vous pourrez examiner le prototype de cette onde stationnaire qu'est l'électron. Croyez-moi, cette onde est une splendeur. Elle se conforme aux transformations de Lorentz d'une manière tout à fait remarquable. On en conclut que si la matière est faite d'ondes stationnaires, elle doit se contracter comme Lorentz l'a montré. Ainsi, contrairement à ce qu'on croit depuis 100 ans, l'éther existe et la matière subit réellement ces transformations. Si vous connaissez bien l'optique et les ondes en particulier, vous devriez vous rendre compte qu'il s'agit d'un fait nouveau et que la théorie de la Relativité peut désormais s'expliquer très facilement. La Relativité se calcule selon Lorentz et non selon Einstein, par des moyens élémentaires. Ce n'est plus une doctrine mystérieuse hors de portée de notre compréhension. |
|
Gabriel LaFrenière, Bois-des-Filion en Québec. Sur l'Internet depuis septembre 2002. Dernière mise à jour le 3 novembre 2009. Page d'accueil : La matière est faite d'ondes. Courrier électronique : veuillez consulter cet avis. La théorie de l'Absolu, © Luc Lafrenière, mai 2000. La matière est faite d'ondes, © Gabriel Lafrenière, juin 2002. Optique des miroirs, © Gabriel Lafrenière, juillet 2001. ISBN 2-9806972-2-2 |