Le blog.

Le 19 août 2011.

LA DIFFRACTION DE FRESNEL

Le programme sur la tache d'Airy (voir plus loin) à peine modifié me permet maintenant de montrer également la diffraction de Fresnel, qu'on obtient avec une source plane circulaire équiphasée (batterie d'émetteurs, laser, sténopé, etc.). On sait que ce phénomène porte plutôt le nom de "diffraction de Fraunhofer" si la distance est suffisamment grande pour que la tache d'Airy apparaisse (à droite ci-dessous).

Cliquez sur l'image pour obtenir la version pleine grandeur (1920 x 1280)

La partie supérieure montre l'énergie, qui vaut le carré de l'amplitude.

En-dessous, l'amplitude permet de montrer qu'il se produit des variations de phase surprenantes, en particulier sur l'axe.

Fresnel avait noté que ce phénomène dépendait d'un entier n, appelé depuis le "nombre de Fresnel". Il avait trouvé que la distance des zones alternativement claires (avec n impair) et sombres (avec n pair) observées sur l'axe était donnée par l'équation suivante:

distance = rayon² / (n * lambda)

Sur l'axe, la luminosité est donc périodiquement réduite à zéro après avoir passé par un maximum, toujours le même, ce qui est tout à fait remarquable. Si elle est à zéro, c'est que la somme de toutes les ondelettes de Huygens est nulle: les interférences sont totalement destructives. Mais si au contraire elle atteint un maximum, ce n'est pas parce qu'elles sont totalement additives: c'est plutôt parce que les ondelettes provenant de la périphérie du disque émetteur sont en phase avec la somme de tout le reste du disque. Ce n'est qu'à l'infini que les interférences sont totalement constructives (diffraction de Fraunhofer), et Fresnel avait donc raison de dire que "ce sont les bords qui diffractent".

J'ai découvert que le nombre de zones, qu'elles soient claires ou sombres, est égal au nombre de longueurs d'ondes qu'il y a dans le rayon de la source. J'avais obtenu des résultats similaires en langage QuickBasic il y a plus de dix ans. J'avais constaté et signalé à cette époque que l'équation donnée par Augustin Fresnel était inexacte quand la longueur d'onde n'était plus négligeable devant le rayon de la source. Mais le programme actuel écrit en langage C étant beaucoup plus efficace, j'ai pu établir que la distance calculée ci-dessus selon Fresnel doit être réduite d'une valeur qui varie également selon le nombre de Fresnel:

correction = 47 * n * lambda / rayon.

La constante 47 ci-dessus n'est qu'une approximation mais elle est suffisamment précise pour que le programme puisse repérer les points d'énergie minimum et maximum sans la moindre défaillance, comme le montrent les images ci-dessus. Cette correction n'est requise que si la longueur d'onde n'est pas négligeable devant le rayon de la source. Ce n'est donc pas très utile en optique, mais il faut insister ici encore une fois avec la plus grande énergie (comme dans le cas de la tache d'Airy ci-dessous) sur le fait que ce phénomène peut aussi être reproduit à l'aide du son.

Il existe donc une "diffraction de Fresnel acoustique", identique en tous points à ce que montrent les images ci-dessus. On l'obtiendrait par exemple avec une plaque circulaire de 48 cm de rayon (soit près d'un mètre de diamètre) sur laquelle seraient répartis uniformément 800 petits haut-parleurs de 3 cm alimentés à la même source et émettant sur une longueur d'onde de 6 cm. Le programme montre en effet que l'espacement entre les haut-parleurs peut difficilement dépasser une demi-longueur d'onde. À partir de ce point, des anomalies commencent à apparaître.

Il est donc remarquable que le son puisse se transmettre ainsi en ligne droite sans faiblir avant que le nombre de Fresnel n'atteigne 1, après quoi seulement il obéit à la règle du carré de la distance tout en conservant un angle de divergence très étroit. On peut évidemment faire beaucoup mieux au moyen d'une source plus grande, ce qui éloigne encore cette distance et réduit l'angle de divergence. On peut également émettre dans les ultrasons, ce qui revient au même mais réduit l'échelle. On pourrait ainsi créer un "rayon sonore" semblable en tous points à un rayon laser. Il serait capable d'aller porter environ 80% de toute l'énergie émise à la source jusqu'à des kilomètres, et toujours à l'intérieur d'un diamètre inférieur à celui de la source!

Le sténopé.

Bien évidemment, le sténopé étant fondamentalement une source lumineuse circulaire plane équiphasée, un point lumineux suffisamment éloigné y produira un faisceau semblable à celui montré plus haut. J'avais autrefois manifesté une nette préférence pour une distance correspondant à un nombre n (non entier) de 0,61 pour profiter du fait qu'à cette distance, la tache d'Airy est beaucoup plus nette qu'au point n = 1. C'est à l'extrême droite de l'image montrée ci-dessous.

À cette époque, on faisait miroiter le fait que les photosites CCD devenaient de plus en plus efficaces et moins vulnérables au bruit de fond. Mais aujourd'hui, il devient clair qu'on a atteint une limite infranchissable. Je dois donc me résigner à admettre que la distance idéale pour situer la pseudo-focale du sténopé correspond au point n = 1, c'est à dire là où l'on obtient le dernier maximum de luminosité. Elle vaut donc très simplement, en millimètres:

pseudo-focale du sténopé = rayon² / 0,00055

Le diagramme présenté ci-dessous n'est pas à l'échelle afin de mieux observer les variations de luminosité à l'intérieur du faisceau lumineux. En effet, si le rayon de la source en termes de longueurs d'onde augmente, la structure générale de la diffraction de Fresnel n'est pas modifiée. Par contre, elle s'en trouve étirée selon le carré du rayon comme la formule ci-dessus l'indique.

Le point n = 1 qui détermine la pseudo-focale du sténopé se situe vers le deuxième tiers de ce diagramme.

Il faut se résigner à ce compromis même si la tache d'Airy est plus nette à l'extrême droite.

Cliquez sur l'image pour obtenir la version pleine grandeur (5000 x 640 pixels).

Normalement, le rayon du trou du sténopé est de 0,25 mm, de sorte que sa focale devrait être d'environ 110 ou 115 mm (0,00055 mm est la longueur d'onde de la lumière verte, la plus visible). Un trou d'un millimètre de diamètre exigerait une focale de 460 mm, donc impraticable, mais sa résolution serait meilleure. D'ailleurs, même une pupille d'entrée d'un millimètre représente un seuil minimum qu'il vaut mieux éviter. Le diamètre de la pupille de notre oeil en plein jour (environ 2 mm) est en effet nettement préférable à cause de la résolution qu'on peut en tirer, même si ce choix a pour effet de réduire quelque peu la profondeur de champ.

Le sténopé électronique.

Mais la photographie électronique a changé la donne en ce qui concerne le sténopé, qui n'a donc pas dit son dernier mot. Le point important, c'est que les dimensions des photosites dans un sténopé électronique devront être beaucoup plus grandes que dans une caméra normale. Cela permettra de surclasser du coup les maigres résultats qu'on obtenait autrefois avec les sels d'argent à cause de l'effet Schwarzschild. Cet effet affecte aussi les capteurs électroniques: ils ne répondent plus, ou ils répondent de manière erratique en-dessous d'un certain seuil. Le seul véritable défaut de cet appareil sera donc d'être incapable de réaliser des instantanés acceptables si l'éclairage laisse à désirer.

Toutefois, le sigle CCD signifie charge coupling device, c'est à dire: dispositif à couplage de charge. Cela signifie qu'on peut quadrupler le rendement énergétique si on couple les photosites par unités de quatre, ce qui a malheureusement aussi pour effet de réduire d'autant la résolution. Mais ce n'est pas le cas pour le sténopé électronique puisqu'on peut compenser en agrandissant toute la surface photosensible. On peut donc à la fois allonger la focale et agrandir la taille des photosites sans pour autant réduire le temps d'exposition.

Rappelons que le rayon du premier zéro d'amplitude de la tache d'Airy vaut:

rayon de la tache d'Airy = 0,61 * lambda / sin (angle d'ouverture)

rayon de la tache d'Airy = 1,22 * lambda * focale / diamètre de la pupille d'entrée

Ainsi donc, une pupille d'un millimètre de diamètre produit à 460 mm une tache d'Airy de 0,62 mm de diamètre. En comparaison, la tache mesure 0,005 mm à l'ouverture plus normale de f/ 4, soit 124 fois moins. Dans un sténopé électronique, il faudra donc agrandir considérablement à la fois les photosites et toute la surface photosensible pour conserver la même résolution. L'appareil coûtera vraisemblablement très cher et peu de gens en voudront à cause de ses grandes dimensions. De plus, cette surface photosensible devra obligatoirement être cylindrique (centrée sur la pupille) pour assurer l'absence de distorsion, du moins sur l'axe le plus long. Bien sûr, cela représente un défi additionnel pour les manufacturiers, mais on obtiendra finalement des résultats absolument uniques en photographie.

Le "sténopé à lentille".

Voilà encore une autre de mes marottes que personne ne semble avoir prise au sérieux. Un sténopé n'est-il pas par définition une caméra sans lentille? En réalité, ce n'est pas si simple. L'avantage majeur du sténopé, c'est qu'il n'a pas de focale réelle, de sorte qu'il devient inutile de régler la mise au point. Il ne possède pas non plus de diaphragme à iris, quoique ça demeure faisable. Mais d'un autre côté, la tache d'Airy est encore à l'état embryonnaire au point n = 1, ce qui produit cet effet de diffusion caractéristique que d'aucuns adorent. Personnellement, je considère que c'est plutôt un défaut, car il existe d'autres moyens d'obtenir cet effet au besoin...

J'affirme donc qu'il est très avantageux d'ajouter au sténopé un système optique très légèrement convergent. Cela permet "d'officialiser" la pseudo-focale pour en faire une focale véritable.

J'avais autrefois présenté les plans d'une caméra relativement légère et compacte faite d'un seul bloc de plastique transparent. Mais on pourrait plus simplement munir le sténopé d'une lentille double ménisque à surfaces presque concentriques et centrées sur la pupille. Cet ensemble ne produit pratiquement pas d'aberrations à faible ouverture. Maintenant que je dispose des outils nécessaires, je peux montrer clairement les avantages de cet ajout somme toute pas bien compliqué à réaliser.

Ci-dessous, on a dans l'image supérieure le diagramme normal de la diffraction de Fresnel. Toutes choses égales d'ailleurs, l'image inférieure montre les changements dramatiques que la lentille apporte au faisceau lumineux. Notez que le foyer de la lentille se situe au point n = 1. On peut en particulier apprécier la luminosité bien supérieure de la tache d'Airy, dont la structure est alors parfaite. Mais le point essentiel, c'est que la surface photosensible peut se situer pratiquement n'importe où dans le dernier tiers de l'image et même bien au-delà, ce qui indique que la profondeur de champ est extrêmement étendue, pour ne pas dire illimitée.

Le faisceau normal du sténopé, dont la luminosité a été normalisée ci-dessus pour fins de comparaison.

Toutes choses étant égales d'ailleurs, on a ajouté ici une faible lentille dont la focale correspond au nombre de Fresnel: n = 1.

Le gain est vraiment remarquable.

Les distances données par le nombre de Fresnel ne correspondent plus puisqu'on a ici, tout simplement, une tache d'Airy.

Cliquez sur ces images pour obtenir la version pleine grandeur (5000 x 640 pixels).

L'ajout d'une lentille présente donc des avantages considérables:

1 - La tache d'Airy est parfaitement formée.

2 - La tache d'Airy est beaucoup plus lumineuse.

3 - La tache d'Airy demeure parfaite sur une très grande distance, ce qui permet de profiter d'un champ cylindrique.

4 - L'effet de diffusion étant éliminé, les photographies sont plus précises et plus contrastées.

5 - La profondeur de champ est encore meilleure à cause de l'hyperfocale, qu'on peut situer à environ deux mètres.

6 - On peut réduire significativement la focale pour obtenir un appareil plus compact.

7 - La lentille obture le trou, ce qui protège la surface photosensible des intempéries et des poussières.

Avec une pupille de 2 millimètres, la pseudo-focale du sténopé devrait normalement se situer à pas moins de 1,8 mètres. Bien sûr, c'est impensable. Mais heureusement, on peut réduire de beaucoup la focale du sténopé à lentille: 150 mm semble un bon compromis avec une pupille de 2 mm de diamètre. Cela correspond à une ouverture relative de f/ 75, et donc à une tache d'Airy mesurant 0,1 mm. Des photosites aussi grands seront bien plus fiables et précis. Si on considère la limite de Dawes, une telle caméra produira facilement 10 mégapixels sur un grand angle de champ et le boîtier requis pourra donc mesurer environ 20 cm, ce qui ne devrait pas décourager les amateurs de belles photographies.

C'est qu'un sténopé idéal exige une surface photosensible cylindrique afin de produire des images sans distorsion sur l'axe le plus long. De cette manière, des photographies juxtaposées l'une à la suite de l'autre peuvent couvrir tout l'horizon sur 360° sans la moindre anomalie aux points de jonction. Sur l'axe le plus court, normalement vertical, le champ est rectiligne et non pas courbé. Il faut donc s'en remettre à la grande profondeur de champ pour éviter que des flous n'y apparaissent. On sait qu'en principe, cela produit une projection dite cylindrique; mais celle-ci sera annulée de facto lorsqu'on admirera la photographie car tous les écrans, qu'ils soient plats ou cylindriques, sont eux aussi rectilignes sur l'axe vertical. C'est pourquoi ces images devraient être visionnées sur un écran cylindrique pour supprimer totalement la distorsion. Il vous faudra vraiment en faire l'expérience pour réaliser qu'un tel écran, surtout s'il est relativement large, donc enveloppant, procure une sensation de "présence" extraordinaire. Les images en trois dimensions y seront donc encore plus spectaculaires.

Ainsi donc, l'ajout d'une lentille est très avantageux. Le seul problème, c'est qu'il faut conserver une ouverture relative très élevée d'au moins f/ 75 pour qu'il soit possible d'annuler totalement la distorsion. Pour le reste, on ne sacrifie en rien les avantages du sténopé, qui vont dans le sens de la simplicité et de la perfection. Tout y est: très grande profondeur de champ, grand angle de champ, pas de distorsion, pas de mise au point, pas de diaphragme à iris, etc., de sorte que l'appareil ainsi modifié mérite de conserver son nom.

Le sténopé ne sera jamais la caméra idéale à cause de sa grande taille.

Mais l'avènement de la photographie 3-D électronique donne à penser qu'il faudra oser un jour fabriquer des caméras à surfaces photosensibles entièrement sphériques. C'est que la courbure de champ n'est pas une aberration. Je le répète ici, Seidel a fait erreur. Je l'ai toujours affirmé avec la plus grande énergie, envers et contre tous:

"La véritable aberration, c'est d'avoir cru tout ce temps que la courbure de champ était une aberration".

J'ai d'ailleurs établi les spécifications complètes d'une lentille que j'ai appelée "Oeil d'Aigle", et dont la surface photosensible est sphérique. Avec une pupille de 40 mm, qui garantit une grande luminosité au besoin, c'est à la fois un puissant téléobjectif et une lentille grand angle capable de produire plus de cent mégapixels. C'est une lentille absolument sans aberrations: sans aberration chromatique, sans aberration de sphéricité, sans coma, sans astigmatisme et, bien évidemment, sans distorsion. La lentille "Oeil d'Aigle" a de l'avenir! Considérant toutes ces qualités, ce qui semble impraticable à l'heure actuelle deviendra forcément la norme dans un futur éloigné. Au contraire des sténopés, ces caméras du futur seront vraiment minuscules et elles produiront néanmoins des images d'une très grande qualité.

Le 8 août 2011.

Lentement mais sûrement, je continue d'apprivoiser le langage de programmation C. Dans le but d'en finir avec la tache d'Airy, j'ai entrepris de traduire en C un ancien programme écrit en QuickBasic, tout en l'améliorant. Ce programme fait la sommation des "ondelettes de Huygens" produites par des sources réparties uniformément sur la surface d'une calotte sphérique. C'est l'équivalent d'un calcul intégral: il correspond en effet aux "intégrales de Fresnel", basées sur le principe de Fresnel, ce dernier n'étant qu'une formulation un peu plus précise du principe de Huygens.

L'expérience montre qu'il n'est pas nécessaire d'échantillonner des millions d'ondelettes: si l'espacement entre chaque source est d'une demi-longueur d'onde, c'est bien suffisant. Bien entendu, c'est l'ordinateur qui se charge du travail, de sorte qu'on n'a pas à se soucier des "conditions aux limites" ni des autres contraintes propres au calcul intégral. Bref, il s'agit purement et simplement d'une addition.

Je dois préciser que j'avais également mis au point une méthode impliquant la sommation d'un nombre très restreint d'arcs de cercles (une centaine suffit), ce qui est bien plus rapide. Toutefois, ce programme étant destiné aux opticiens et acousticiens qui voudront se familiariser avec la méthode, j'ai retenu la plus simple. Le problème principal consistait à répartir les sources sur la surface sphérique le plus uniformément possible. Vous verrez que le calcul complet ne requiert que 17 lignes de programme faciles à comprendre et à modifier selon les besoins.

J'avais signalé il y a longtemps que le rayon du disque ne correspondait pas nécessairement au chiffre d'Airy, c'est à dire: 1,22 lambda (il vaut normalement 1,22 fois l'ouverture relative, en longueurs d'onde). En réalité, si l'on ouvre l'angle d'ouverture jusqu'à 90°, ce rayon finit par atteindre exactement une demi-longueur d'onde. Si cet angle correspond à une sphère complète, on obtient tout simplement des ondes stationnaires sphériques, dont le noyau central mesure également une demi-longueur d'onde de rayon. Mais puisque je dispose maintenant d'outils formidables, j'ai pu récemment trouver la formule exacte. Si P (phi) est l'angle d'ouverture et L (lambda) la longueur d'onde, le rayon R du disque d'Airy est donné par:

R = L (0,61 – (0,11 (1 – cos P)^2)) / sin P

Cette formule n'est qu'une approximation, mais elle s'avère raisonnablement juste. Si l'angle d'ouverture dépasse 90°, le rayon demeure stable à 0,5 fois la longueur d'onde. Il faut noter que 0,61 correspond à la moitié du chiffre d'Airy mentionné ci-dessus. La correction agit sur la différence entre 0,61 et 0,5, soit 0,11. Mais elle est inutile si l'ouverture angulaire est inférieure à 30° (ou si l'ouverture relative est supérieure ƒ/ 1), de sorte que la formule requise est alors bien plus simple:

R = 0,61 L / sin P

Ce programme a ceci de particulier qu'il peut reproduire le phénomène de la tache d'Airy quand la longueur d'onde n'est plus négligeable devant la focale. Ce n'est pas très utile en optique, mais il faut insister ici avec la plus grande énergie sur le fait que ce phénomène peut être reproduit également en acoustique et en électronique. Peu de gens le savent, mais il est très possible de réaliser une tache d'Airy sonore ou électromagnétique. Alors elle présentera exactement les mêmes caractéristiques. On remarque que dans ce cas, la symétrie normalement parfaite entre les parties avant et arrière du plan focal est compromise. Il semble bien que ce soit une autre de mes découvertes. Je pense que je suis également le premier à signaler que dans ce cas, la surface focale de la tache d'Airy est sphérique: son rayon de courbure correspond à la focale.

Voici donc le programme en question, ainsi qu'un exemple des images qu'il est capable de produire. Ceux qui connaissent bien le phénomène de la tache d'Airy s'y reconnaîtront facilement:

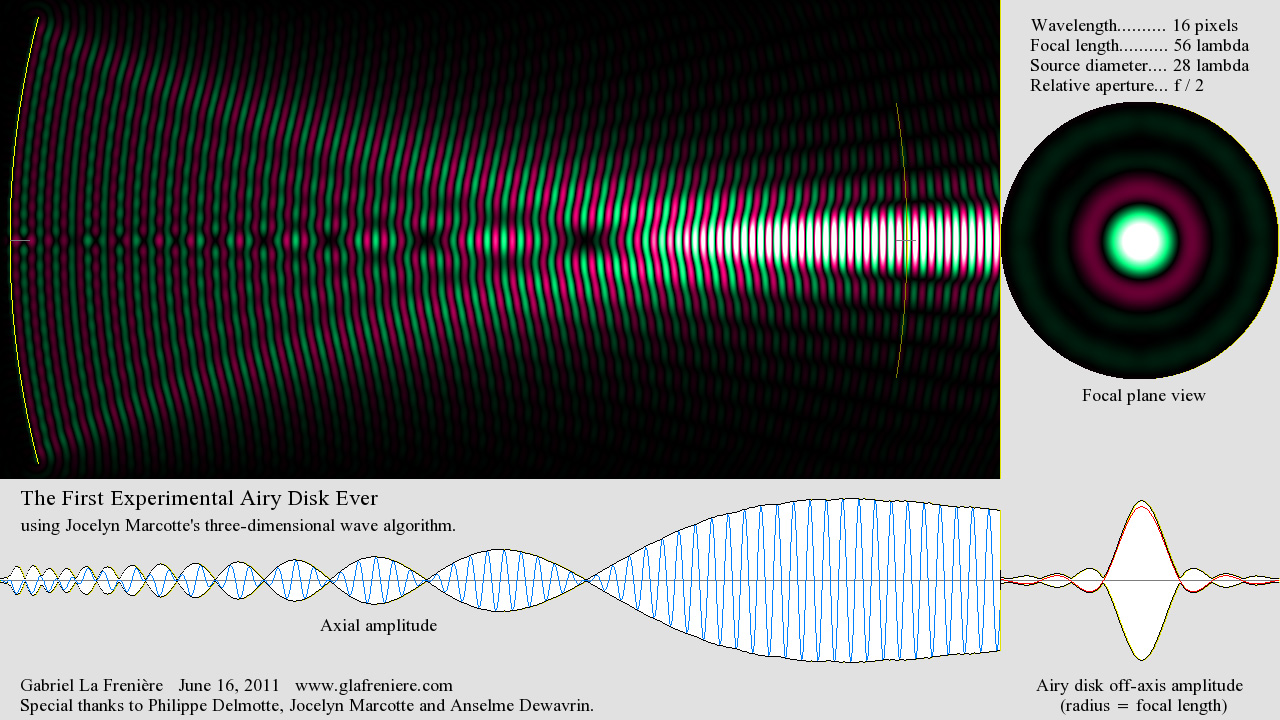
M. Jocelyn Marcotte a mis au point un algorithme à trois dimensions dont l'ingénierie est absolument parfaite et garantit une propagation uniforme dans toutes les directions avec une précision stupéfiante. Vous comprendrez néanmoins que votre ordinateur mettra beaucoup de temps à produire une image, car il lui faudra effectuer des milliards et des milliards de calculs. Il doit en effet composer avec un espace à trois dimensions (1000 x 480 x 480) contenant plus de 230 millions de cellules individuelles de la taille d'un pixel et entourées chacune de 26 voisines dont il faut évaluer l'influence relative.

Si des amateurs comme moi arrivent à faire mieux que les professionnels, c'est la preuve que rien ne va plus de nos jours dans le monde de la physique... Comme je l'ai écrit ci-dessous, les opticiens et les acousticiens en général manquent sérieusement de vision et d'envergure. Je ne comprends vraiment pas ce qui les incite à ignorer ce laboratoire de l'avenir. Le mépris qu'ils manifestent pour ce que nous faisons ne les honore guère, mais c'est surtout leur inconscience qui étonne. Parce qu'ils ne disposent d'aucun outil moderne et efficace, ils ne sont même pas en mesure de vérifier par eux-mêmes le bien-fondé de mes hypothèses, particulièrement en ce qui concerne l'optique du mouvement, c'est à dire la Relativité.

D'ailleurs, grâce à ce nouvel outil désormais tout à fait fonctionnel, je serai en mesure de vous présenter en images saisissantes tout ce qu'il faut savoir sur la Relativité. Et ce sera sans toutes ces balivernes à propos d'une prétendue "transformation de l'espace-temps"...

Croyez-moi, ça n'est pas si compliqué que ça en a l'air. C'est dans la simplicité qu'on comprend le mieux. Il suffit de bien explorer le sujet au préalable, avec toute la rigueur nécessaire. Descartes ne disait-il pas que toute vérité devient alors fondamentalement évidente?

Le 7 juin 2011.

Voici deux programmes qui montrent le fonctionnement des algorithmes de MM. Philippe Delmotte et Jocelyn Marcotte, qui permettent à des ondes de se propager dans un "médium virtuel" :

11-05_Delmotte_Wave_Algorithm.zip

11-05_Marcotte_Wave_Algorithm.zip

Cet autre programme indique comment éliminer les réflexions ennuyeuses à l'aide d'une zone d'affaiblissement :

11-06_Damping_Area.zip

M. Marcotte et moi avons également retravaillé la version tridimensionnelle de son algorithme, qui convient particulièrement au langage C. Grâce à une utilisation judicieuse des pointeurs, ce véritable génie (je n'exagère pas, je vous assure) a réussi à éliminer l'un des trois tableaux de variables, qui consomment énormément de mémoire en mode 3-D. Cela permet d'agrandir sensiblement les dimensions de notre "cube d'éther", de sorte que nous pourrons enfin expérimenter toutes sortes de phénomènes ondulatoires. Je travaille présentement sur la diffraction de Fresnel et sur la tache d'Airy, bien sûr en 3-D. Et ce n'est qu'un début. Voici donc ma première expérience réalisée dans un médium à trois dimensions:

11-06_3D_Spherical_Standing_Waves.zip

11-06_3D_Spherical_Standing_Waves.mkv

Les ondes stationnaires sphériques.

Ceci n'est qu'un aperçu de ce que notre « médium virtuel » peut faire.

C'est un véritable laboratoire qui nous permettra de vérifier expérimentalement tous les phénomènes ondulatoires.

J'écris maintenant mes programmes en langage C puisque c'est le plus connu et surtout le plus efficace. Vous trouverez les indications nécessaires au début du code source si vous choisissez de les compiler vous-mêmes sur la plate-forme de votre choix, ce qui est bien évidemment la meilleure chose à faire. Ce code source n'est pas bien long et il tient dans un seul fichier, ce qui devrait vous faciliter les choses.

M. Delmotte avait mis au point son algorithme en juin 2005 mais sa vitesse d'exécution (du moins dans l'algorithme qu'il m'avait proposé au début) était limitée à 0,5 pixel par boucle. Je tiens donc à souligner que c'est M. Delmotte qui, pour autant que je sache, a réussi le premier à mettre au point un algorithme simple et efficace qui ne présente aucun des défauts qui sont présents dans ceux qui existaient précédemment. M. Delmotte insiste sur le fait que si l'on considère chaque point (ou granule ?) d'éther, c'est sa capacité à réagir qui fait toute la différence. Il ajoute:

"Sans cette notion, toute la recherche perd de sa valeur, c'est elle qui expliquera pourquoi les ondes ne se dispersent pas mais restent concentrées pour donner naissance à des "solitons". Chaque point d'éther possède une capacité à réagir qui n'est pas fixe dans le temps et qui dépend directement de l'état d'excitation de l'éther sur les points voisins. La formule qui permet de préserver l'équilibre du milieu tout en permettant de faire des effets de loupes sera la combinaison gagnante."

M. Marcotte a proposé sa propre version, un peu plus simple que celle de M. Delmotte, en janvier 2006. Il avait réussi dès le début à obtenir la vitesse idéale d'un pixel par cycle, même en 3-D, ce qui permet de simplifier énormément la mise en place et le traitement des ondes (il suffit en particulier de tenir compte de la longueur d'onde pour établir la période de l'émetteur). Mais ce n'est que ce mois-ci que j'ai réussi à transposer l'astuce de M. Marcotte dans l'algorithme de M. Delmotte, qui consiste à tenir compte partiellement de l'influence des granules placés en diagonale. Désormais, les ondes avancent à la vitesse d'un pixel par cycle dans les deux cas, ce qui simplifie en outre la mise en place de mes "transformations Alpha". On obtient grâce à elles un effet Doppler absolument parfait en déplaçant l'émetteur tout en tenant compte de l'onde de phase de Louis de Broglie, qui correspond au "temps local" de Lorentz. Il s'agit en fait d'une adaptation des transformations de Lorentz, d'où la simplification c = 1 retenue par Henri Poincaré...

Voilà maintenant six ans que j'ai présenté ce médium virtuel sur l'Internet et que je l'ai proposé à un grand nombre de personnes avec la plus grande insistance par courrier électronique. J'en ai tiré des démonstrations absolument époustouflantes. Et pourtant, il semble bien que personne dans le milieu scientifique ne l'ait encore vraiment adopté pour effectuer des expériences en optique et en acoustique.

Devant de pareils résultats, je dois en venir à la conclusion que les opticiens et les acousticiens en général manquent sérieusement de vision et d'envergure. Je sais, ce n'est pas très correct de parler ainsi; mais pour ce que j'ai à perdre (j'aurai 70 ans l'an prochain), autant y aller de bon cœur. Dois-je vous rappeler que ce médium virtuel est l'outil par excellence pour étudier les ondes, et donc l'optique, l'acoustique, la Relativité et même le fonctionnement intime de la matière? C'est un véritable laboratoire qui permet de montrer exactement comment les ondes se comportent. Alors pourquoi s'en priver?

Par exemple, on peut déjà mettre en évidence de subtiles différences entre la version de M. Delmotte et celle de M. Marcotte. C'est la preuve qu'une onde ne se résume pas à une équation, comme la plupart des mathématiciens (je récidive) semblent le croire. Une onde peut se comporter très différemment selon le médium qui la supporte, et l'on sait déjà que le son en particulier présente des particularités selon la nature des gaz, liquides ou solides dans lesquels il se propage. Il existe aussi des ondes électroniques, les électrons libres d'un métal se comportant comme les "granules" d'un médium très particulier, sachant que ceux-ci se repoussent mutuellement. La période oscille donc entre un maximum et un minimum toujours positifs. Comme c'est le cas du son dans l'air, dont les molécules se repoussent à cause de leurs vibrations dues à la chaleur, ces ondes n'ont pas d'amplitude négative. Elles sont forcément asymétriques et capricieuses à haute intensité. Bref, les algorithmes de MM. Delmotte et Marcotte ne constituent que le point de départ: on pourra en créer d'autres plus complexes (qui tiendront compte de la densité, de la rigidité, etc.) aux propriétés surprenantes.

Il est bien connu en effet que la vitesse des ondes dépend principalement de deux choses: la densité du médium d'une part, qui la ralentit, et sa rigidité d'autre part, qui l'accélère. Il faut aussi savoir que cette vitesse peut varier selon la fréquence, mais aussi selon le taux de compression du médium. Or les ondes stationnaires ont précisément pour effet de comprimer puis de dilater périodiquement ce médium dans les ventres de tension. Simultanément, elles ont pour effet de déplacer les granules de ce médium dans les ventres de courant. Ainsi, lorsque des ondes progressives traversent transversalement des ondes stationnaires, elles en sont forcément affectées: il se produit un "effet de lentille". Pour la même raison, si l'axe est le même, la vitesse de chaque front d'onde doit varier selon qu'il se situe dans la zone dilatée ou comprimée des ventres successifs. Il se trouve que ce peut être l'un ou l'autre, mais pas les deux à la fois. L'onde stationnaire est donc hautement sélective. C'est ce qui me permet de croire que l'électron est fait d'ondes stationnaires sphériques, et qu'il peut subsister indéfiniment par amplification à la seule condition qu'il se trouve dans un milieu où circulent constamment des ondes progressives. Or en se comportant ainsi, l'électron émet des ondes progressives qui iront donc alimenter à leur tour d'autres électrons. C'est pourquoi leur énergie est recyclée indéfiniment.

On peut plus exactement contrôler le comportement des ondes en variant la manière dont son énergie se transmet de proche en proche par l'intermédiaire de "granules". Leur nombre étant limité dans un espace d'une longueur d'onde, ces granules déterminent de toute évidence des effets quantiques que M. Anselme Dewavrin a fort bien analysés en faisant le rapprochement avec la méthode d'Euler. Sachant qu'une onde élémentaire est sinusoïdale, on peut ainsi déterminer le sinus et le cosinus d'un angle avec une grande précision. Qui dit effet quantique dit constante, et c'est pourquoi j'ai proposé de l'appeler (malgré ses protestations) la "constante de Dewavrin"!

Oubliez-donc les équations et observez ce qui se passe. La physique, ce n'est pas l'affaire des mathématiciens. C'est l'affaire des gens qui ont les deux pieds sur terre et qui veulent savoir "comment ça marche"...

Le 13 mai 2011.

Si je n'ai guère modifié ce site dernièrement, ce n'est pas parce que j'ai ralenti mes activités. Je serais en droit de le faire puisque je suis né en 1942. Pourtant, à l'approche de mes 70 ans, je me suis dit que je pourrais présenter de bien meilleures preuves de tout ce que j'avance si j'écrivais mes programmes en langage C.

J'en ai maintenant la preuve : le langage C travaille beaucoup plus vite. Après quelques tâtonnements, et grâce à l'aide précieuse de MM. Anselme Dewavrin et Jocelyn Marcotte, j'arrive déjà à montrer de quelle manière des ondes se propagent. À preuve, ces premiers programmes dont l'exécutable ne fonctionne que sous Windows 7 ou Windows XP. Si vous utilisez une autre plate-forme, vous devrez les compiler vous même, ce qui devrait être relativement facile puisque le code source tient dans un seul fichier :

11-06_3D_Spherical_Standing_Waves.zip

Parabolic_Reflector.zip

Si vous programmez en C, vous savez déjà qu'il est nécessaire de faire appel à des "bibliothèques". J'ai choisi la SDL, qui permet de réaliser des graphiques. Le fichier SDL.dll doit donc être présent avec le fichier exécutable pour que celui-ci puisse démarrer correctement. Pour l'instant, j'utilise l'éditeur Code::Blocks et le compilateur MinGW (GNU GCC). Ce compilateur comporte une option "optimize even more (for speed) [-O2]" qui permet d'accélérer la vitesse d'exécution.

Je me suis également procuré un nouvel ordinateur à quatre processeurs, de sorte que je peux désormais réaliser de courtes séquences vidéo en quelques minutes. Autrefois, il fallait y consacrer des heures. Voici par exemple comment les ondes stationnaires sphériques (donc tridimensionnelles) se comportent:

11-06_3D_Spherical_Standing_Waves.mkv

Je tiens à souligner qu'il s'agit d'une véritable expérience de laboratoire, même si elle a été réalisée dans le médium "virtuel" Delmotte-Marcotte à trois dimensions. Le procédé est simple: on crée des ondes sphériques progressives normales, puis on inverse leur sens de manière à ce qu'elles reviennent au point de départ et interfèrent avec elles-mêmes. Mes calculs établis selon le Principe de Huygens s'en trouvent confirmés. Désormais, on ne pourra plus contester l'existence d'un tel phénomène. Il faudra en prendre acte...

Le 31 mars 2011.

Vous trouverez à la fin de la page sur le Big Bang Relativiste de nouveaux renseignements sur l'hypothèse de l'expansion de l'univers. Bien évidemment, on préfère parler ici de l'éther et non de "l'espace". Mais cela revient au même puisque les galaxies qui s'éloignent de nous peuvent tout aussi bien être considérées au repos comparativement à "l'espace" local.

Si vous vous donnez la peine d'y réfléchir, vous verrez bien que la théorie actuelle sur la constante de Hubble et sur une hypothétique "expansion accélérée" de l'univers est prématurée. Il faudrait d'abord se mettre d'accord sur la manière dont l'expansion de l'univers devrait se dérouler pour provoquer le redshift que nous constatons dans la lumière provenant des galaxies éloignées.

En particulier, il est clair qu'une telle expansion ne peut pas produire d'effet Doppler véritable. De plus, si le médium (ou l'espace) prend de l'expansion, les ondes émises doivent forcément prendre elles aussi de l'expansion en termes de longueur d'onde. Il se produit certainement un "redshift", mais il n'est plus mesurable si l'observateur prend lui-même de l'expansion. Si l'on considère trois observateurs A, B et C, dont la différence de vitesse correspond à la vitesse de la lumière, on peut représenter ce phénomène de la manière suivante:

Les ondes émises dans un univers en expansion demeurent sphériques et concentriques : il n'y a pas d'effet Doppler.

Si tout ce que contient l'univers prend de l'expansion, tout se passe comme si cette expansion n'avait pas lieu.

On peut donc énoncer un "Principe de la relativité de l'expansion", qui se lit comme suit :

Si elle est générale, toute expansion est invérifiable.

Le principe de la relativité de l'expansion.

L'univers n'obéit pas à cette règle puisque nous observons bel et bien un redshift. Celui-ci correspond donc à une anomalie dans l'une des variables impliquées dans le phénomène d'expansion. On pourrait par exemple l'expliquer en supposant que les galaxies elles-mêmes et tous les objets qu'elles contiennent ne sont pas en expansion, ou encore en supposant qu'il s'agit bien d'une expansion accélérée comme le soutient M. Perlmutter.

Mais si on se donne la peine d'y réfléchir, on comprend que la cause de ce redshift pourrait provenir de n'importe quelle autre anomalie.